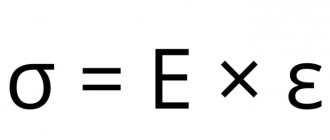The author is a professional tutor, author of textbooks for preparing for the Unified State Exam Igor Vyacheslavovich Yakovlev
Topics of the Unified State Examination codifier: forces in mechanics, elastic force, Hooke's law.
As we know, on the right side of Newton’s second law is the resultant (that is, the vector sum) of all forces applied to the body. Now we have to study the forces of interaction between bodies in mechanics. There are three types: elastic force, gravitational force and friction force. We start with elastic force.
Types of deformation
Deformation is a change in the shape or size of the body.
There are several types of deformation:
- shift;
- torsion;
- bend;
- compression/extension;
Shear deformation occurs when some parts of the body move relative to other parts of the body. If we apply a horizontal force to the top of a cardboard box filled with various objects, we will cause the top of the box to shift relative to its bottom.
Compression or stretching is easy to imagine using the example of a rectangular piece of thin rubber. This deformation is used, for example, in elastic bands for clothing.
Examples of bending and torsion are shown in Figure 1. A plastic ruler deformed by bending is shown in Figure 1. 1a, and in Figure 1b - the same ruler deformed by torsion.
Rice. 1. plastic ruler, deformed by bending – a) and torsion – b)
In a deformable body, forces arise that are of an electromagnetic nature and prevent deformation.
Basic concepts of continuum mechanics
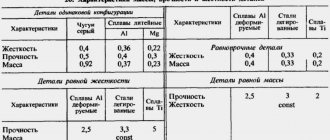
BASIC CONCEPTS OF Continuum MECHANICS Main objects of theoretical mechanics • Material point • Discrete systems of material points • Absolutely rigid bodies Basic objects of continuum mechanics • Gaseous media • Liquid media • Solid deformable bodies Characteristics of continuous media • Homogeneity (heterogeneity) relative to some property • Isotropy ( anisotropy) with respect to some property Types of forces in continuum mechanics • Mass forces act on all elements of a continuum.
Spring stretch
Let's take a closer look at tensile deformation using the example of a spring.
Let's attach a spring to some surface (Fig. 2). The figure on the left shows the initial length \(L_{0}\) of the spring.
Rice. 2. By comparing the length of the free spring with the length of the loaded one, you can find its elongation
Now let's hang a weight on the spring. The spring will have the length \(L\) shown in the figure to the right.
Let's compare the length of the loaded spring with the length of the freely hanging spring.
\[ \large L_{0} + \Delta L = L \]
Let's find the difference (difference) between the lengths of a freely hanging spring and a spring with a load. To do this, subtract the value \(L_{0}\) from both sides of this equation.
\[ \large \boxed{ \Delta L = L — L_{0} }\]
\( L_{0} \left(\text{m} \right) \) – initial length of the spring;
\( L \left(\text{m} \right) \) – final length of the stretched spring;
\( \Delta L \left(\text{m} \right) \) – a piece of length by which the spring was stretched;
The quantity \(\Delta L\) is called the elongation of the spring.
Sometimes relative elongation is calculated. This elongation is often expressed as a decimal fraction. Or a fraction whose denominator is the number 100 - such a fraction is called a percentage.
Note: A ratio is a fraction. Relative means fractional.
\[ \large \boxed{ \frac{\Delta L }{ L_{0}} = \frac{ L — L_{0}}{L_{0} } = \varepsilon } \]
\( \varepsilon \) is the ratio (proportion) of the stretch of the spring to its initial length. It is measured as a percentage and is called relative elongation.
Generalized Hooke's law
Hooke's law usually refers to the linear relationship between strain components and stress components.
Let's take an elementary rectangular parallelepiped with faces parallel to the coordinate axes, loaded with normal stress σх, uniformly distributed over two opposite faces (Fig. 1). In this case, σy = σz = τхy = τхz = τyz = 0.
Rice. 1 Up to the limit of proportionality, the relative elongation is given by the formula where E is the tensile modulus of elasticity.
For steel, E = 2*105 MPa, so the deformations are very small and are measured as a percentage or 1*105 (in strain gauge devices that measure deformations). Elongation of an element in the x-axis direction is accompanied by its narrowing in the transverse direction, determined by the strain components where μ is a constant called the transverse compression ratio or Poisson’s ratio.
Calculation of elastic force
If we stretch a spring by hand, we can notice that the more we stretch the spring, the more it resists.
This means that the elongation of the spring is associated with a force that resists this elongation.
Of course, if the spring is elastic enough to resist. For example, a multi-colored toy spring (Fig. 3), made of plastic, will practically not resist stretching, which doubles its length.
A multi-colored plastic toy spring has little resistance to stretching.
Hooke's law
The English physicist Robert Hooke, who lived in the second half of the 17th century, established that the resistance force of a spring and its elongation are directly proportional. He called the force with which the spring resists deformation \( F_{\text{control}} \) the force of elasticity.
\[ \large \boxed{ F_{\text{control}} = k \cdot \Delta L }\]
This formula was called Hooke's law of elasticity.
\( F_{\text{control}} \left( H \right) \) – elastic force;
\( \Delta L \left(\text{m} \right) \) – spring elongation;
\( \displaystyle k \left(\frac{H}{\text{m}} \right) \) – stiffness (elasticity) coefficient.
What deformations are called small
Hooke's law is used for small elongations (strains).
If the deforming force is removed and the body returns to its original shape (size), then the deformations are called small.
If the body does not return to its original shape, the deformation cannot be called small.
How to calculate the stiffness coefficient
A weight attached to the end of the spring stretches it (Fig. 4). Let's measure the elongation of the spring and create a force equation for the projection of forces on the vertical axis. The weight of the load is directed against the axis, and the elastic force opposing it is directed along the axis.
Rice. 4. The weight of a load suspended on a spring is balanced by the elastic force
Since the forces cancel each other, there is a zero on the right side of the equation.
\[ \large F_{\text{control}} - m \cdot g = 0 \]
Let us substitute the expression for the elastic force into this equation
\[ \large k \cdot \Delta L — m \cdot g = 0 \]
Let's add the weight of the load to both parts and divide by the measured change in length \(\Delta L\) of the spring. We obtain an expression for the stiffness coefficient:
\[ \large \boxed{ k = \frac{ m \cdot g }{\Delta L} }\]
\(g\) is the acceleration of gravity, it is related to the force of gravity.
Hooke's law definition and formula
Ministry of Education of the Autonomous Republic of Crimea Tauride National University named after.
Vernadsky Study of the physical law HOOK'S LAW Completed by: 1st year student of the Faculty of Physics gr.
F-111 Potapov Evgeniy Simferopol-2010 Plan:
- How was the law discovered: based on experimental data or theoretically?
- Examples of using the law and taking into account the effect of the law in practice.
- Statement of the law
- Literature.
- Mathematical expression of the law.
- The connection between what phenomena or quantities is expressed by the law.
- Experienced facts on the basis of which the law was formulated.
- Experiments confirming the validity of the law formulated on the basis of the theory.
The connection between what phenomena or quantities is expressed by the law: Hooke's law connects such phenomena as stress and deformation of a solid body, modulus of elastic force and elongation.
We connect two identical springs
In physics problem books and textbooks for preparing for the Unified State Exam, there are problems in which identical springs are connected in series or in parallel.
Parallel connection of springs
Figure 5a shows a freely hanging spring. Let's load it (Fig. 5b), it will stretch by the amount \(\Delta L\). Let's connect two such springs in parallel and hang a load in the middle of the crossbar (Fig. 5c). The figure shows that a structure of two parallel springs under the action of a load will stretch less than a single such spring.
Rice. 5. Two springs connected in parallel are deformed less than one such spring
Let us compare the stretch of two identical springs connected in parallel with the stretch of one spring. We hang one load weighing \(mg\) from the springs.
One spring:
\[ \large k_{1} \cdot \Delta L = m \cdot g \]
Two parallel springs:
\[ \large k_{\text{parallel}} \cdot \Delta L \cdot \frac{1}{2}= m \cdot g \]
Since the right sides of the equations are the same, the left sides will also be equal:
\[ \large k_{\text{parallel}} \cdot \Delta L \cdot \frac{1}{2}= k_{1} \cdot \Delta L \]
Both sides of the equation contain the value \(\Delta L\). Let's divide both sides of the equation by it:
\[ \large k_{\text{parallel}} \cdot \frac{1}{2}= k_{1} \]
Let's multiply both sides of the resulting equation by the number 2:
\[ \large \boxed{ k_{\text{parallel}} = 2k_{1} } \]
The stiffness coefficient \(k_{\text{parallel}}\) of two springs connected in parallel has doubled compared to one such spring
Series connection of springs
Figure 6a illustrates a free-hanging spring. The loaded spring (Fig. 6b) is stretched to a length \(\Delta L\). Now let's take two such springs and connect them in series. Let's hang a load on these (Fig. 6c) springs.
Practice shows that a structure of two springs connected in series under the action of a load will stretch more than a single spring.
Each spring in the chain is subject to the weight of the load. Under the influence of weight, the spring stretches and transmits this weight further along the chain without changes. He stretches the next spring. And that, in turn, is stretched by the same amount \(\Delta L\).
Note: Under the influence of force, the spring stretches and transmits this tensile force further along the chain without changes
Rice. 6. A system consisting of two identical springs connected in series, more than one spring is deformed
Let's compare the stretch of two identical springs connected in series and the stretch of a single spring. In both cases, we suspend the same load weighing \(mg\) from the springs.
One spring:
\[ \large k_{1} \cdot \Delta L = m \cdot g \]
Two springs in series:
\[ \large k_{\text{last}} \cdot \Delta L \cdot 2 = m \cdot g \]
Since the right sides of the equations are the same, the left sides will also be equal:
\[ \large k_{\text{last}} \cdot \Delta L \cdot 2 = k_{1} \cdot \Delta L \]
Both sides of the equation contain the value \(\Delta L\). Let's divide both sides of the equation by it:
\[ \large k_{\text{last}} \cdot 2 = k_{1} \]
Divide both sides of the resulting equation by the number 2:
\[ \large \boxed{ k_{\text{last}} = \frac{k_{1}}{2} } \]
The stiffness coefficient \(k_{\text{last}}\) of two springs connected in series will be halved compared to one such spring
Potential energy of a compressed or stretched spring
A spring compressed (the left part of Fig. 7) or stretched (the right part of Fig. 7) by a length \(\Delta L\) has the potential to return to its original state and at the same time do work, for example, to move a load. In such cases, physicists say that the spring has potential energy.
Rice. 7. A deformed - compressed or stretched spring has potential energy
This energy depends on the spring constant and on its elongation (or shortening during compression).
The greater the stiffness (elasticity) of the spring, the greater its potential energy. By increasing the elongation of the spring, we obtain an increase in its potential energy according to the quadratic law:
\[ \large \boxed{ E_{p} = \frac{k}{2} \cdot \left( \Delta L \right)^{2} }\]
\( E_{p} \left( \text{J} \right)\) – potential energy of a compressed or stretched spring;
\( \Delta L \left(\text{m} \right) \) – spring elongation;
\( \displaystyle k \left(\frac{H}{\text{m}} \right) \) – coefficient of stiffness (elasticity) of the spring.
Theoretical mechanics and strength of materials
Hooke's law is a basic relationship in mechanics that establishes the relationship between and corresponding to them. The law was discovered in 1660 by an English scientist. After conducting a series of experiments with springs, Hooke noticed that the change in their length is directly proportional to their tensile (compressive) force.
He formalized his observations in the form of a law: “What is the force, so is the elongation.”
The modern formulation of the law differs significantly from the original and depends on the discipline in which effort dependence is considered.
For more information about Hooke's law, watch our video:
In modern physics textbooks, Hooke's Law looks like this:
conclusions
- Elastic bodies are those that resist deformation;
- During deformation, a force arises in elastic bodies, it prevents deformation, it is called the elastic force;
- Deformation is a change in the shape or size of the body;
- There are several types of deformation: bending, torsion, shear, tension/compression;
- The elongation of a spring is the difference between its final and initial lengths;
- A compressed or stretched spring has potential energy (in general, any elastically deformed body has potential energy);
- A system consisting of several identical springs will have a stiffness coefficient different from that of a single spring;
- If the springs are connected in parallel, the stiffness coefficient of the system increases;
- And if you connect the springs in series, the stiffness coefficient of the system will decrease.
9.8. Formulas of generalized Hooke's law
Huber-Mises plasticity hypothesis According to this hypothesis, the transition of a body from an elastic to a plastic state occurs when
will reach some constant value. The question arises: why does the Mises hypothesis, leading to a more complex expression for
, is accepted along with the Saint-Venant hypothesis.
It reaches a maximum at pure shear when