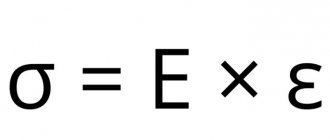History of research into the elasticity of materials
The physical theory of elastic bodies and their behavior under the action of external forces was examined and studied in detail by the 19th century English scientist Thomas Young. However, the concept of elasticity itself was developed back in 1727 by the Swiss mathematician, physicist and philosopher Leonhard Euler, and the first experiments related to the modulus of elasticity were carried out in 1782, that is, 25 years before the work of Thomas Young, by the Venetian mathematician and philosopher Jacopo Ricatti.
The merit of Thomas Young lies in the fact that he gave the theory of elasticity a harmonious modern look, which was subsequently formalized in the form of a simple and then a generalized Hooke's law.
Physical nature of elasticity
Any body consists of atoms, between which forces of attraction and repulsion act. The balance of these forces determines the state and parameters of a substance under given conditions. Atoms of a solid body, when insignificant external forces of tension or compression are applied to them, begin to shift, creating a force opposite in direction and equal in magnitude, which tends to return the atoms to their initial state.
In the process of such displacement of atoms, the energy of the entire system increases. Experiments show that for small deformations the energy is proportional to the square of the magnitude of these deformations. This means that the force, being a derivative with respect to energy, turns out to be proportional to the first power of the magnitude of the deformation, that is, it depends linearly on it. Answering the question of what is the modulus of elasticity, we can say that it is a coefficient of proportionality between the force acting on an atom and the deformation that this force causes. The dimension of Young's modulus coincides with the dimension of pressure (Pascal).
Aluminum production
The main raw material for aluminum production is bauxite containing 32-60% alumina Al2O3. The most important aluminum ores also include alunite and nepheline. Russia has significant reserves of aluminum ores. In addition to bauxite, large deposits of which are located in the Urals and Bashkiria, a rich source of aluminum is nepheline, mined on the Kola Peninsula. A lot of aluminum is also found in deposits in Siberia.
Aluminum is produced from aluminum oxide Al2O3 by the electrolytic method. The aluminum oxide used for this must be sufficiently pure, since impurities are difficult to remove from smelted aluminum. Purified Al2O3 is obtained by processing natural bauxite.
The main starting material for aluminum production is aluminum oxide. It does not conduct electricity and has a very high melting point (about 2050oC), so it requires too much energy.
It is necessary to reduce the melting point of aluminum oxide to at least 1000oC. This method was simultaneously found by the Frenchman P. Heroux and the American C. Hall. They discovered that alumina dissolves well in molten cryolite, a mineral with the composition AlF3.3NaF. This melt is subjected to electrolysis at a temperature of only about 950oC in aluminum production. Reserves of cryolite in nature are insignificant, so synthetic cryolite was created, which significantly reduced the cost of aluminum production.
A molten mixture of Na3 [AlF6] cryolite and aluminum oxide is subjected to hydrolysis. A mixture containing about 10 weight percent Al2O3 melts at 960oC and has electrical conductivity, density and viscosity that are most favorable for the process. To further improve these characteristics, AlF3, CaF2 and MgF2 additives are added to the mixture. Thanks to this, electrolysis is possible at 950oC.
The electrolyser for aluminum smelting is an iron casing lined with refractory bricks on the inside. Its bottom (under), assembled from blocks of compressed coal, serves as a cathode. Anodes (one or more) are located on top: these are aluminum frames filled with coal briquettes. In modern plants, electrolysers are installed in series; each series consists of 150 or more electrolysers.
During electrolysis, aluminum is released at the cathode and oxygen at the anode. Aluminum, which has a higher density than the original melt, is collected at the bottom of the electrolyzer, from where it is periodically released. As the metal is released, new portions of aluminum oxide are added to the melt. The oxygen released during electrolysis interacts with the carbon of the anode, which burns out, forming CO and CO2.
The first aluminum smelter in Russia was built in 1932 in Volkhov.
Elastic limit
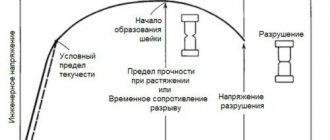
According to the definition, the modulus of elasticity shows how much stress must be applied to a solid body so that its deformation is 100%. However, all solids have an elastic limit, which is equal to 1% deformation. This means that if an appropriate force is applied and the body is deformed by an amount less than 1%, then after the cessation of this force the body exactly restores its original shape and size. If too much force is applied, at which the deformation value exceeds 1%, after the cessation of the external force, the body will no longer restore its original dimensions. In the latter case, they speak of the existence of residual deformation, which is evidence of exceeding the elastic limit of a given material.
Aluminum oxide Al2O3
Aluminum oxide Al2O3, also called alumina, occurs in nature in crystalline form, forming the mineral corundum. Corundum has very high hardness. Its transparent crystals, colored red or blue, represent the precious stones ruby and sapphire. Currently, rubies are produced artificially by alloying with alumina in an electric furnace. They are used not so much for decoration as for technical purposes, for example, for the manufacture of parts for precision instruments, watch stones, etc. Ruby crystals containing a small admixture of Cr2O3 are used as quantum generators - lasers that create a directed beam of monochromatic radiation.
Corundum and its fine-grained variety containing a large amount of impurities - emery, are used as abrasive materials.
Young's modulus in action
To determine the modulus of elasticity, as well as to understand how to use it, you can use a simple example with a spring. To do this, you need to take a metal spring and measure the area of the circle that its coils form. This is done using the simple formula S = πr², where n is pi equal to 3.14, and r is the radius of the spring coil.
Next, measure the length of the spring l0 without load. If you hang any load of mass m1 on a spring, then it will increase its length to a certain value l1. The elastic modulus E can be calculated based on knowledge of Hooke's law using the formula: E = m1gl0/(S(l1-l0)), where g is the acceleration of gravity. In this case, we note that the amount of spring deformation in the elastic region can greatly exceed 1%.
Knowing Young's modulus allows one to predict the magnitude of deformation under the action of a specific stress. In this case, if we hang another mass m2 on the spring, we obtain the following value of relative deformation: d = m2g/(SE), where d is the relative deformation in the elastic region.
System stiffness calculation
There are more complex problems in which it is necessary to calculate the total stiffness. In such applications, the springs are connected in series or in parallel.
Series connection of spring system
With a series connection, the overall rigidity of the system decreases. The formula for calculating the elasticity coefficient will be as follows:
1/k = 1/k1 + 1/k2 + … + 1/ki,
where k is the overall stiffness of the system, k1, k2, ..., ki are the individual stiffnesses of each element, i is the total number of all springs involved in the system.
Parallel connection of spring system
In the case when the springs are connected in parallel, the value of the overall elasticity coefficient of the system will increase. The formula for calculation will look like this:
k = k1 + k2 + … + ki.
Measurement of spring stiffness experimentally - in this video.
https://youtube.com/watch?v=YjfWehCZnf8
Isotropy and anisotropy
The modulus of elasticity is a characteristic of a material that describes the strength of the bonds between its atoms and molecules, but a given material can have several different Young's moduli.
The fact is that the properties of each solid depend on its internal structure. If the properties are the same in all spatial directions, then we are talking about an isotropic material. Such substances have a homogeneous structure, therefore the action of an external force in different directions on them causes the same reaction from the material. All amorphous materials are isotropic, such as rubber or glass.
Anisotropy is a phenomenon that is characterized by the dependence of the physical properties of a solid or liquid on direction. All metals and alloys based on them have one or another crystal lattice, that is, an ordered, rather than chaotic arrangement of ionic cores. For such materials, the elastic modulus varies depending on the axis of action of external stress. For example, metals with cubic symmetry, which include aluminum, copper, silver, refractory metals and others, have three different Young's moduli.
Types of loads
When using metals, different static and dynamic loads are applied. In the theory of strength, it is customary to define the following types of loads.
- Compression - an acting force compresses an object, causing a decrease in length along the direction of application of the load. This deformation is felt by frames, supporting surfaces, racks and a number of other structures that can withstand a certain weight. Bridges and crossings, car and tractor frames, foundations and reinforcement - all these structural elements are under constant compression.
Read also: Specific gravity of lead g cm3
- Tension - the load tends to lengthen the body in a certain direction. Lifting and transport machines and mechanisms experience similar loads when lifting and carrying loads.
- Shear and shear - such loading is observed in the case of forces directed along the same axis towards each other. Connecting elements (bolts, screws, rivets and other hardware) experience this type of load. The design of housings, metal frames, gearboxes and other components of mechanisms and machines necessarily contains connecting parts. The performance of devices depends on their strength.
- Torsion - if a pair of forces acting on an object are located at a certain distance from each other, then a torque occurs. These forces tend to produce torsional deformation. Similar loads are observed in gearboxes; the shafts experience just such a load. It is most often inconsistent in meaning. Over time, the magnitude of the acting forces changes.
- Bending – a load that changes the curvature of objects is considered bending. Bridges, crossbars, consoles, lifting and transport mechanisms and other parts experience similar loading.
Shear modulus
A description of the elastic properties of even an isotropic material does not require knowledge of Young’s modulus alone. Because, in addition to tension and compression, the material can be affected by shear stresses or torsional stresses. In this case, he will react to external force differently. To describe elastic shear deformation, an analogue of Young's modulus, the shear modulus or elastic modulus of the second kind, is introduced.
All materials are less resistant to shear stress than to tension or compression, so the value of the shear modulus for them is 2-3 times less than the value of Young’s modulus. Thus, for titanium, whose Young’s modulus is 107 GPa, the shear modulus is only 40 GPa; for steel, these figures are 210 GPa and 80 GPa, respectively.
Work of deformation
The greater the internal forces of interaction between the particles of the material, the higher the strength of the material. Therefore, the value of elongation resistance per unit volume of a material can serve as a characteristic of its strength. In this case, the tensile strength is not an exhaustive characteristic of the strength properties of a given material, since it characterizes only the cross sections. When a rupture occurs, the interconnections are destroyed over the entire cross-sectional area, and during shears, which occur during any plastic deformation, only local interconnections are destroyed. To destroy these connections, a certain amount of work of internal interaction forces is expended, which is equal to the work of external forces expended on displacement:
A = РΔl/2 (318.4.1)
where 1/2 is the result of the static action of the load, increasing from 0 to P at the time of its application (average value (0 + P)/2)
During elastic deformation, the work of forces is determined by the area of the triangle OAB (see Fig. 318.1). Total work expended on the deformation of the sample and its destruction:
A = ηРmaxΔlmax (318.4.2)
where η is the coefficient of completeness of the diagram, equal to the ratio of the area of the entire diagram, limited by the curve AM and straight lines OA, MN and ON, to the area of a rectangle with sides 0Рmax (along the P axis) and Δlmax (dotted line in Fig. 318.1). In this case, it is necessary to subtract the work determined by the area of the triangle MNL (related to elastic deformations).
The work spent on plastic deformation and destruction of the sample is one of the important characteristics of the material that determines the degree of its fragility.
Modulus of elasticity of wood
Wood is an anisotropic material because wood fibers are oriented along a specific direction. It is along the fibers that the elastic modulus of wood is measured, since across the fibers it is 1-2 orders of magnitude smaller. Knowledge of Young's modulus for wood plays an important role and is taken into account when designing structures made of wood panels.
The values of the modulus of elasticity of wood for some types of trees are given in the table below.
| Type of tree | Young's modulus in GPa |
| bay tree | 14 |
| Eucalyptus | 18 |
| Cedar | 8 |
| Spruce | 11 |
| Pine | 10 |
| Oak | 12 |
It should be noted that the given values may differ by about 1 GPa for a particular tree, since its Young's modulus is affected by wood density and growing conditions.
The shear moduli for various tree species are within 1-2 GPa, for example, for pine it is 1.21 GPa, and for oak it is 1.38 GPa, that is, wood practically does not resist shear stresses. This fact must be taken into account in the manufacture of wooden load-bearing structures, which are designed so that they work only in tension or compression.
Poisson's ratio
When a load is applied to the rod, in addition to the longitudinal deformation ε, a transverse deformation ε1 appears. The transverse strain ratio, or Poisson's ratio μ, is the ratio of ε1 to ε.
The Poisson's ratio of wood is determined by compressing rectangular prismatic samples with a cross-section of 40x40 mm and a height of 150 mm. To measure the deformation, six strain gauges with a base of 20 mm and a gear ratio of about 1000 are installed on the sample. Of these strain gauges, two record longitudinal strain (deformation in the direction of the compression force), the other four measure transverse strains in two mutually perpendicular directions. Each of the samples is loaded six times up to 400 and 1600 kg when compressed along the fibers, up to 40 and 160 kg when compressed across the fibers.
For pine and spruce wood, Poisson's ratio with a force directed along the fibers v0=0.5.
Elasticity characteristics of metals
When compared with the Young's modulus of wood, the average values of this value for metals and alloys are an order of magnitude greater, as shown in the following table.
| Metal | Young's modulus in GPa |
| Bronze | 120 |
| Copper | 110 |
| Steel | 210 |
| Titanium | 107 |
| Nickel | 204 |
The elastic properties of metals that have a cubic system are described by three elastic constants. These metals include copper, nickel, aluminum, and iron. If a metal has a hexagonal system, then six constants are already needed to describe its elastic characteristics.
For metallic systems, Young's modulus is measured within 0.2% strain, since larger values can already occur in the inelastic region.