Each measurement is a comparison of the measured quantity with another homogeneous quantity, which is considered unitary. Theoretically, the units for all quantities in physics can be chosen to be independent of each other. But this is extremely inconvenient, since for each value one should enter its own standard. In addition, in all physical equations that reflect the relationship between different quantities, numerical coefficients would arise.
The main feature of the currently used systems of units is that there are certain relationships between units of different quantities. These relationships are established by the physical laws (definitions) that relate the measured quantities to each other. Thus, the unit of speed is chosen in such a way that it is expressed in terms of units of distance and time. When selecting speed units, the speed definition is used. The unit of force, for example, is established using Newton's second law.
When constructing a specific system of units, several physical quantities are selected, the units of which are set independently of each other. Units of such quantities are called basic. The units of other quantities are expressed in terms of the basic ones, they are called derivatives.
Table of units of measurement "Acoustics"
| Physical quantity | Symbol | Unit of measurement of physical quantity | Unit change physical led | Description | Notes |
| Sound pressure | p | pascal | Pa | Variable excess pressure arising in an elastic medium when a sound wave passes through it | |
| Volume velocity | c, V | cubic meter per second | m3/s | The ratio of the volume of raw materials supplied to the reactor per hour to the volume of catalyst | |
| Sound speed | v, u | meter per second | m/s | Velocity of propagation of elastic waves in a medium | |
| Sound intensity | l | watt per square meter | W/m2 | A quantity characterizing the power transferred by a sound wave in the direction of propagation | scalar physical quantity |
| Acoustic impedance | Za, Ra | pascal second per cubic meter | Pa•s/m3 | The ratio of the amplitude of sound pressure in a medium to the vibrational speed of its particles when a sound wave passes through the medium | |
| Mechanical resistance | Rm | newton second per meter | N•s/m | Indicates the force required to move a body at each frequency |
Designation: height, width, length. Width
Constructing drawings is not an easy task, but you can’t do without it in the modern world. After all, in order to make even the most ordinary item (a tiny bolt or nut, a shelf for books, the design of a new dress, etc.), you first need to carry out the appropriate calculations and draw a drawing of the future product. However, often one person draws it up, and another person produces something according to this scheme.
To avoid confusion in understanding the depicted object and its parameters, conventions for length, width, height and other quantities used in design are accepted all over the world. What are they? Let's find out.
Quantities
Area, length, width, height and other designations of a similar nature are not only physical, but also mathematical quantities.
Their single letter designation (used by all countries) was established in the mid-twentieth century by the International System of Units (SI) and is still used to this day. It is for this reason that all such parameters are indicated in Latin, and not in Cyrillic letters or Arabic script. In order not to create certain difficulties, when developing design documentation standards in most modern countries, it was decided to use almost the same conventions that are used in physics or geometry.
Any school graduate remembers that depending on whether a two-dimensional or three-dimensional figure (product) is depicted in the drawing, it has a set of basic parameters. If there are two dimensions, these are width and length, if there are three, height is also added.
So, first, let's find out how to correctly indicate length, width, height in the drawings.
Width
As mentioned above, in mathematics the quantity in question is one of the three spatial dimensions of any object, provided that its measurements are made in the transverse direction. So what is width famous for? It is designated by the letter “B”. This is known all over the world. Moreover, according to GOST, it is permissible to use both capital and lowercase Latin letters. The question often arises as to why this particular letter was chosen. After all, the abbreviation is usually made according to the first letter of the Latin, Greek or English name of the quantity. In this case, the width in English will look like “width”.
Probably the point here is that this parameter was initially most widely used in geometry. In this science, when describing figures, length, width, height are often denoted by the letters “a”, “b”, “c”. According to this tradition, when choosing, the letter "B" (or "b") was borrowed from the SI system (although symbols other than geometric ones began to be used for the other two dimensions).
Most believe that this was done so as not to confuse width (designated with the letter "B"/"b") with weight. The fact is that the latter is sometimes referred to as “W” (short for the English name weight), although the use of other letters (“G” and “P”) is also acceptable. According to international standards of the SI system, width is measured in meters or multiples (multiples) of their units. It is worth noting that in geometry it is sometimes also acceptable to use “w” to denote width, but in physics and other exact sciences such a designation is usually not used.
Length
As already mentioned, in mathematics, length, height, width are three spatial dimensions. Moreover, if width is a linear dimension in the transverse direction, then length is in the longitudinal direction. Considering it as a quantity of physics, one can understand that this word means a numerical characteristic of the length of lines.
In English this term is called length. It is because of this that this value is denoted by the capital or lowercase initial letter of the word - “L”. Like width, length is measured in meters or their multiples (multiples).
Height
The presence of this value indicates that we have to deal with a more complex - three-dimensional space. Unlike length and width, height numerically characterizes the size of an object in the vertical direction.
In English it is written as "height". Therefore, according to international standards, it is denoted by the Latin letter “H” / “h”. In addition to height, in drawings sometimes this letter also acts as a designation for depth. Height, width and length - all these parameters are measured in meters and their multiples and submultiples (kilometers, centimeters, millimeters, etc.).
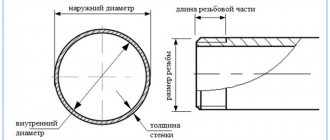
Radius and diameter
In addition to the parameters discussed, when drawing up drawings you have to deal with others.
For example, when working with circles, it becomes necessary to determine their radius. This is the name of the segment that connects two points. The first of them is the center. The second is located directly on the circle itself. In Latin this word looks like "radius". Hence the generally accepted abbreviation: lowercase or capital “R”/“r”.
When drawing circles, in addition to the radius, you often have to deal with a phenomenon close to it - diameter. It is also a line segment connecting two points on a circle. In this case, it necessarily passes through the center.
Numerically, the diameter is equal to two radii. In English this word is written like this: “diameter”. Hence the abbreviation - large or small Latin letter “D” / “d”. Often the diameter in the drawings is indicated using a crossed out circle - “Ø”.
Although this is a common abbreviation, it is worth keeping in mind that GOST provides for the use of only the Latin “D” / “d”.
Thickness
Most of us remember school mathematics lessons. Even then, teachers told us that it is customary to use the Latin letter “s” to denote a quantity such as area. However, according to generally accepted standards, a completely different parameter is written in drawings in this way - thickness.
Why is that? It is known that in the case of height, width, length, the designation by letters could be explained by their writing or tradition. It’s just that thickness in English looks like “thickness”, and in Latin it looks like “crassities”. It is also not clear why, unlike other quantities, thickness can only be indicated in lowercase letters. The notation "s" is also used to describe the thickness of pages, walls, ribs, etc.
Perimeter and area
Unlike all the quantities listed above, the word “perimeter” does not come from Latin or English, but from Greek. It is derived from “περιμετρέο” (“to measure the circumference”). And today this term has retained its meaning (the total length of the boundaries of the figure). Subsequently, the word entered the English language (“perimeter”) and was fixed in the SI system in the form of an abbreviation with the letter “P”.
Area is a quantity that shows the quantitative characteristics of a geometric figure that has two dimensions (length and width). Unlike everything listed earlier, it is measured in square meters (as well as in submultiples and multiples thereof). As for the letter designation of the area, it differs in different areas. For example, in mathematics this is the Latin letter “S”, familiar to everyone since childhood. Why this is so - no information.
Some people unknowingly think that this is due to the English spelling of the word "square". However, in it the mathematical area is “area”, and “square” is the area in the architectural sense. By the way, it is worth remembering that “square” is the name of the geometric figure “square”. So you should be careful when studying drawings in English. Due to the translation of “area” in some disciplines, the letter “A” is used as a designation. In rare cases, “F” is also used, but in physics this letter means a quantity called “force” (“fortis”).
Other common abbreviations
The designations for height, width, length, thickness, radius, and diameter are the most commonly used when drawing up drawings. However, there are other quantities that are also often present in them. For example, lowercase "t". In physics, this means “temperature”, however, according to GOST of the Unified System of Design Documentation, this letter is the pitch (of helical springs, rivet joints, etc.). However, it is not used when it comes to gears and threads.
The capital and lowercase letter “A”/“a” (according to the same standards) in the drawings is used to denote not the area, but the center-to-center and center-to-center distance. In addition to different sizes, in drawings it is often necessary to indicate angles of different sizes. For this purpose, it is customary to use lowercase letters of the Greek alphabet. The most commonly used ones are “α”, “β”, “γ” and “δ”. However, it is acceptable to use others.
What standard defines the letter designation of length, width, height, area and other quantities?
As mentioned above, so that there is no misunderstanding when reading the drawing, representatives of different nations have adopted common standards for letter designation. In other words, if you are in doubt about the interpretation of a particular abbreviation, look at GOSTs. This way you will learn how to correctly indicate height, width, length, diameter, radius, and so on.
For the Russian Federation, such a regulatory document is GOST 2.321-84. It was introduced back in March 1984 (during the times of the USSR), to replace the outdated GOST 3452-59.
fb.ru
Table of units of measurement “Periodic phenomena, oscillations and waves”
| Physical quantity | Symbol | Unit of measurement of physical quantity | Unit change physical led | Description | Notes |
| Period | T | second | With | The period of time during which the system makes one complete oscillation | |
| Batch frequency | v, f | hertz | Hz = (s−1) | The number of repetitions of an event per unit of time. | |
| Cyclic (circular) frequency | ω | radians per second | rad/s | Cyclic frequency of electromagnetic oscillations in an oscillatory circuit. | |
| Rotation frequency | n | second to the minus first power | s-1 | A periodic process equal to the number of complete cycles completed per unit of time. | |
| Wavelength | λ | meter | m | The distance between two points in space closest to each other at which the oscillations occur in the same phase. | |
| Wave number | k | meter to the minus first power | m-1 | Spatial wave frequency |
Table of units of measurement "Mechanics"
| Physical quantity | Symbol | Unit of measurement of physical quantity | Unit change physical led | Description | Notes |
| Weight | m | kilogram | kg | A quantity that determines the inertial and gravitational properties of bodies. | extensive quantity |
| Density | ρ | kilogram per cubic meter | kg/m3 | Mass per unit volume. | intensive quantity |
| Surface density | ρA | Mass per unit area. | kg/m2 | Ratio of body mass to surface area | |
| Linear density | ρl | Mass per unit length. | kg/m | Ratio of body mass to its linear parameter | |
| Specific volume | v | cubic meter per kilogram | m3/kg | Volume occupied by a unit mass of a substance | |
| Mass flow | Qm | kilogram per second | kg/s | The mass of a substance that passes through a given cross-sectional area of a flow per unit time | |
| Volume flow | Qv | cubic meter per second | m3/s | Volume flow of liquid or gas | |
| Pulse | P | kilogram-meter per second | kg•m/s | Product of mass and speed of a body. | extensive, conserved quantity |
| Momentum | L | kilogram-meter squared per second | kg•m2/s | A measure of the rotation of an object. | conserved quantity |
| Moment of inertia | J | kilogram meter squared | kg•m2 | A measure of the inertia of an object during rotation. | tensor quantity |
| Strength, weight | F, Q | newton | N | An external cause of acceleration acting on an object. | vector |
| Moment of power | M | newton meter | N•m = (kg m2/s2) | The product of a force and the length of a perpendicular drawn from a point to the line of action of the force. | vector |
| Impulse force | I | newton second | N•s | Product of force and the duration of its action | vector |
| Pressure, mechanical stress | p , σ | pascal | Pa = ( kg/(m s2)) | Force per unit area. | intensive quantity |
| Job | A | joule | J = (kg m2/s2) | Dot product of force and displacement. | scalar |
| Energy | E, U | joule | J = (kg m2/s2) | The ability of a body or system to do work. | extensive, conserved quantity, scalar |
| Power | N | watt | W = (kg m2/s3) | Rate of change of energy. |
Table of units of measurement "Molecular physics"
| Physical quantity | Symbol | Unit of measurement of physical quantity | Unit change physical led | Description | Notes |
| Quantity of substance | v, n | mole | mole | The number of similar structural units that make up a substance. | Extensive value |
| Molar mass | M , μ | kilogram per mole | kg/mol | The ratio of the mass of a substance to the number of moles of that substance. | |
| Molar energy | Hmol | joule per mole | J/mol | Energy of a thermodynamic system. | |
| Molar heat capacity | resins | joule per mole kelvin | J/(mol•K) | The heat capacity of one mole of a substance. | |
| Molecular concentration | c, n | meter to the minus third power | m-3 | The number of molecules contained in a unit volume. | |
| Mass concentration | ρ | kilogram per cubic meter | kg/m3 | The ratio of the mass of a component contained in a mixture to the volume of the mixture. | |
| Molar concentration | resins | mole per cubic meter | mol/m3 | The content of the component relative to the entire mixture. | |
| Ion mobility | V , μ | square meter per volt second | m2/(V•s) | The proportionality coefficient between the drift velocity of carriers and the applied external electric field. |
Table of units of measurement “Optics, electromagnetic radiation”
| Physical quantity | Symbol | Unit of measurement of physical quantity | Unit change physical led | Description | Notes |
| The power of light | J, I | candela | cd | The amount of light energy emitted in a given direction per unit time. | Luminous, extensive value |
| Light flow | F | lumen | lm | Physical quantity characterizing the amount of “light” power in the corresponding radiation flux | |
| Light energy | Q | lumen-second | lm•s | Physical quantity characterizes the ability of energy transferred by light to cause visual sensations in a person | |
| Illumination | E | luxury | OK | The ratio of the luminous flux incident on a small area of a surface to its area. | |
| Luminosity | M | lumen per square meter | lm/m2 | Luminous quantity representing luminous flux | |
| Brightness | L,B | candela per square meter | cd/m2 | Luminous intensity emitted per unit surface area in a specific direction | |
| Radiation energy | E,W | joule | J = (kg m2/s2) | Energy transferred by optical radiation |
Table of units of measurement “Space and time”
| Physical quantity | Symbol | Unit of measurement of physical quantity | Unit change physical led | Description | Notes |
| Length | l, s, d | meter | m | The extent of an object in one dimension. | |
| Square | S | square meter | m2 | The extent of an object in two dimensions. | |
| Volume, capacity | V | cubic meter | m3 | The extent of an object in three dimensions. | extensive quantity |
| Time | t | second | With | Duration of the event. | |
| Flat angle | α , φ | radian | glad | The amount of change in direction. | |
| Solid angle | α , β , γ | steradian | Wed | Part of space | |
| Linear speed | v | meter per second | m/s | The speed of changing body coordinates. | vector |
| Linear acceleration | a,w | meters per second squared | m/s2 | The rate of change in the speed of an object. | vector |
| Angular velocity | ω | radians per second | rad/s = (s−1) | Angle change rate. | |
| Angular acceleration | ε | radian per second squared | rad/s2 = (s−2) | Rate of change of angular velocity |
Table of units of measurement “Atomic and nuclear physics. Radioactivity"
| Physical quantity | Symbol | Unit of measurement of physical quantity | Unit change physical led | Description | Notes |
| Mass (rest mass) | m | kilogram | kg | The mass of an object at rest. | |
| Mass defect | Δ | kilogram | kg | A quantity expressing the influence of internal interactions on the mass of a composite particle | |
| Elementary electric charge | e | pendant | Cl | The minimum portion (quantum) of electric charge observed in nature in free long-lived particles | |
| Communication energy | Est | joule | J = (kg m2/s2) | The difference between the energy of a state in which the constituent parts of the system are infinitely distant | |
| Half-life, average lifetime | T, τ | second | With | The time during which the system decays in the approximate ratio of 1/2 | |
| Effective cross section | σ | square meter | m2 | A quantity characterizing the probability of interaction of an elementary particle with an atomic nucleus or another particle | |
| Nuclide activity | A | becquerel | Bk | A value equal to the ratio of the total number of decays of radioactive nuclide nuclei in the source to the decay time | |
| Energy of ionizing radiation | E,W | joule | J = (kg m2/s2) | Type of energy released by atoms in the form of electromagnetic waves (gamma or x-rays) or particles | |
| Absorbed dose of ionizing radiation | D | gray | Gr | The dose at which 1 joule of ionizing radiation energy is transferred to a mass of 1 kg | |
| Equivalent dose of ionizing radiation | H , Deck | sievert | Sv | Absorbed dose of any ionizing radiation equal to 100 erg per 1 gram of irradiated substance | |
| Exposure dose of X-ray and gamma radiation | X | pendant per kilogram | C/kg | ratio of the total electric charge of ions of the same sign from external gamma radiation |
Table of units of measurement “Thermal phenomena”
| Physical quantity | Symbol | Unit of measurement of physical quantity | Unit change physical led | Description | Notes |
| Temperature | T | kelvin | TO | The average kinetic energy of the object's particles. | Intensive value |
| Temperature coefficient | α | kelvin to the minus first power | K-1 | Dependence of electrical resistance on temperature | |
| Temperature gradient | gradT | kelvin per meter | K/m | Change in temperature per unit length in the direction of heat propagation. | |
| Heat (amount of heat) | Q | joule | J = (kg m2/s2) | Energy transferred from one body to another by non-mechanical means | |
| Specific heat | q | joule per kilogram | J/kg | The amount of heat that must be supplied to a substance taken at its melting point in order to melt it. | |
| Heat capacity | C | joule per kelvin | J/C | The amount of heat absorbed (released) by a body during the heating process. | |
| Specific heat | c | joule per kilogram kelvin | J/(kg•K) | Heat capacity of a unit mass of a substance. | |
| Entropy | S | joule per kilogram | J/kg | A measure of the irreversible dissipation of energy or the uselessness of energy. |
Indication of depth in the drawing - how width is indicated in construction
Quantities |
| Weight |
| Time |
| Height |
| Pressure |
| Diameter |
| Length |
| Path length |
| Impulse (amount of movement) |
| Quantity of substance |
| Stiffness coefficient (stiffness) |
| Safety factor |
| Efficiency |
| Rolling friction coefficient |
| Sliding friction coefficient |
| Weight |
| Atomic mass |
| Electron mass |
| Mechanical stress |
| Modulus of elasticity (Young's modulus) |
| Moment of power |
| Power |
| Volume, capacity |
| Oscillation period |
| Density |
| Square |
| Surface tension |
| Constant gravitational |
| Tensile strength |
| Job |
| Radius |
| Force, gravity |
| Linear speed |
| Angular speed |
| Thickness |
| Acceleration linear |
| Acceleration of gravity |
| Frequency |
| Rotation frequency |
| Width |
| Energy |
| Kinetic energy |
| Potential energy |
| Wavelength |
| Sound power |
| Sound energy |
| Sound intensity |
| Sound speed |
| Frequency |
Thermal and molecular physics quantities |
| Absolute humidity |
| Gas constant (molar) |
| Quantity of heat |
| Efficiency |
| Relative humidity |
| Relative molecular weight |
| Avogadro's constant (number) |
| Boltzmann's constant |
| Loschmidt's constant (number) |
| Curie temperature |
| Temperature on the Celsius scale |
| Thermodynamic temperature (absolute temperature) |
| Temperature coefficient of linear expansion |
| Temperature coefficient of volumetric expansion |
| Specific heat |
| Specific heat of vaporization |
| Specific heat of fusion |
| Specific heat of combustion of fuel (abbreviated as heat of combustion of fuel) |
| Number of molecules |
| Energy internal |
Electrical and magnetic quantities |
| Dielectric constant of vacuum (electric constant) |
| Inductance |
| Self-induction coefficient |
| Transformation ratio |
| Magnetic induction |
| Magnetic permeability of vacuum (magnetic constant) |
| Magnetic flux |
| Electric circuit power |
| Magnetic field strength |
| Electric field strength |
| Volume density of electric charge |
| Relative dielectric constant |
| Relative magnetic permeability |
| Specific magnetic field energy density |
| Specific electric field energy density |
| Surface charge density |
| Electric current density |
| Faraday's constant (number) |
| Dielectric constant |
| Electron work function |
| Potential difference |
| Current strength |
| Temperature coefficient of electrical resistance |
| Electrical conductivity |
| Electrical resistivity |
| Electric current frequency |
| Number of winding turns |
| Electrical capacity |
| Electrical induction |
| Electrical conductivity |
| Electric dipole moment of a molecule |
| Electric charge (amount of electricity) |
| Electric potential |
| Electrical voltage |
| Electrical resistance |
| Electromotive force |
| Electrochemical equivalent |
| Magnetic field energy |
| Electric field energy |
| Energy Electromagnetic |
| Wavelength |
| Illumination |
| Oscillation period |
| Radiation flux density |
| Index of refraction |
| Light flow |
| Light power lens |
| The power of light |
| Speed of light |
| Magnification linear |
| Magnification of eyepiece, microscope, magnifying glass |
| Beam reflection angle |
| Beam angle |
| Focal length |
| Oscillation frequency |
| Radiation energy |
| Light energy |
| Atomic mass relative |
| Half-life |
| Mass defect |
| Electron charge |
| Atomic mass |
| Neutron mass |
| Proton mass |
| Electron mass |
| Planck's constant |
| Electron radius |