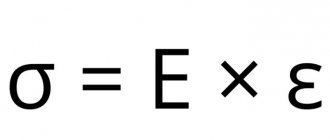Ratio of shear stress to shear strain
| Shear modulus | |
| Common symbols | G, S |
| SI unit | pascal |
| Derivatives from other quantities | G = / G = / 2 (1+ ) |
Shear strain
In materials science, shear modulus
or
modulus of stiffness
, denoted
G
, or sometimes
S
or
M
, is a measure of the elastic shear stiffness of a material and is defined as the ratio of shear stress to shear strain: [1]
g = d e f τ x y γ x y = F / A Δ X / l = F l A Δ X {\displaystyle G\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\tau _{xy}}{\gamma _{xy}}} ={\frac {F/A}{\Delta x/l}}={\frac {Fl}{A\Delta x}}}
where
τ xy = F / A {\displaystyle \tau _{xy}=F/A\,} = shear stress F {\displaystyle F} is the force that acts A {\displaystyle A} is the area that the force γ acts on xy {\displaystyle \gamma _{xy}} = shear strain. In mechanical engineering, in other := Δ x / l = tan θ {\displaystyle :=\Delta x/l=\tan \theta } := θ {\displaystyle :=\theta } Δ x {\displaystyle \Delta x } lateral displacement l {\displaystyle l} initial length
The derived unit of shear modulus in the system is the pascal (Pa), although it is usually expressed in gigapascals (GPa) or thousand pounds per square inch (ksi). Its dimensional form is M 1 l -1 T -2, replacing the forces
for
mass
acceleration
times .
Explanation[edit]
| Material | Typical values for shear modulus (GPa) (at room temperature) |
| Diamond [2] | 478,0 |
| Steel [3] | 79,3 |
| Iron [4] | 52,5 |
| Copper [5] | 44,7 |
| Titan [3] | 41,4 |
| Glass [3] | 26,2 |
| Aluminum [3] | 25,5 |
| Polyethylene [3] | 0,117 |
| Rubber [6] | 0,0006 |
| Granite [7] [8] | 24 |
| Slate [7] [8] | 1.6 |
| Limestone [7] [8] | 24 |
| Chalk [7] [8] | 3,2 |
| Sandstone [7] [8] | 0,4 |
| Tree | 4 |
Shear modulus is one of several quantities for measuring the stiffness of materials. They all arise in the generalized Hooke's law:
- Young's modulus E
describes the deformation response of a material to a uniaxial stress in the direction of that stress (for example, pulling on the ends of a wire or placing a weight on the top of a column, causing the wire to become longer and the column to lose height). - the Poisson's ratio ν
describes the response in directions orthogonal to this uniaxial stress (the wire becomes thinner and the column thicker), - the bulk modulus of elasticity K
describes the response of a material to (uniform) hydrostatic pressure (e.g. pressure at the bottom of an ocean or deep pool), - The shear modulus G
describes the response of a material to shear stress (like cutting it with blunt scissors). These modules are not independent, and for isotropic materials they are related by the equations. [9] 2 G ( 1 + ν ) = E = 3 K ( 1 − 2 ν ) {\displaystyle 2G(1+\nu )=E=3K(1-2\nu )}
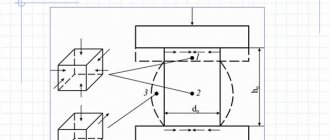
Shear modulus relates to the deformation of a solid when it experiences a force parallel to one of its surfaces while its opposite side experiences an opposing force (such as friction). If an object is shaped like a rectangular prism, it deforms into a parallelepiped. Anisotropic materials such as wood, paper, and virtually all single crystals exhibit different material responses to stress or strain when tested in different directions. In this case, it may be necessary to use the full tensor expression of the elastic constants rather than a single scalar value.
One possible definition of a fluid is a material with zero shear modulus.
Shear modulus equation
The shear modulus is determined by measuring the deformation of a solid body from the application of a force parallel to one surface of the solid body, while an opposing force acts on its opposite surface and holds the solid body in place. Think of shear as pushing one side of a block with friction as the opposing force. Another example is trying to cut wire or hair with dull scissors.
Equation for shear modulus:
G = τ xy /γ xy = F/A/Δx/l = Fl/AΔx
Where:
- G - shear modulus or stiffness modulus
- τ xy—shear stress
- γ xy—shear strain
- A is the area affected by the force
- Δx - lateral displacement
- l - initial length
The shear strain is Δx/l = tan θ or sometimes = θ, where θ is the angle formed by the strain caused by the applied force.
Strain – dimensionless number
The use of the concept of “deformation” makes it possible to quantitatively describe changes in the size and shape of a body that occur when stresses are applied, which, in turn, arise when a certain load is applied. It is important to note that strain is a “pure”, dimensionless number. Strain does not have any units of measurement. To calculate the deformation, you need to compare the initial, original dimensions or shape of a body before applying a load with the same dimensions or shape of the same body under load.
The formula used to calculate deformation has values of the same dimension (meters, centimeters, millimeters) in both the denominator and numerator. Therefore, it is clear from school physics that these dimensional units cancel each other, and as a result we get a dimensionless number. This procedure is clearly visible when calculating stresses and strains for a simple tensile test.
General concepts
The modulus of elasticity (Young's modulus) is an indicator of the mechanical property of a material, characterizing its resistance to tensile deformation . In other words, this is the value of the ductility of the material. The higher the elastic modulus values, the less any rod will stretch under other equal loads (sectional area, load magnitude, etc.).
Young's modulus in the theory of elasticity is denoted by the letter E. It is a component of Hooke's law (on the deformation of elastic bodies). This value relates the stress arising in the sample and its deformation.
This value is measured according to the standard international system of units in MPa (Megapascals) . But in practice, engineers are more inclined to use the kgf/cm2 dimension.
This indicator is determined empirically in scientific laboratories. The essence of this method is the tearing of dumbbell-shaped samples of material using special equipment. Having found out the elongation and tension at which the sample failed, divide the variable data into each other. The resulting value is the (Young's) modulus of elasticity.
In this way, only the Young’s modulus of elastic materials is determined: copper, steel, etc. And brittle materials are compressed until cracks appear: concrete, cast iron and the like.
Tension diagram
The engineering stress σ, which is used in the stress-strain diagram in Figure 2, is the average or nominal stress in the fracture specimen. It is obtained by dividing the load value F by the initial - unloaded - cross-sectional area A0 of this sample.
σ = F/A0.
Figure 2 – Engineering stress-strain diagram. It is more often called a stretch diagram. The intersection of the dotted line with the stress-strain diagram gives the value of the yield strength at permanent deformation, usually 0.2%.
As the stress in the tensile specimen increases, the distance between the reference length marks changes under the influence of the applied stresses. The resulting strain ɛ, which is indicated on the engineering stress-strain diagram, is the average or nominal linear - uniaxial - strain. The magnitude of this deformation is obtained by dividing the change in the base length of the sample δ by the original base length of the sample L0:
ɛ = δ/L0 = ΔL/L0 = (L - L0)/L0
Since both the engineering stress (σ) and strain (ɛ) are obtained by dividing the load on the specimen and elongating the specimen by the same constant amount L0, the shape of the load-elongation and stress-strain diagrams are the same.
The shape and dimensions of the steel tensile diagram depend on:
- chemical composition of steel,
- form of heat treatment,
- modes of plastic deformation,
- loading speed,
- temperature and
- stress state during a tensile test.
The mechanical properties of steel are most often determined by the tensile test described above. Steel characteristics that are commonly used to describe the stress-strain curve of a particular steel include:
- tensile strength (temporary tensile strength),
- yield strength,
- elongation of the base length of the sample (in percent),
- narrowing of the cross-sectional area of the sample (in percent).
Various types of tests, which involve applying different loads to a steel specimen, are also used to determine other mechanical properties of steel. Examples of such mechanical properties of steel are modulus of elasticity, hardness, fatigue resistance and toughness.
Effect of temperature and pressure
As you would expect, the response of a material to an applied force varies with temperature and pressure. In metals, the shear modulus generally decreases with increasing temperature. Hardness decreases with increasing pressure. Three models are used to predict the effect of temperature and pressure on the shear modulus: the mechanical threshold stress (MTS) plastic flow model, the Nadal and Lepoak shear modulus (NP) model, and the Steinberg-Cochran-Guinan (SCG) shear modulus. model. For metals, there is usually a region of temperature and pressure in which the change in shear modulus is linear. Beyond this range, the modeling behavior is more complex.
Isotropic and anisotropic materials
Some materials are shear isotropic, meaning that the deformation in response to force is the same regardless of orientation. Other materials are anisotropic and respond differently to stress or strain depending on orientation. Anisotropic materials are much more susceptible to shear along one axis than the other. For example, consider the behavior of a block of wood and how it might respond to a force applied parallel to the grain of the wood compared to its response to a force applied perpendicular to the grain. Let's consider how a diamond reacts to an applied force. The rate of crystal shear depends on the orientation of the force relative to the crystal lattice.
All mechanical properties of steel
An almost complete list of mechanical properties for steel includes:
- Hardness. Indentation resistance measure
- Linear elasticity coefficients for tensile, compressive and shear loads
- Yield strength (under tensile, compressive and shear loads). Shows the stress level at which irreversible plastic deformation occurs
- Tensile strength (under tensile, compressive and shear loads). Shows the maximum engineering stresses that a material can withstand without failure. Ultimate tensile strength - temporary resistance to rupture - is usually associated with the onset of necking on a tensile specimen (see Figure 2)
- Fatigue strength. Shows the level of cyclic stresses that cause failure due to metal fatigue after a certain number of loading cycles, for example, 1 million
- Impact strength. Shows the level of shock energy absorption from loads that the metal is capable of absorbing before failure
- Fracture toughness. Shows the level of fracture resistance when the product contains defects and stress concentrators
- Resistance to high temperature creep and fracture.
- Wear resistance.
How to determine the modulus of elasticity of steel
There are several ways to determine elastic moduli for different grades of steel:
- according to reference data from tables;
- experimental methods for a small sample;
- calculation methods, knowing the necessary data.
The hardness of steel depends on its chemical composition and the type of crystal lattice, on the density achieved as a result of processing. The strength of its structures is determined by such important factors as product parameters, including dimensions, operating loads, and their duration. When calculations are performed according to standardized methods, the result is deliberately overestimated in order to prevent possible accidents and breakdowns.
However, the resistance of steel to deformation is determined initially by its grade, that is, by the presence of impurities in the alloy.
The table shows the elastic modulus of steel of the most popular grades, and its shear modulus is 80-81 GPa.
| Steel | Module (E), GPa |
| carbon | 195-205 |
| alloyed | 206-235 |
| Art.3, Art.5 | 210 |
| steel 45 | 200 |
| 25G2S, 30HG2S | 200 |
The table shows that the lowest strength values for steel are 45, 25G2S, 30KhG2S, and stainless steel has the highest - 235 GPa.
The experimental method of determination is to determine the relative elongation of a small steel sample on an installation, followed by calculation.
The method is based on the conclusion that stretching a steel sample to the elastic limit obeys Hooke’s law (1). Knowing the applied force (F) and the area of the part (A), having found out its elongation (Δl), you can calculate E:
Calculations are carried out in mm and MPa.
To design structures, it is always necessary to know or calculate at least two different elastic moduli. Based on the stiffness coefficient, you can move on to other types of resistance to external influences for steel: bending elasticity and volumetric elasticity.