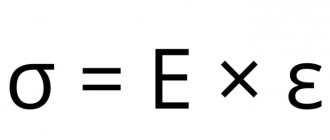Отношение напряжения сдвига к деформации сдвига
| Модуль сдвига | |
| Общие символы | G , S |
| Единица СИ | паскаль |
| Производные от других величин | G = / G = / 2 (1+ ) |
Деформация сдвига
В науке материалов , модуль сдвига
или
модулем жесткости
, обозначаемой
G
, или иногда
S
или
М
, является мерой упругого сдвига жесткости материала и определяется как отношение напряжения сдвига к сдвиговой деформации : [1]
грамм знак равно d е ж τ Икс y γ Икс y знак равно F / А Δ Икс / л знак равно F л А Δ Икс {\displaystyle G\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\tau _{xy}}{\gamma _{xy}}}={\frac {F/A}{\Delta x/l}}={\frac {Fl}{A\Delta x}}}
куда
τ x y = F / A {\displaystyle \tau _{xy}=F/A\,} = напряжение сдвига F {\displaystyle F} это сила, которая действует A {\displaystyle A} это область, на которую действует сила γ x y {\displaystyle \gamma _{xy}} = деформация сдвига. В машиностроении , в другом := Δ x / l = tan θ {\displaystyle :=\Delta x/l=\tan \theta } := θ {\displaystyle :=\theta } Δ x {\displaystyle \Delta x} поперечное смещение l {\displaystyle l} начальная длина
Производной единицей модуля сдвига в системе является паскаль (Па), хотя обычно он выражается в гигапаскалях (ГПа) или тысячах фунтов на квадратный дюйм (ksi). Ее мерная форма есть М 1 л -1 Т -2 , заменив силы
на
массовые
времена
ускорения
.
Объяснение [ править ]
| Материал | Типичные значения модуля сдвига (ГПа) (при комнатной температуре) |
| Бриллиант [2] | 478,0 |
| Сталь [3] | 79,3 |
| Утюг [4] | 52,5 |
| Медь [5] | 44,7 |
| Титан [3] | 41,4 |
| Стекло [3] | 26,2 |
| Алюминий [3] | 25,5 |
| Полиэтилен [3] | 0,117 |
| Резина [6] | 0,0006 |
| Гранит [7] [8] | 24 |
| Сланец [7] [8] | 1.6 |
| Известняк [7] [8] | 24 |
| Мел [7] [8] | 3,2 |
| Песчаник [7] [8] | 0,4 |
| Дерево | 4 |
Модуль сдвига — это одна из нескольких величин для измерения жесткости материалов. Все они возникают в обобщенном законе Гука :
- Модуль Юнга E
описывает реакцию деформации материала на одноосное напряжение в направлении этого напряжения (например, натягивание концов проволоки или размещение груза на вершине колонны, при этом проволока становится длиннее, а колонна теряет высоту). - в коэффициент Пуассона ν
описывает отклик в направлениях , ортогональных к этому одноосного напряжения (проволоки становится тоньше и толще колонны), - объемный модуль упругости К
описывает реакцию материала к (однородной) гидростатического давления (например , давление на дне океана или глубокий бассейн), - модуль сдвигаG
описывает отклик материала к напряжению сдвига (как резок его с тупыми ножницами). Эти модули не являются независимыми, и для изотропных материалов они связаны уравнениями . [9] 2 G ( 1 + ν ) = E = 3 K ( 1 − 2 ν ) {\displaystyle 2G(1+\nu )=E=3K(1-2\nu )}
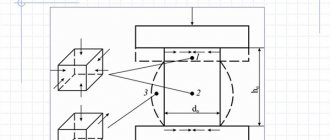
Модуль сдвига связан с деформацией твердого тела, когда оно испытывает силу, параллельную одной из его поверхностей, в то время как его противоположная сторона испытывает противодействующую силу (например, трение). Если объект имеет форму прямоугольной призмы, он деформируется в параллелепипед . Анизотропные материалы, такие как дерево , бумага, а также практически все монокристаллы, демонстрируют различную реакцию материала на напряжение или деформацию при испытании в разных направлениях. В этом случае может потребоваться использовать полное тензорное выражение упругих констант, а не одно скалярное значение.
Одно из возможных определений жидкости — это материал с нулевым модулем сдвига.
Уравнение модуля сдвига
Модуль сдвига определяется путем измерения деформации твердое тело от приложения силы, параллельной одной поверхности твердого тела, в то время как противоположная сила действует на его противоположную поверхность и удерживает твердое тело на месте. Думайте о сдвиге как о толкании одной стороны блока с трением как противодействующей силе. Другой пример — попытка отрезать проволоку или волосы тупыми ножницами.
Уравнение для модуля сдвига:
G = τ xy /γ xy = F/A/Δx/l = Fl/AΔx
Где:
- G — модуль сдвига или модуль жесткости
- τ xy — напряжение сдвига
- γ xy — деформация сдвига
- A — площадь, на которую действует сила
- Δx — поперечное смещение
- l — начальная длина
Деформация сдвига равна Δx/l = tan θ или иногда = θ, где θ — угол, образованный деформацией, вызванной приложенной силой.
Деформация – безразмерное число
Применение понятия «деформация» позволяет количественно описывать изменения размеров и формы тела, которые возникают при приложении напряжений, которые, в свою очередь, возникают при приложении некоторой нагрузки. Важно отметить, что деформация – это «чистое», безразмерное число. У деформации нет каких-либо единиц измерения. Чтобы вычислить деформацию нужно сравнить начальные, исходные размеры или форму тела до приложения нагрузки с теми же размерами или формой того же тела под нагрузкой.
Формула, по которой вычисляют деформацию, имеет величины одной и той же размерности (метры, сантиметры, миллиметры) как в знаменателе, так и в числителе. Поэтому, понятно еще из школьной физики, что эти размерные единицы взаимно сокращаются, и в результате мы получаем безразмерное число. Эта процедура хорошо видна при вычислении напряжений и деформаций для простого испытания на растяжение.
Общие понятия
Модуль упругости (модуль Юнга) — это показатель механического свойства материала, характеризующий его сопротивляемость деформации растяжения. Иными словами, это значение пластичности материала. Чем выше значения модуля упругости, тем меньше будет какой-либо стержень растягиваться при иных равных нагрузках (площадь сечения, величина нагрузки и другие).
Модуль Юнга в теории упругости обозначается буквой Е. Он является составляющей закона Гука (о деформации упругих тел). Эта величина связывает возникающее в образце напряжение и его деформацию.
Измеряется эта величина согласно стандартной международной системе единиц в МПа (Мегапаскалях). Но инженеры на практике больше склоняются к применению размерности кгс/см2.
Опытным путём осуществляется определение этого показателя в научных лабораториях. Сутью этого метода является разрыв гантелеобразных образцов материала на специальном оборудовании. Узнав удлинение и натяжение, при которых образец разрушился, делят переменные данные друг на друга. Полученная величина и является модулем (Юнга) упругости.
Таким образом определяется только модуль Юнга материалов упругих: медь, сталь и прочее. А материалы хрупкие сжимают до того момента, пока не появятся трещины: бетон, чугун и им подобные.
Диаграмма растяжения
Инженерное напряжение σ, которое применяют на диаграмме напряжение-деформация на рисунке 2, является средним или номинальным напряжением в разрывном образце. Его получают путем деления величины нагрузки F на исходную – не нагруженную – площадь А0 поперечного сечения этого образца.
σ = F/A0.
Рисунок 2 – Инженерная диаграмма напряжение-деформация. Чаще ее называют диаграммой растяжения. Пересечение пунктирной линии с диаграммой напряжение-деформация дает величину предела текучести при остаточной деформации, обычно, 0,2 %.
По мере увеличения напряжения в разрывном образце расстояние между метками базовой длины изменяется под воздействием приложенных напряжений. Результирующая деформация ɛ, которая указана на инженерной диаграмме напряжение-деформация, является средней или номинальной линейной – одноосной – деформацией. Величину этой деформации получают путем деления изменения базовой длины образца δ на исходную базовую длину образца L0:
ɛ = δ/L0 = ΔL/L0 = (L — L0)/L0
Поскольку и инженерное напряжение (σ) и деформация (ɛ) получены путем деления нагрузки на образец и удлинения образца на одну и ту же постоянную величину L0, то форма диаграммы нагрузка-удлинение и напряжение-деформация имеют одинаковую форму.
Форма и размеры диаграммы растяжения стали зависит от:
- химического состава стали,
- виде термической обработки,
- режимов пластического деформирования,
- скорости нагружения,
- температуры и
- напряженного состояния в ходе испытания на растяжение.
Механические свойства стали чаще всего определяют именно путем испытания растяжение, которое описано выше. Характеристики стали, которые обычно применяют для описания диаграммы растяжения конкретной стали включают:
- предел прочности (временное сопротивление разрыву),
- предел текучести,
- удлинение базовой длины образца (в процентах),
- сужение площади поперечного сечения образца (в процентах).
Различные типы испытаний, которые включают применение различных нагрузок на стальной образец, применяют также для определения других механических свойств стали. Примерами таких механических свойств стали являются модуль упругости, твердость, сопротивление усталости и ударная вязкость.
Влияние температуры и давления
Как и следовало ожидать, реакция материала на приложенную силу изменяется в зависимости от температуры и давления. В металлах модуль сдвига обычно уменьшается с повышением температуры. Жесткость уменьшается с увеличением давления. Для прогнозирования влияния температуры и давления на модуль сдвига используются три модели: модель напряжения пластического течения при механическом пороговом напряжении (MTS), модель модуля сдвига Надаля и Лепоака (NP) и модуль сдвига Стейнберга-Кохрана-Гинана (SCG). модель. Для металлов обычно существует область температуры и давления, в которой изменение модуля сдвига является линейным. За пределами этого диапазона поведение моделирования сложнее.
Изотропные и анизотропные материалы
Некоторые материалы изотропны по отношению к сдвигу, что означает, что деформация в ответ на силу одинакова независимо от ориентации. Другие материалы анизотропны и по-разному реагируют на напряжение или деформацию в зависимости от ориентации. Анизотропные материалы гораздо более восприимчивы к сдвигу по одной оси, чем по другой. Например, рассмотрим поведение деревянного блока и то, как он может реагировать на силу, приложенную параллельно волокну древесины, по сравнению с его реакцией на силу, приложенную перпендикулярно волокну. Рассмотрим, как алмаз реагирует на приложенную силу.. Скорость сдвига кристалла зависит от ориентации силы по отношению к кристаллической решетке.
Все механические свойства стали
Почти полный список механических свойств для стали включает:
- Твердость. Мера сопротивления вдавливанию
- Линейные коэффициенты упругости для растягивающих, сжимающих и сдвиговых нагрузок
- Предел текучести (при растягивающих, сжимающих и сдвиговых нагрузках). Показывает уровень напряжения, при котором возникают необратимые пластические деформации
- Предел прочности (при растягивающих, сжимающих и сдвиговых нагрузках). Показывает максимальные инженерные напряжения, которые материал может выдержать без разрушения. Предел прочности при растяжении – временное сопротивление разрыву – обычно связывают с началом образования шейки на разрывном образце (см. рисунок 2)
- Усталостная прочность. Показывает уровень циклических напряжений, которые вызывают разрушение из-за усталости металла после определенного количества циклов нагружения, например, 1 миллион
- Ударная вязкость. Показывает уровень поглощения ударной энергии от нагрузок, которые способен поглотить металл до разрушения
- Вязкость разрушения. Показывает уровень сопротивления разрушению, когда в изделии присутствуют дефекты и концентраторы напряжений
- Сопротивление высокотемпературной ползучести и разрушению.
- Износостойкость.
Как определить модуль упругости стали
Выяснить модули упругости для различных марок стали можно несколькими путями:
- по справочным данным из таблиц;
- экспериментальными методами для небольшого образца;
- расчетными методами, зная необходимые данные.
Жесткость стали зависит от ее химического состава и вида кристаллической решетки, от плотности, достигнутой в результате обработки. Прочность же ее конструкций определяется такими важными факторами, как параметры изделия, в том числе габариты, эксплуатационные нагрузки, и их длительность. При расчетах, выполняемых по нормированным методикам, результат осознанно завышают, чтобы предупредить возможные аварии и поломки.
Тем не менее, устойчивость стали к деформации определяется изначально ее маркой, то есть наличием примесей в сплаве.
В таблице приведены модули упругости стали наиболее популярных марок, а модуль сдвига ее составляет – 80-81 ГПа.
| Сталь | Модуль (Е), ГПа |
| углеродистая | 195-205 |
| легированная | 206-235 |
| Ст.3, Ст.5 | 210 |
| сталь 45 | 200 |
| 25Г2С, 30ХГ2С | 200 |
Из таблицы видно, что наименьшее значение прочности у стали 45, 25Г2С, 30ХГ2С, а у нержавеющей стали самое высокое – 235 ГПа.
Экспериментальный метод определения заключается в определении относительного удлинения небольшого стального образца на установке, с последующим расчетом.
В основе метода лежит заключение, что растяжение образца стали до предела упругости, подчиняется закону Гука (1). Зная приложенную силу (F) и площадь детали (А), выяснив ее удлинение (Δl) можно рассчитать Е:
Расчеты ведут в мм и МПа.
Для проектирования конструкций необходимо всегда знать или просчитывать не менее двух разных модулей упругости. Исходя из коэффициента жесткости можно перейти к другим видам сопротивления к воздействию извне для стали: упругости при изгибе и объемной.