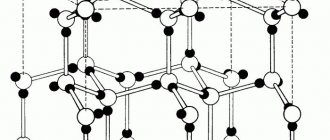
One of the most common materials that people have always preferred to work with has been metal. In each era, preference was given to different types of these amazing substances. Thus, the IV-III millennium BC is considered the Chalcolithic, or Copper Age. Later it is replaced by bronze, and then the one that is still relevant today comes into force - iron.
Today it is generally difficult to imagine that it was once possible to do without metal products, because almost everything, from household items, medical instruments to heavy and light equipment, consists of this material or includes individual parts from it. Why did metals manage to gain such popularity? Let’s try to figure out what the features are and how this is inherent in their structure.
Bravais lattices
Three Bravais lattices in a cubic crystal system:
| Bravais lattice | Primitive cubic | Body-centered cubic | Face-centered cubic |
| Pearson symbol | cP | cI | cF |
The cube primitive (cP) system consists of one lattice point at each corner of the cube. Each atom at a lattice point is then divided equally between eight adjacent cubes, and so the unit cell contains just one atom (1 ⁄ 8 × 8).
A body-centered cubic system (cI) has one lattice point at the center of the unit cell in addition to eight corner points. It has a total of 2 lattice points per unit cell (1 ⁄ 8 × 8 + 1).
A face-centered cubic system (cF) has lattice points on the faces of the cube, each contributing exactly half of the contribution in addition to the corner lattice points, giving a total of 4 lattice points per unit cell (1 ⁄ 8 × 8 from the corners plus 1 ⁄ 2 × 6 from the faces). Each sphere in the cF lattice has a coordination number of 12. The coordination number is the number of nearest neighbors of the central atom in the structure.
The face-centered cubic system is closely related to the hexagonal close-packed (hcp) system, where the two systems differ only in the relative arrangement of their hexagonal layers. the plane of the face-centered cubic system is a hexagonal mesh.
Trying to create a C-centered cubic crystal system (i.e. placing an extra lattice point at the center of each horizontal face) will result in a simple tetragonal Bravais lattice.
Types of crystal lattices
Fourteen lattice structure options are usually combined into three main types. They are as follows:
- Body-centered cubic.
- Hexagonal close-packed.
- Face-centered cubic.
The crystal structure of metals was studied only through electron microscopy, when it became possible to obtain high magnification images. And the classification of types of lattices was first given by the French scientist Bravais, by whose name they are sometimes called.
Defects in the crystal structure of metals
However, all types of cells considered may also have natural shortcomings, or so-called defects. This may be due to various reasons: foreign atoms and impurities in metals, external influences, and so on.
Therefore, there is a classification that reflects the defects that crystal lattices may have. Chemistry as a science studies each of them in order to identify the cause and method of elimination so that the properties of the material are not changed. So, the defects are as follows.
- Spot. They come in three main types: vacancies, impurities or dislocated atoms. They lead to deterioration of the magnetic properties of the metal, its electrical and thermal conductivity.
- Linear or dislocation. There are edge and screw ones. They deteriorate the strength and quality of the material.
- Surface defects. Affects the appearance and structure of metals.
Currently, methods have been developed to eliminate defects and obtain pure crystals. However, it is not possible to completely eradicate them; an ideal crystal lattice does not exist.
Vir–Phelan structure
Veer–Phelan structure
B The Veer–Phelan structure has Pm3n (223) symmetry.
It has 3 orientations of stacked tetradecahedrons involving pyritohedral cells in the gaps. It occurs as a crystal structure in chemistry where it is commonly known as the "Type I clathrate structure". Gas hydrates formed by methane, propane and carbon dioxide at low temperatures have a structure in which water molecules lie at the nodes of the Wear–Phelan structure and are hydrogen bonded together, and larger gas molecules are trapped in polyhedral cages.
The importance of knowledge about the crystalline structure of metals
From the above material, it is obvious that knowledge about the fine structure and structure makes it possible to predict the properties of the material and influence them. And the science of chemistry allows you to do this
The 9th grade of a general education school places emphasis in the learning process on developing in students a clear understanding of the importance of the fundamental logical chain: composition - structure - properties - application
Information about the crystalline structure of metals very clearly illustrates this dependence and allows the teacher to clearly explain and show children how important it is to know the fine structure in order to correctly and competently use all the properties
Periodic table and metals
In the 19th century, thanks to his brilliant mind and many years of work, Dmitry Ivanovich Mendeleev compiled a table, collecting all the chemical elements known at that time. Each of them is assigned a specific position in the table in accordance with the number of protons in the atomic nucleus. The entire table is divided into 7 periods (horizontal rows) and 8 groups (vertical rows). The longer the period, the larger the radius of the atom of the corresponding element, and the higher its valence electrons are located in orbitals. On the contrary, the older the group (movement along the table from left to right), the more valence electrons are in the last orbital and the smaller the radius of the atom.
Any element of the table can be conditionally classified as either metals or non-metals. The metals are located on the left side of the boron (B) – polonium (Po) diagonal. If you look at the table, you can immediately understand that the number of metals is several times greater than the number of non-metals.
Read also: Homemade viscometer for paint
Polymorphism
Quartz is one of several crystalline forms of silica, SiO 2 . The most important forms of silica include: α-quartz, β-quartz, tridymite, cristobalite, coesite, and stishovite.
Polymorphism is the appearance of several crystalline forms of a material. It is found in many crystalline materials, including polymers, minerals, and metals. According to Gibbs' rules of phase equilibrium, these unique crystalline phases depend on intense variables such as pressure and temperature. Polymorphism is related to allotropy, which refers to elemental solids. The overall morphology of a material is described by polymorphism and other variables such as crystal habit, amorphous fraction, or crystallographic defects. Polymorphs have varying stabilities and can spontaneously and irreversibly transform from a metastable form (or thermodynamically unstable form) to a stable form at a certain temperature. They also have different melting points, solubility, and X-ray diffraction patterns.
A good example of this is the quartz form of silicon dioxide or SiO 2 . In the vast majority of silicates, the Si atom has a tetrahedral coordination over 4 oxygen atoms. All but one crystalline form contains tetrahedral {SiO 4 } units linked together by common vertices in different arrangements. In different minerals, tetrahedra exhibit varying degrees of networking and polymerization. For example, they occur singly, linked together in pairs, into larger finite clusters, including rings, chains, double chains, sheets, and three-dimensional frameworks. Minerals are classified into groups based on these structures. In each of the 7 thermodynamically stable crystalline forms or polymorphs of crystalline quartz, only 2 of the 4 edges of the {SiO 4 } tetrahedra are shared with the others, giving the pure chemical formula of silica: SiO 2 .
Another example is elemental tin (Sn), which is ductile at ambient temperatures but brittle when cooled. This change in mechanical properties is due to the existence of its two main allotropes, α- and β-tin. Two allotropes that occur at normal pressure and temperature, α-tin and β-tin, are better known as gray tin
and
white tin
respectively. Two further allotropes, γ and σ, exist at temperatures above 161 °C and pressures above several GPa. White tin is metallic and is a stable crystalline form at room temperature or above. Below 13.2 °C, tin exists in a gray form that has a cubic diamond crystal structure, similar to diamond, silicon, or germanium. Gray tin has no metallic properties at all, is a dull gray powdery material, and has few uses other than a few specialized semiconductor applications. Although the α–β transformation temperature of tin is nominally 13.2 °C, impurities (e.g. Al, Zn, etc.) lower the transition temperature well below 0 °C, and with the addition of Sb or Bi the transformation may not occur at all.
Crystallographic uses
In a crystal structure, the geometric model of an atom is a geometric structure of atomic coordination, where the definition of atomic coordination depends on the bonds in the model.
For example, in rock salt, the ionic composition of each sodium atom contains the six nearest neighboring chloride ions in octahedral geometry, and each chloride similarly contains six neighboring sodium ions in octahedral geometry. In metals with a body-centered structure, each atom has a bond with eight nearby other atoms with cubic geometry. In metals with a face-centered cubic structure, each atom has twelve bonds to neighboring atoms with cuboctahedral geometry. Coordination Geometry Table
| Coordination number | Geometry | Image | Examples of discrete (finite) complexes | Examples on crystals |
| 2 | linear | Ag(CN)2− to KAg(CN)2 | Ag in silver cyanide, Au in AuI | |
| 3 | flat triangle | Cu(CN)32− in Na2Cu(CN)3 3H2O | O in TiO2 (rutile structure) | |
| 4 | tetrahedron | CoCl42− | Zn and S in zinc sulfide, Si in silicon dioxide | |
| 4 | square | AgF4− | CuO | |
| 5 | trigonal bipyramidal | SnCl5− | ||
| 5 | square pyramidal | InCl52− in (NEt4)2InCl5 | ||
| 6 | octahedron | Fe(H2O)62+ | Na and Cl in sodium chloride | |
| 6 | trigonal prismatic | Mo(SCHCHS)3 | As to NiAs, Mo to MoS2 | |
| 7 | pentagonal bipyramidal | ZrF73− in (NH4)3ZrF7 | Pa to PaCl5 | |
| 7 | face-centered octahedral | [HoIII(PhCOCHCOPh)3(H2O)] | La to La2O3 | |
| 7 | trigonal prismatic, quadratic monoface-centered | TaF72− to K2TaF7 | ||
| 8 | cube | Cesium chloride, calcium fluoride | ||
| 8 | square anti-prismatic | TaF83− in Na3TaF8 | Thorium(IV) chloride | |
| 8 | Mo(CN)84− in K4[Mo(CN)8].2H2O | Zr to K2ZrF6 | ||
| 8 | hexagonal bipyramidal | N to Li3N | ||
| 8 | octahedron | Ni in nickel arsenide | ||
| 8 | Ca to CaFe2O4 | |||
| 8 | trigonal prismatic, square face double-ribbed | PuBr3 | ||
| 9 | trigonal prismatic, square obverse triribbed | [ReH9]2− in potassium nonahydrorenate | SrCl2 6H2O, Th in RbTh3F13 | |
| 9 | English monocapped square antiprismatic | [Th(thoropolonate)4(H2O)] | La in LaTe2 | |
| 10 | English bicapped square antiprismatic | Th(C2O4)42− | ||
| 11 | Th in [ThIV(NO3)4(H2O)3] (NO3−) | |||
| 12 | icosahedron | Th in Th(NO3)62− ion in Mg[Th(NO3)6] 8H2O | ||
| 12 | cuboctahedron | ZrIV(η³−(BH4)4) | ||
| 12 | ||||
| 14 | double-rib anti-prismatic hexagonal | U(BH4)4 |
Where there are no discrete complexes means that the compounds are found as individual units of spheres around atoms in crystals
References
- ^ a b c
P. M. de Wolf, N. V. Belov, E. F. Berto, M. J. Burger, J. D. H. Donnay, W. Fischer, T. Khan, V. A. Koptsik , A. L. McKay, H. Vondracek, A. J. C. Wilson, and S. K. Abrahams (1985).
“Nomenclature of crystal families, Bravais lattice types and arithmetic classes. Report of the Special Committee of the International Union of Crystallography on Symmetry Nomenclature." Acta Crystallographica Section
A.
41
(3): 278. doi:10.1107/S0108767385000587.CS1 maint: several names: list of authors (link to site) - Prince, E., ed. (2006). International Tables for Crystallography
. International Union of Crystallography. Doi:10.1107/97809553602060000001. ISBN 978-1-4020-4969-9. - Crystallography and Minerals Ordered by Crystal Form
, Webmineral - Greenwood, Norman N.; Earnshaw, Alan (1997). Chemistry of elements
(2nd ed.). Butterworth-Heinemann. ISBN 978-0-08-037941-8. - The initial discovery was made in J. Chem. Phys. 14
, 569 (1946). - Structure of CsCl (B2) Archived 2008-09-15 on the Wayback Machine
- ^ a b
Seitz,
Modern Theory of Solids
(1940), p.49 - Structure of NaCl (B1) Archived 2008-10-19 at the Wayback Machine
- Sundquist, J. J.; Lin, K. S. (1981). "Electronic structure of the F center in a sodium fluoride crystal". Journal of Physics C: Solid State Physics
.
14
(32):4797–4805. Bibcode:1981JPhC...14.4797S. Doi:10.1088/0022-3719/14/32/016. - Abrahams, S.C.; Bernstein, J. L. (1965). “The accuracy of an automatic diffractometer. Measurement of structural factors of sodium chloride". Acta Crystallogr. 18
(5):926–932. Doi:10.1107/S0365110X65002244. - Kao, W.; Peretti, E. (1970). "Ternary subsystem Sn4As3-SnAs-SnTe". Journal of Less Common Metals
.
22
: 39–50. Doi:10.1016/0022-5088(70)90174-8. - ^ a b c
J. Aigueperse, P. Mollard, D. Devilliers, M. Chemla, R. Faron, R. Romano, J. P. Cuer, "Fluorine Compounds, Inorganic" (Section 4) in Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH , Weinheim, 2005. doi:10.1002/14356007.a11_307. - Gu, Zheng; Edgar, J. N; Pomeroy, J; Kuball, M; Coffey, D. W. (August 2004). "Crystal growth and properties of scandium nitride". Journal of Materials Science: Materials in Electronics
.
15
(8):555–559. Doi:10.1023/B: JMSE.0000032591.54107.2c. S2CID 98462001. - "Fluorite." aflow.org
. Received 2020-05-22. - "Rock salt". aflow.org
. Received 2020-05-22. - L. Kantorovich (2004). Quantum theory of solids.
. Springer. paragraph 32. ISBN 1-4020-2153-4. - Birkbeck College, University of London
- Structure of zinc blende (B3) Archived October 19, 2008 Wayback Machine
Atomic coordination
By considering the arrangement of atoms relative to each other, their coordination numbers (or number of nearest neighbors), interatomic distances, types of bonds, etc., it is possible to form a general idea of structures and alternative ways of visualizing them.
Tight packing
GPU lattice (left) and fcc lattice (right)
The principles involved can be understood by considering the most efficient way of packing spheres of equal size and stacking closely packed atomic planes in three dimensions. For example, if plane A lies below plane B, there are two possible ways of placing an additional atom on top of layer B. If the additional layer were placed directly above plane A, this would result in the following series:
…
ABABABAB
…
This arrangement of atoms in a crystal structure is known as hexagonal close packing (hcp)
.
If, however, all three planes are staggered relative to each other and the sequence is repeated only after the fourth layer is located directly above plane A, then the following sequence occurs:
…
ABCABCABC
…
This type of structural arrangement is known as cubic close packing (ccp)
.
The unit cell of the ccp arrangement of atoms is the face-centered cubic (fcc) unit cell. This is not immediately obvious, since the close-packed layers are parallel to the {111} planes of the fcc unit cell. There are four different orientations of the close-packed layers.
Packaging efficiency
can be worked out by calculating the total volume of the spheres and dividing by the cell volume as follows:
4×43πр3162р3π32π320.7405 …{\displaystyle {\frac {4\times {\frac {4}{3))\pi r^{3 }} {16 {\sqrt {2}}r^{3}}} = {\frac {\pi}{3{\sqrt {2}}}} = 0.7405...} 74
% packaging efficiency is the maximum density possible for unit cells constructed from spheres of only one size. Most crystalline forms of metal elements are hcp, fcc or bcc (body centered cubic). The coordination number of atoms in the hcp and fcc structure is 12 and its atomic packing factor (PF) is the number mentioned above, 0.74. This can be compared with the APF of the bcc structure of 0.68.
Multi-element connections
Compounds consisting of more than one element (such as binary compounds) often have crystal structures based on the cubic crystal system. Some of the most common ones are listed here.
Structure of cesium chloride
And cesium chloride cell.
The two colors of the spheres represent the two types of atoms. In the cosmic group of cesium chloride (CsCl), the structure is called Pm3m (in Hermann–Mauguin notation) or "221" (in the International Tables for Crystallography). In Strukturbericht the designation is "B2".[6]
One structure is the "interpenetrating primitive cubic" structure, also called the "cesium chloride" structure. Each of the two types of atoms forms a separate primitive cubic lattice, with an atom of one type at the center of each cube of the other type. In the unit cell of CsCl, each ion is located in the center of a cube of ions of the opposite type, so the coordination number is eight. The overall arrangement of atoms is the same as that of a body-centered cubic, but with alternating types of atoms at different lattice sites. On the other hand, this lattice could be viewed as a simple cubic structure with a secondary atom in a cubic void.
Besides cesium chloride itself, the structure also appears in several other alkali metal halides when prepared at low temperatures or high pressure.[7] In general, this structure is more likely to be formed from two elements whose ions are approximately the same size (for example, the ionic radius of Cs+ = 167 pm and Cl− = 181 pm).
The coordination number of each atom in the structure is 8: the central cation is coordinated to the 8 anions at the corners of the cube as shown, and similarly, the central anion is coordinated to the 8 cations at the corners of the cube.
Other compounds having a structure similar to cesium chloride: CsBr, CsI, high temperature RbCl, AlCo, AgZn, BeCu, MgCe, RuAl and SrTl. [ citation needed
]
Structure of rock salt
Crystal structure of rock salt.
Each atom has six nearest neighbors, with an octahedral geometry. The cosmic structure group of rock salt (NaCl) is called Fm3m (in Hermann–Mauguin Notation) or "225" (in the International Tables for Crystallography). In Strukturbericht the designation is "B1".[8]
In rock salt or sodium chloride (halite), each of the two types of atoms forms a separate face-centered cubic lattice, with the two lattices intersecting each other to form a three-dimensional checkerboard pattern. Alternatively, one could view this structure as a face-centered cubic structure with secondary atoms in its octahedral holes.
Examples of compounds with this structure include sodium chloride itself, along with almost all other alkali metal halides, and "many oxides, sulfides, selenides and tellurides of the divalent metals".[7] More generally, this structure is more likely to form if the cation is somewhat smaller than the anion (cation/anion radius ratio between 0.414 and 0.732).
The coordination number of each atom in this structure is 6: each cation is coordinated to 6 anions at the vertices of the octahedron, and similarly each anion is coordinated to 6 cations at the vertices of the octahedron.
Interatomic distance (the distance between the cation and the anion, or half the length of the unit cell a
) in some crystals with a rock salt structure: 2.3 Å (2.3 × 10−10 m) for NaF,[9] 2.8 Å for NaCl,[10] and 3.2 Å for SnTe.[11]
Other compounds that have a structure similar to rock salt are LiF,[12] LiCl, LiBr, LiI, NaF,[12] NaBr, NaI, KF,[12] KCl, KBr, KI, RbF, RbCl, RbBr, RbI, CsF, MgO, PbS, AgF, AgCl, AgBr[ quote needed
] and ScN.[13]
The fluorite structure and antifluorite structures (AB2) are also Fm3m structures, but have a 1:2 ion ratio. They are designated Wyckoff positions 4a and 8c, whereas the rock salt structure positions are 4a and 4b.[14][15]
Structure of zinc blende
Zinc blende unit cell
The cosmic group of the zinc blende structure is called F43 m (Herman–Mauguin Designation inch) or 216.[16][17] The Strukturbericht designation is "B3".[18]
The zinc blende structure (also called "zinc blende") is named after the mineral zinc blende (sphalerite), a form of zinc sulfide (β-ZnS). As in the structure of rock salt, the two types of atoms form two interpenetrating face-centered cubic lattices. However, it differs from the structure of rock salt in the way the two lattices are positioned relative to each other. The structure of zinc blende has a tetrahedral coordination: The nearest neighbors of each atom consist of four atoms of opposite types, arranged as the four vertices of a regular tetrahedron. In general, the arrangement of atoms in a zinc blende structure is the same as a cubic diamond structure, but with alternating types of atoms at different lattice sites.
Examples of compounds with this structure include zinc blende itself, lead(II) nitrate, many complex semiconductors (such as gallium arsenide and cadmium telluride), and many other binary compounds.
Other compounds exhibiting a structure similar to zinc blende are α-AgI, β-BN, diamond, CuBr, β-CdS, BP, and BA.[ citation needed
]
Presence of order in the arrangement of particles
In an amorphous substance, unlike a crystalline one, there is no order in the arrangement of particles. If in a crystalline substance you mentally connect two atoms close to each other with a straight line, then you can find that the same particles will lie on this line at strictly defined intervals:
Thus, in the case of crystalline substances, we can talk about such a concept as a crystal lattice.
A crystal lattice is a spatial framework that connects the points in space in which the particles that form the crystal are located.
The points in space at which the particles forming a crystal are located are called nodes of the crystal lattice.
Depending on which particles are located at the nodes of the crystal lattice, there are: molecular, atomic, ionic and metal crystal lattices.
At the sites of a molecular crystal lattice Crystal lattice of ice Crystal lattice of ice as an example of a molecular lattice
There are molecules within which the atoms are connected by strong covalent bonds, but the molecules themselves are held near each other by weak intermolecular forces. Due to such weak intermolecular interactions, crystals with a molecular lattice are fragile. Such substances differ from substances with other types of structure by significantly lower melting and boiling points, do not conduct electric current, and may or may not dissolve in various solvents.
Solutions of such compounds may or may not conduct electric current, depending on the class of the compound. Compounds with a molecular crystal lattice include many simple substances - nonmetals (hardened H2, O2, Cl2, orthorhombic sulfur S8, white phosphorus P4), as well as many complex substances - hydrogen compounds of nonmetals, acids, oxides of nonmetals, most organic substances. It should be noted that if a substance is in a gaseous or liquid state, it is inappropriate to talk about a molecular crystal lattice: it is more correct to use the term molecular type of structure.
crystal lattice of diamond Crystal lattice of diamond as an example of an atomic lattice At the nodes of an atomic crystal lattice
there are atoms. Moreover, all the nodes of such a crystal lattice are “linked” together through strong covalent bonds into a single crystal. In fact, such a crystal is one giant molecule. Due to their structural features, all substances with an atomic crystal lattice are solid, have high melting points, are chemically inactive, insoluble in either water or organic solvents, and their melts do not conduct electric current. It should be remembered that substances with an atomic type of structure include boron B, carbon C (diamond and graphite), silicon Si from simple substances, and silicon dioxide SiO2 (quartz), silicon carbide SiC, boron nitride BN from complex substances.
In substances with an ionic crystal lattice, lattice sites contain ions connected to each other through ionic bonds.
Since ionic bonds are quite strong, substances with an ionic lattice have relatively high hardness and refractoriness. Most often, they are soluble in water, and their solutions, like melts, conduct electric current. Substances with an ionic crystal lattice include metal and ammonium salts (NH4+), bases, and metal oxides. A sure sign of the ionic structure of a substance is the presence in its composition of both atoms of a typical metal and a non-metal.
Crystal lattice of sodium chloride
The crystal lattice of sodium chloride as an example of an ionic lattice. However, it should be noted that in substances with an ionic type of structure, in addition to ionic ones, covalent polar bonds can often be found. This is observed in the case of complex ions, i.e. consisting of two or more chemical elements (SO42-, NH4+, PO43-, etc.). Within such complex ions, the atoms are linked to each other by covalent bonds.
Metal crystal lattice
observed in crystals of free metals, for example, sodium Na, iron Fe, magnesium Mg, etc. In the case of a metal crystal lattice, its nodes contain cations and metal atoms, between which electrons move. In this case, moving electrons periodically attach to cations, thus neutralizing their charge, and individual neutral metal atoms in return “release” some of their electrons, turning, in turn, into cations. In fact, “free” electrons do not belong to individual atoms, but to the entire crystal.
Structure Prediction
The difficulty of predicting stable crystal structures based on knowledge of chemical composition alone has long been a stumbling block to fully computational materials design. Now, thanks to more powerful algorithms and high-performance computing, structures of moderate complexity can be predicted using approaches such as evolutionary algorithms, random sampling, or metadynamics.
The crystal structures of simple ionic solids (such as NaCl or table salt) have long been rationalized in terms of Pauling's rules, first stated in 1929 by Linus Pauling, whom many have since called the "father of chemical bonding". Pauling also considered the nature of interatomic forces in metals and concluded that about half of the five d orbitals in transition metals are involved in bonding, with the remaining nonbonding d orbitals responsible for magnetic properties. In this way, he was able to relate the number of d-orbitals in bond formation to bond length, as well as many physical properties of the substance. He subsequently introduced the metal orbital, an additional orbital needed to allow unlimited valence bond resonance between different electronic structures.
In resonance valence bond theory, the factors that determine the choice of one of the alternative crystal structures of a metal or intermetallic compound revolve around the resonance energy of the bonds between interatomic positions. It is clear that some resonance modes will contribute more (be more mechanically stable) than others, and that in particular the simple ratio of the number of bonds to the number of positions will be exceptional. The resulting principle is that special stability is associated with the simplest ratios or "bond numbers": 1 ⁄ 2, 1 ⁄ 3, 2 ⁄ 3, 1 ⁄ 4, 3 ⁄ 4, etc. The choice of structure and value of the axial ratio ( which determines the relative bond lengths), is thus the result of an atom's efforts to use its valency in forming stable bonds with prime fractional bond numbers.
Postulating a direct correlation between electron concentration and crystal structure in beta-phase alloys, Hume-Rothery analyzed trends in melting points, compressibility, and bond lengths as a function of group number in the periodic table to establish the valence system of transition elements in the metallic state. Thus, this treatment emphasized an increase in bond strength as a function of group number. The effect of directional forces was highlighted in one paper on the connection between bonding hybrids and metallic structures. The resulting correlation between electronic and crystal structures is summarized by one parameter, the weight of d electrons per hybridized metal orbital. The “D-weight” is 0.5, 0.7 and 0.9 for the fcc, hcp and bcc structures, respectively. Thus, the connection between d electrons and the crystal structure becomes apparent.
When predicting/modeling a crystal structure, periodicity is usually applied since the system appears to be indefinitely large in all directions. Starting from a triclinic structure with no additional assumed symmetry properties, the system can be made to show some additional symmetry properties by applying Newton's Second Law to the particles in the unit cell and a recently developed dynamical equation for the system's period vectors (lattice parameters including angles), even if the system is subjected to external loads
Volume
The volume of a unit cell is determined depending on its geometric shape. For the cubic system, it is calculated as the length of the face (the center-to-center distance of the atoms) raised to the third power. For the hexagonal system, the volume can be determined using the formula given below:
where a and c are the crystal lattice parameters, measured in angstroms.
In practice, the parameters of the crystal lattice are calculated so that in the future it is possible to determine the structure of the compound, the mass of the atom (based on the weight of a given volume and Avogadro’s number) or its radius.
Reciprocal lattices of various crystals
The reciprocal lattices for the cubic crystal system are as follows.
Simple cubic lattice
A simple cubic Bravais lattice with a cubic primitive cell side has as its reverse side a simple cubic lattice with a cubic primitive cell side (in the crystallographer's definition). Therefore, a cubic lattice is called self-dual, having the same symmetry in reciprocal space as in real space. a{\displaystyle a}2πa{\displaystyle \textstyle {\frac {2\pi }{a))}1a{\displaystyle \textstyle {\frac {1}{a))}
Face-centered cubic (fcc) lattice
The reciprocal lattice for an fcc lattice is a body-centered cubic (bcc) lattice with a cube side. 4πa{\displaystyle \textstyle {\frac {4\pi }{a))}
Consider the FCC composite unit cell. Find the primitive FCC unit cell; those. unit cell with one lattice point. Now let's take one of the vertices of a primitive unit cell as the origin of coordinates. Give the basis vectors of a real lattice. Then, using known formulas, the basis vectors of the reciprocal lattice can be calculated. These FCC reciprocal lattice vectors represent the basis vectors of the real BCC lattice
Note that the basis vectors of the real bcc lattice and the reciprocal fcc lattice are similar to each other in direction, but not in magnitude.
Body-centered cubic (bcc) lattice
The reciprocal lattice of a bcc lattice is a fcc lattice with a cube side. 4πa{\displaystyle \textstyle {\frac {4\pi }{a))}
It can be easily proven that only Bravais lattices with an angle of 90 degrees between them (cubic, tetragonal, rhombic) have vectors parallel to their vectors in real space. (a1,a2,a3){\displaystyle \left (\mathbf {a} _{1},\mathbf {a} _{2},\mathbf {a} _{3}\right)}(b1,b2 ,b3){\displaystyle \left (\mathbf {b} _{1},\mathbf {b} _{2},\mathbf {b} _{3}\right)}
Simple hexagonal lattice
The inverse of Brava's simple hexagonal lattice with lattice constant c and another simple hexagonal lattice with lattice constant and rotated 30° around the c axis relative to the straight lattice. Therefore, a simple hexagonal lattice is called self-dual, having the same symmetry in reciprocal space as in real space. vectors a 1 = (a (3) 1/2 / 2) i + (a / 2) j; a 2 = – (a (3) 1/2 / 2) i + (a / 2) j ve a 3 = ak 2πc{\displaystyle \textstyle {\frac {2\pi }{c))}4πa3{\ displaystyle \textstyle {\frac {4\pi }{a{\sqrt {3))))}
Crystal classes
The isometric crystal system
class names, point groups (in Schoenflies Notation, Hermann–Mauguin Notation, orbifold, and Coxeter Notation), type, examples, International Tables of Crystallography space group number,[2] and space groups are listed in the table below. There are 36 cubic space groups in total.
| # | Group of points | Type | example | Space groups | ||||||
| name[3] | Schön. | Intl | Sphere. | Coke. | Primitive | Center of the face | At the center of the body | |||
| 195–197 | Tetartoid | 23 | 332 | [3,3]+ | enantiomorphic | Ulmannite, Sodium Chlorate | P23 | F23 | I23 | |
| 198–199 | P213 | I213 | ||||||||
| 200–204 | Diploid | Right now | 2/m3 (m3) | 3*2 | [3+,4] | centrosymmetric | Pyrite | Evenings3, Pn3 | FM3, Fd3 | i3 |
| 205–206 | Pa3 | Ya3 | ||||||||
| 207–211 | Gyroidal | 432 | 432 | [3,4]+ | enantiomorphic | Petzite | P432, P4232 | F432, F4132 | I432 | |
| 212–214 | P4332, P4132 | I4132 | ||||||||
| 215–217 | Hexagonal | Тd | 43m | *332 | [3,3] | Sphalerite | p43m | F43m | i43m | |
| 218–220 | n43n | F43c | i43D | |||||||
| 221–230 | Hexoctahedral | Ochas | 4/m32/m (m3m) | *432 | [3,4] | centrosymmetric | Galena, Halite | Vechera3m, Mon3p, Vechera3p, Pn3m | FM3m, Fm3c, Fd3m, Fd3c | I3m, I3d |
Other terms for hexoctahedron: normal class, holohedral, ditesseral central class, galena type.
General concept of metals
"Chemistry. 9th grade" is a textbook used by schoolchildren. It is here that metals are studied in detail. A large chapter is devoted to the consideration of their physical and chemical properties, because their diversity is extremely great.
It is from this age that it is recommended to give children an idea of these atoms and their properties, because teenagers can already fully appreciate the significance of such knowledge. They see perfectly well that the variety of objects, machines and other things around them is based on a metallic nature.
What is metal? From the point of view of chemistry, these atoms are usually classified as those that have:
- a small number of electrons at the outer level;
- exhibit strong restorative properties;
- have a large atomic radius;
- As simple substances, they have a number of specific physical properties.
The basis of knowledge about these substances can be obtained by considering the atomic-crystalline structure of metals. It is this that explains all the features and properties of these compounds.
In the periodic table, most of the entire table is allocated to metals, because they form all the secondary subgroups and the main ones from the first to the third group. Therefore, their numerical superiority is obvious. The most common are:
All metals have a number of properties that allow them to be combined into one large group of substances. In turn, these properties are explained precisely by the crystalline structure of metals.
Body-centered lattice
The structure of the crystal lattice of metals of this type is the following structure. This is a cube with eight atoms at its nodes. Another one is located in the center of the free internal space of the cell, which explains the name “body-centered”.
This is one of the options for the simplest structure of the unit cell, and therefore the entire lattice as a whole. The following metals have this type:
- molybdenum;
- vanadium;
- chromium;
- manganese;
- alpha iron;
- beta iron and others.
The main properties of such representatives are a high degree of malleability and ductility, hardness and strength.
Primitive cell
A unit cell is called primitive if its particles are found only at the vertices of the lattice and are absent in other places. Its volume is minimal compared to other types. In practice, it often turns out to be low-symmetric (an example is the Wigner-Seitz cell).
In non-primitive cells, an atom in the center of the volume divides them into 2 or 4 identical parts. In the face-centered structure, there is a division into 8 parts. In metallography, the concept of an elementary cell, rather than a primitive cell, is used, since the symmetry of the former allows a more complete description of the crystalline structure of the material.
Voids in a unit cell
Visualization of a cubic diamond unit cell: 1. Unit cell components, 2. One unit cell, 3. Lattice of 3 x 3 x 3 unit cells.
A simple cubic unit cell has one cubic void at the center.
A body-centered cubic unit cell has six octahedral voids located in the center of each edge of the unit cell, and twelve additional ones located in the middle of each edge of the same cell, for a total of six octahedral voids. In addition, there are 24 tetrahedral voids spaced squarely around each octahedral void, for a total of twelve pure tetrahedral voids. These tetrahedral voids are not local maxima and are not technically voids, but they sometimes appear in polyatomic unit cells.
A face-centered cubic unit cell has eight tetrahedral voids located midway between each corner and the center of the unit cell, for a total of eight pure tetrahedral voids. In addition, there are twelve octahedral voids located at the midpoints of the edges of the unit cell, as well as one octahedral hole at the very center of the cell, for a total of four pure octahedral voids.
One important characteristic of a crystal structure is the atomic packing factor. This is calculated by assuming that all the atoms are identical spheres, with a radius large enough for each sphere to abut the next. The atomic packing factor is the fraction of space filled by these spheres.
Assuming one atom per lattice point, in a primitive cubic lattice with a cube side length a
, the radius of the ball will be 2 and the atomic packing factor turns out to be about 0.524 (which is quite low).
Similarly, in a bcc
lattice the atomic packing factor is 0.680, and in
an fcc lattice
it is 0.740.
fcc
value is the highest theoretically possible value for any lattice, although there are other lattices that also achieve the same value, such as hexagonal close-packed (
hcp
) and one version of tetrahedral
bcc
.
In general, because atoms in a solid are attracted to each other, more densely packed atoms tend to be more abundant. (Although loosely packed structures may occur, for example if orbital hybridization requires certain bond angles.) Accordingly, a primitive cubic structure with a particularly low atomic packing ratio is rare in nature, but is found in polonium. BCC
and
HCC
, with their higher densities, are both quite widespread in nature.
Examples of bcc
include iron, chromium, tungsten, and niobium.
Examples of fcc
include aluminum, copper, gold and silver.
Structure and geometry
Crystal lattices represent a collection of crystallites. In nearby grains they are mutually located at a certain angle. Atoms, which are microscopic particles of matter and the smallest parts of chemical elements, are located in crystallites in accordance with short- and long-range order. The first implies a certain order of placement and stability of the microparticles closest to each other, the second – the most distant ones. It is possible for individual atoms to leave their locations due to diffusion, but this does not lead to a violation of the order of the structure.
The type of lattice is determined by the shape of the simplest geometric body that forms it. Cubic lattices are differentiated into four types:
- cubic with microparticles in the corners;
- the body-centered version has eight atoms located at the corners and one in the center;
- a face-centered cubic lattice is distinguished by the placement of atoms at the centers of the faces and vertices;
- hexagonal close-packed with microparticles located in the corners of a hexagonal prism, in the center of the bases and three in the central plane.
The main parameters of lattices include compactness, which is understood as the degree of filling of the volume with atoms. It is determined by three other indicators:
- lattice parameter – the value of the interatomic distance in nm along the edge of the simplest cell (characterized for cubic options by the length of the edge);
- coordination number, which refers to the number of nearest neighboring microparticles;
- packing density, represented by the ratio of the total atomic volume of the lattice and its total volume.
To measure the lattice parameter, the X-ray diffraction method of analysis is used. When calculating the number of atoms, it is taken into account that each of them belongs to several cells at once. For cubic lattices, the exception is a microparticle placed in the center of the cube.
For the body-centered type, the coordination number is 8 based on the number of atoms closest to the central one. For the face-centered version, a microparticle on a cubic face is placed at the same distance from four in the corners, four on the faces, and four of the nearest crystalline cell. That is, the coordination number is 12.
Different variants of crystal lattices are characterized by different packing densities. For a simple cubic lattice, the coordination number is 6, for bcc - 8, fcc and GP (hexagonal close-packed) - 12.
For the body-centered version, the volumes of microparticles and interatomic spaces are in proportion 68/32%; for fcc, the values of the corresponding parameters are 74 and 26%, respectively. The compactness of the lattice is determined by the characteristics of the metallic electronic structure and the nature of the atomic bond.
Due to the ordering of the lattice, it is possible to identify crystallographic planes and directions.
Directions are understood as straight lines along which atoms are located. That is, they are represented by edges, diagonals and faces.
The planes are divided into diagonal and cubic planes.
Three-digit indices are used to designate these categories. For directions, they are determined by finding the nearest atom and using its coordinates relative to point O. For planes, the coordinates of the points of their intersection with the coordinate axes are found and reversed.
It should be noted that in crystalline solids there is a change in mechanical properties along the directions. This feature, called anisotropy, is explained by different atomic densities. Thus, for cubic lattices along the diagonals and on diagonal planes, this indicator is greater than along the edges and on planes passing through the faces. In this case, anisotropy is observed within a crystallite or single crystal. This is not typical for polycrystalline bodies due to the averaging of parameters in all directions for a large number of arbitrarily mutually oriented grains. In view of this, metals are classified as pseudo- or quasi-isotropic bodies.
In addition, some metals (Ti, Fe, Sn) are characterized by allotropy, which is understood as a change in the crystal structure by changing the type of the simplest cell. This property is also called polymorphism.
Thus, iron in the temperature range 911-1392 °C has a face-centered cubic lattice, and at temperatures outside the given range it has a separately-centered lattice (before melting at 1539 °C). Greek letters are used to differentiate allotropic forms.
There may be lattice defects. They are classified into several types.
- Point atoms, close in size to atoms, are represented by vacancies (empty sites, interstitial microparticles), substitutional impurity atoms (the same size as the original ones) and interstitial atoms (small microparticles in interstitial sites).
- Linear (extended) are represented by dislocations (plane displacements). They are classified into the most common edge (extraplane or half-plane) and helical (twisting planes).
- Surface – distortions at grain boundaries due to moving dislocation grains.
- Volumetric – pores and cracks.
These defects have different effects on strength. For point ones, the degree of influence on this indicator is determined by their nature and number in a specific volume. Linear defects, due to their high mobility, significantly affect the strength, simplifying the shifts of crystallites under the influence of stress. The impact of linear defects on strength is assessed by their density (the ratio of their total length to the volume of the material). Its limiting value is 1013 cm-2 (with more, destruction occurs). Based on the fact that fine-grained materials are stronger than coarse-grained materials with a larger total extent of boundaries, surface defects, on the contrary, increase strength. Volumetric, in addition to directly reducing strength, significantly increases stress from work loads, concentrating them.
Defects in the crystal structure of metals
However, all types of cells considered may also have natural shortcomings, or so-called defects. This may be due to various reasons: foreign atoms and impurities in metals, external influences, and so on.
Therefore, there is a classification that reflects the defects that crystal lattices may have. Chemistry as a science studies each of them in order to identify the cause and method of elimination so that the properties of the material are not changed. So, the defects are as follows.
- Spot. They come in three main types: vacancies, impurities or dislocated atoms. They lead to deterioration of the magnetic properties of the metal, its electrical and thermal conductivity.
- Linear or dislocation. There are edge and screw ones. They deteriorate the strength and quality of the material.
- Surface defects. Affects the appearance and structure of metals.
Currently, methods have been developed to eliminate defects and obtain pure crystals. However, it is not possible to completely eradicate them; an ideal crystal lattice does not exist.
Properties of metals
The specific properties of the substances in question include the following.
- Metallic shine. All representatives of simple substances have it, and most have the same silvery-white color. Only a few (gold, copper, alloys) are different.
- Malleability and plasticity - the ability to deform and recover quite easily. It is expressed to different degrees in different representatives.
- Electrical and thermal conductivity are one of the main properties that determine the areas of application of a metal and its alloys.
The crystalline structure of metals and alloys explains the reason for each of the indicated properties and speaks about their severity in each specific representative. If you know the features of such a structure, then you can influence the properties of the sample and adjust it to the desired parameters, which is what people have been doing for many decades.