Одним из самых распространенных материалов, с которым всегда предпочитали работать люди, был металл. В каждую эпоху предпочтение отдавалось разным видам этих удивительных веществ. Так, IV-III тысячелетия до нашей эры считаются веком хальколита, или медным. Позже его сменяет бронзовый, а затем в силу вступает тот, что и по сей день является актуальным — железный.
Сегодня вообще сложно представить, что когда-то можно было обходиться без металлических изделий, ведь практически все, начиная от предметов быта, медицинских инструментов и заканчивая тяжелой и легкой техникой, состоит из этого материала или включает в свой состав отдельные части из него. Почему же металлы сумели завоевать такую популярность? В чем проявляются особенности и как это заложено в их строении, попробуем разобраться далее.
Решетки Браве
Три решетки Браве в кубической кристаллической системе:
| Решетка Браве | Примитивная кубическая | Телоцентрированный кубический | Гранецентрированная кубическая |
| Символ Пирсона | cP | cI | cF |
Примитивная кубическая система (cP) состоит из одной точки решетки на каждом углу куба. Затем каждый атом в точке решетки поровну делится между восемью соседними кубами, и поэтому элементарная ячейка содержит всего один атом ( 1 ⁄ 8 × 8).
Объемно-центрированная кубическая система (cI) имеет одну точку решетки в центре элементарной ячейки в дополнение к восьми угловым точкам. Он имеет в сумме 2 точки решетки на элементарную ячейку ( 1 ⁄ 8 × 8 + 1).
Гранецентрированная кубическая система (cF) имеет точки решетки на гранях куба, каждая из которых дает ровно половину вклада в дополнение к угловым точкам решетки, что дает в общей сложности 4 точки решетки на элементарную ячейку ( 1 ⁄ 8 × 8 от углов плюс 1 ⁄ 2 × 6 от граней). Каждая сфера в решетке cF имеет координационное число 12. Координационное число – это число ближайших соседей центрального атома в структуре.
Гранецентрированная кубическая система тесно связана с гексагональной плотноупакованной (ГПУ) системой, где две системы различаются только относительным расположением своих гексагональных слоев. плоскость гранецентрированной кубической системы является шестиугольной сеткой.
Попытка создать C-центрированную кубическую кристаллическую систему (т.е. размещение дополнительной точки решетки в центре каждой горизонтальной грани) приведет к простой тетрагональной решетке Браве .
Типы кристаллических решеток
Четырнадцать вариантов строения решетки принято объединять в три основных типа. Они следующие:
- Объемно-центрированная кубическая.
- Гексагональная плотноупакованная.
- Гранецентрированная кубическая.
Кристаллическое строение металлов было изучено только благодаря электронной микроскопии, когда стало возможным получать большие увеличения изображений. А классификацию типов решеток впервые привел французский ученый Браве, по фамилии которого их иногда называют.
Дефекты кристаллического строения металлов
Однако все рассмотренные типы ячеек могут иметь и естественные недостатки, или так называемые дефекты. Это может быть связано с разными причинами: посторонними атомами и примесями в металлах, внешними воздействиями и прочим.
Поэтому существует классификация, отражающая дефекты, которые могут иметь кристаллические решетки. Химия как наука изучает каждый из них с целью выявления причины и способа устранения, чтобы свойства материала не были изменены. Итак, дефекты следующие.
- Точечные. Они бывают трех основных видов: вакансии, примеси или дислоцированные атомы. Приводят к ухудшению магнитных свойств металла, электро- и теплопроводности его.
- Линейные, или дислокационные. Выделяют краевые и винтовые. Ухудшают прочность и качество материала.
- Поверхностные дефекты. Влияют на внешний вид и структуру металлов.
В настоящее время разработаны методики устранения дефектов и получения чистых кристаллов. Однако совсем искоренить их не удается, идеальной кристаллической решетки не существует.
Структура Вира – Фелана
Структура Вира – Фелана
В Структура Вира – Фелана есть Pm3n (223) симметрия.
Он имеет 3 ориентации сложенных тетрадекаэдры с участием пиритоэдрический ячейки в зазорах. Встречается как Кристальная структура в химия где он обычно известен как «Тип I клатрат структура». Газовые гидраты образованные метаном, пропаном и диоксидом углерода при низких температурах имеют структуру, в которой воды молекулы лежат в узлах структуры Вира – Фелана и являются водородная связь вместе, и более крупные молекулы газа захвачены в многогранные клетки.
Значение знаний о кристаллическом строении металлов
Из вышеизложенного материала очевидно, что знания о тонкой структуре и строении позволяют спрогнозировать свойства материала и повлиять на них. И это позволяет делать наука химия
9 класс общеобразовательной школы делает в процессе обучения упор на то, чтобы сформировать у учащихся четкое понятие о важном значении основополагающей логической цепочки: состав — строение — свойства — применение
Сведения о кристаллическом строении металлов очень четко иллюстрирует эту зависимость и позволяет учителю наглядно объяснить и показать детям, насколько важно знать тонкую структуру, чтобы правильно и грамотно использовать все свойства
Периодическая таблица и металлы
В XIX веке благодаря своему блестящему уму и многим годам труда Дмитрий Иванович Менделеев составил таблицу, собрав в нее все известные на то время химические элементы. Каждому из них в таблице отведено определенное положение в соответствии с числом протонов в атомном ядре. Вся таблица делится на 7 периодов (горизонтальные строки) и 8 групп (вертикальные строки). Чем больше период, тем больше радиус атома соответствующего элемента, и тем на более высоких орбиталях расположены его валентные электроны. Наоборот, чем старше группа (движение по таблице слева направо), тем больше валентных электронов находится на последней орбитали и тем меньше радиус атома.
Любой элемент таблицы можно условно отнести либо к металлам, либо к неметаллам. Металлы расположены по левую сторону от диагонали бор (B) – полоний (Po). Если взглянуть на таблицу, то можно сразу понять, что количество металлов в несколько раз превышает число неметаллов.
Читать также: Самодельный вискозиметр для краски
Полиморфизм
Кварц – одна из нескольких кристаллических форм кремнезема SiO 2 . Наиболее важные формы кремнезема включают: α-кварц , β-кварц , тридимит , кристобалит , коэсит и стишовит .
Полиморфизм – это появление нескольких кристаллических форм материала. Он содержится во многих кристаллических материалах, включая полимеры , минералы и металлы . Согласно правилам фазового равновесия Гиббса, эти уникальные кристаллические фазы зависят от интенсивных переменных, таких как давление и температура. Полиморфизм связан с аллотропией , которая относится к элементарным твердым телам . Полная морфология материала описывается полиморфизмом и другими переменными, такими как габитус кристаллов , аморфная фракция или кристаллографические дефекты . Полиморфы обладают разной стабильностью и могут спонтанно и необратимо превращаться из метастабильной формы (или термодинамически нестабильной формы) в стабильную форму при определенной температуре. Они также имеют разные температуры плавления , растворимость и дифрактограммы рентгеновских лучей .
Хорошим примером этого является кварцевая форма диоксида кремния или SiO 2 . В подавляющем большинстве силикатов атом Si имеет тетраэдрическую координацию по 4 атомам кислорода. Все кристаллические формы, кроме одной, включают тетраэдрические звенья {SiO 4 }, связанные вместе общими вершинами в разном расположении. В разных минералах тетраэдры демонстрируют разную степень сетки и полимеризации. Например, они встречаются поодиночке, соединены вместе попарно, в более крупные конечные кластеры, включая кольца, цепочки, двойные цепи, листы и трехмерные каркасы. Минералы классифицируются на группы на основе этих структур. В каждой из 7 термодинамически стабильных кристаллических форм или полиморфов кристаллического кварца только 2 из 4 ребер тетраэдров {SiO 4 } являются общими с другими, что дает чистую химическую формулу кремнезема: SiO 2 .
Другой пример – элементарное олово (Sn), которое является пластичным при температурах окружающей среды, но хрупким при охлаждении. Это изменение механических свойств связано с существованием двух его основных аллотропов , α- и β-олова. Два аллотропа , встречающиеся при нормальном давлении и температуре, α-олово и β-олово, более известны как серое олово
и
белое олово
соответственно. Еще два аллотропа, γ и σ, существуют при температурах выше 161 ° C и давлениях выше нескольких ГПа. Белое олово является металлическим и представляет собой стабильную кристаллическую форму при комнатной температуре или выше. При температуре ниже 13,2 ° C олово существует в серой форме, имеющей кубическую кристаллическую структуру алмаза , подобную алмазу , кремнию или германию . Серое олово вообще не имеет металлических свойств, представляет собой тускло-серый порошкообразный материал и имеет несколько применений, кроме нескольких специализированных полупроводниковых применений. Хотя температура α – β превращения олова номинально составляет 13,2 ° C, примеси (например, Al, Zn и т. Д.) Понижают температуру перехода значительно ниже 0 ° C, и при добавлении Sb или Bi превращение может вообще не происходить.
Кристаллографическое использование
В кристаллической структуре геометрическая модель атома является геометрической структурой координации атомов, где определение координации атомов зависит от связей в модели. Например, в каменной соли, ионный состав каждого атома натрия содержит шесть ближайших соседних хлорид-ионов в октаэдрической геометрии и каждый хлорид аналогично — шесть соседних ионов натрия в октаэдрической геометрии. В металлах с объемноцентрированной структурой каждый атом имеет связь с восмью ближайшими другими атомами с кубической геометрией. В металлах с гранецентрированной кубической структурой каждый атом имеет двенадцать связей с соседними атомами с кубооктаэдрической геометрией.
Таблица координационной геометрии
| Координационное число | Геометрия | Изображение | Примеры дискретных (конечных) комплексов | Примеры на кристаллах |
| 2 | линейная | Ag(CN)2− в KAg(CN)2 | Ag в цианиде серебра,Au в AuI | |
| 3 | плоский треугольник | Cu(CN)32− в Na2Cu(CN)3·3H2O | O в TiO2 (структура рутила) | |
| 4 | тетраэдр | CoCl42− | Zn и S в сульфиде цинка, Si в диоксиде кремния | |
| 4 | квадрат | AgF4− | CuO | |
| 5 | тригональная бипирамидальная | SnCl5− | ||
| 5 | квадратная пирамидальная | InCl52− в (NEt4)2InCl5 | ||
| 6 | октаэдр | Fe(H2O)62+ | Na и Cl в хлориде натрия | |
| 6 | тригональная призматическая | Mo(SCHCHS)3 | As в NiAs, Mo в MoS2 | |
| 7 | пентагональная бипирамидальная | ZrF73− в (NH4)3ZrF7 | Pa в PaCl5 | |
| 7 | гранецентрированная октаэдрическая | [HoIII(PhCOCHCOPh)3(H2O)] | La в La2O3 | |
| 7 | тригональная призматическая, квадратическая моногранецентрированная | TaF72− в K2TaF7 | ||
| 8 | куб | Хлорид цезия, фторид кальция | ||
| 8 | квадратная антипризматическая | TaF83− в Na3TaF8 | Хлорид тория(IV) | |
| 8 | Mo(CN)84− в K4[Mo(CN)8].2H2O | Zr в K2ZrF6 | ||
| 8 | гексагональная бипирамидальная | N в Li3N | ||
| 8 | октаэдр | Ni в арсениде никеля | ||
| 8 | Ca в CaFe2O4 | |||
| 8 | тригональная призматическая, квадратная лицевая двуребристая | PuBr3 | ||
| 9 | тригональная призматическая, квадратная лицевая триребристая | [ReH9]2− в нонагидроренате калия | SrCl2·6H2O , Th в RbTh3F13 | |
| 9 | англ. monocapped square antiprismatic | [Th(торополонат)4(H2O)] | La в LaTe2 | |
| 10 | англ. bicapped square antiprismatic | Th(C2O4)42− | ||
| 11 | Th в [ThIV(NO3)4(H2O)3] (NO3−) | |||
| 12 | икосаэдр | Th в Th(NO3)62−-ион в Mg[Th(NO3)6]·8H2O | ||
| 12 | кубооктаэдрон | ZrIV(η³−(BH4)4) | ||
| 12 | ||||
| 14 | двуребристая антипризматичная гексагональная | U(BH4)4 |
Где нет дискретных комплексов означает, что соединения найдены как отдельные единицы сфер вокруг атомов в кристаллах
использованная литература
- ^ абc
П. М. де Вольф, Н. В. Белов, Э. Ф. Берто, М. Дж. Бюргер, Дж. Д. Х. Донней, В. Фишер, Т. Хан, В. А. Копцик, А. Л. Маккей, Х. Вондрачек, А. Дж. К. Уилсон и С. К. Абрахамс (1985). «Номенклатура семейств кристаллов, типов решетки Браве и арифметических классов. Отчет Специального комитета Международного союза кристаллографии по номенклатуре симметрии».
Acta Crystallographica Раздел A
.
41
(3): 278. Дои:10.1107 / S0108767385000587.CS1 maint: несколько имен: список авторов (ссылка на сайт) - Князь, Э., изд. (2006). Международные таблицы для кристаллографии
. Международный союз кристаллографии. Дои:10.1107/97809553602060000001. ISBN 978-1-4020-4969-9 . - Кристаллография и минералы, упорядоченные по кристаллической форме
, Webmineral - Гринвуд, Норман Н.; Эрншоу, Алан (1997). Химия элементов
(2-е изд.). Баттерворт-Хайнеманн. ISBN 978-0-08-037941-8 . - Первоначальное открытие было сделано в J. Chem. Phys. 14
, 569 (1946). - Структура CsCl (B2) В архиве 2008-09-15 на Wayback Machine
- ^ аб
Зейтц,
Современная теория твердого тела
(1940), стр.49 - Структура NaCl (B1) В архиве 2008-10-19 на Wayback Machine
- Sundquist, J. J .; Лин, К. С. (1981). «Электронная структура F-центра в кристалле фторида натрия». Журнал физики C: Физика твердого тела
.
14
(32): 4797–4805. Bibcode:1981JPhC … 14.4797S. Дои:10.1088/0022-3719/14/32/016. - Abrahams, S.C .; Бернштейн, Дж. Л. (1965). «Точность автоматического дифрактометра. Измерение структурных факторов хлорида натрия». Acta Crystallogr.18
(5): 926–932. Дои:10.1107 / S0365110X65002244. - Kao, W .; Перетти, Э. (1970). «Тройная подсистема Sn4As3-SnAs-SnTe». Журнал менее распространенных металлов
.
22
: 39–50. Дои:10.1016/0022-5088(70)90174-8. - ^ абc
J. Aigueperse, P. Mollard, D. Devilliers, M. Chemla, R. Faron, R. Romano, JP Cuer, «Соединения фтора, неорганические» (раздел 4) в Энциклопедии промышленной химии Ульмана, Wiley-VCH, Weinheim, 2005 г. Дои:10.1002 / 14356007.a11_307. - Гу, Чжэн; Эдгар, Дж. Н; Помрой, Дж; Кубалл, М; Коффи, Д. В. (август 2004 г.). «Рост кристаллов и свойства нитрида скандия». Журнал материаловедения: материалы в электронике
.
15
(8): 555–559. Дои:10.1023 / B: JMSE.0000032591.54107.2c. S2CID 98462001. - «Флюорит». aflow.org
. Получено 2020-05-22. - «Каменная соль». aflow.org
. Получено 2020-05-22. - Л. Канторович (2004). Квантовая теория твердого тела.
. Springer. п. 32. ISBN 1-4020-2153-4 . - Биркбек-колледж, Лондонский университет
- Структура цинковой обманки (B3) В архиве 19 октября 2008 г. Wayback Machine
Атомная координация
Рассматривая расположение атомов относительно друг друга, их координационные числа (или количество ближайших соседей), межатомные расстояния, типы связи и т. Д., Можно сформировать общее представление о структурах и альтернативных способах их визуализации.
Тесная упаковка
Решетка ГПУ (слева) и решетка ГЦК (справа)
Используемые принципы можно понять, рассмотрев наиболее эффективный способ упаковки сфер одинакового размера и укладки плотно упакованных атомных плоскостей в трех измерениях. Например, если плоскость A лежит ниже плоскости B, есть два возможных способа размещения дополнительного атома поверх слоя B. Если дополнительный слой был помещен непосредственно над плоскостью A, это привело бы к следующей серии:
…
АБАБАБАБ
…
Такое расположение атомов в кристаллической структуре известно как гексагональная плотная упаковка (ГПУ)
.
Если, однако, все три плоскости расположены в шахматном порядке относительно друг друга и последовательность повторяется только после того, как четвертый слой будет расположен непосредственно над плоскостью A, тогда возникает следующая последовательность:
…
ABCABCABC
…
Этот тип структурного устройства известен как кубическая плотная упаковка (ccp)
.
Элементарной ячейкой ccp-расположения атомов является гранецентрированная кубическая (ГЦК) элементарная ячейка. Это не сразу очевидно, поскольку плотно упакованные слои параллельны плоскостям {111} элементарной ГЦК-ячейки. Есть четыре различных ориентации плотноупакованных слоев.
Эффективность упаковки
может быть разработана путем расчета общего объема сфер и деления на объеме ячейки следующим образом :
4×43πр3162р3знак равноπ32знак равно0,7405 …{\ displaystyle {\ frac {4 \ times {\ frac {4} {3}} \ pi r ^ {3}} {16 {\ sqrt {2}} r ^ {3}}} = {\ frac {\ pi} {3 {\ sqrt {2}}}} = 0,7405 …}
Эффективность упаковки 74% – это максимальная плотность, возможная для элементарных ячеек, построенных из сфер только одного размера. Большинство кристаллических форм металлических элементов – это ГПУ, ГЦК или ОЦК (объемно-центрированная кубическая). Координационное число атомов в ГПУ и ГЦК структуры 12 и ее атомный фактор упаковки (ПФ) это число упоминалось выше, 0,74. Это можно сравнить с APF ОЦК-структуры, равным 0,68.
Многоэлементные соединения
Соединения, состоящие из более чем одного элемента (например, бинарные соединения) часто имеют кристаллические структуры, основанные на кубической кристаллической системе. Здесь перечислены некоторые из наиболее распространенных.
Структура хлорида цезия
А хлорид цезия ячейка. Два цвета сфер представляют два типа атомов.
В космическая группа из хлорид цезия (CsCl) структура называется Pm3м (в Обозначения Германа – Могена) или «221» (в Международных таблицах для кристаллографии). В Strukturbericht обозначение это «B2».[6]
Одна структура — это «взаимопроникающая примитивная кубическая» структура, также называемая структурой «хлорид цезия». Каждый из двух типов атомов образует отдельную примитивную кубическую решетку с атомом одного типа в центре каждого куба другого типа. В элементарной ячейке CsCl каждый ион находится в центре куба ионов противоположного типа, поэтому координационное число равно восьми. В целом расположение атомов такое же, как у объемно-центрированной кубической, но с чередующимися типами атомов в разных узлах решетки. С другой стороны, эту решетку можно было бы рассматривать как простую кубическую структуру с вторичным атомом в кубической пустоте.
Помимо самого хлорида цезия, структура также появляется у некоторых других галогениды щелочных металлов при приготовлении при низких температурах или высоком давлении.[7] Как правило, эта структура с большей вероятностью будет образована из двух элементов, ионы которых имеют примерно одинаковый размер (например, ионный радиус Cs+ = 167 пм, а Cl− = 181 вечера).
В координационный номер каждого атома в структуре — 8: центральный катион координирован с 8 анионами в углах куба, как показано, и аналогично, центральный анион координирован с 8 катионами на углах куба.
Другие соединения, имеющие структуру, подобную хлориду цезия: CsBr, CsI, высокая температура RbCl, AlCo, AgZn, BeCu, MgCe, RuAl и SrTl.[нужна цитата
]
Структура каменной соли
Кристаллическая структура каменной соли. У каждого атома есть шесть ближайших соседей, причем октаэдрическая геометрия.
В космическая группа структуры каменной соли (NaCl) называется Fm3м (в Обозначения Германа – Могена) или «225» (в Международных таблицах для кристаллографии). В Strukturbericht обозначение это «B1».[8]
В каменной соли или хлорид натрия (галит), каждый из двух типов атомов образует отдельную гранецентрированную кубическую решетку, причем две решетки пересекаются друг с другом, образуя трехмерный узор в виде шахматной доски. С другой стороны, можно было бы рассматривать эту структуру как гранецентрированную кубическую структуру с вторичными атомами в ее октаэдрических отверстиях.
Примеры соединений с такой структурой включают сам хлорид натрия, наряду с почти всеми другими галогенидами щелочных металлов, и «многие оксиды, сульфиды, селениды и теллуриды двухвалентных металлов».[7] В более общем смысле, эта структура с большей вероятностью будет сформирована, если катион несколько меньше, чем анион (отношение радиусов катион / анион от 0,414 до 0,732).
Координационное число каждого атома в этой структуре равно 6: каждый катион координирован с 6 анионами в вершинах октаэдр, и аналогично каждый анион координирован с 6 катионами в вершинах октаэдра.
Межатомное расстояние (расстояние между катионом и анионом, или половина длины элементарной ячейки а
) в некоторых кристаллах со структурой каменной соли: 2.3 Å (2.3 × 10−10 м) для NaF,[9] 2,8 Å для NaCl,[10] и 3,2 Å для SnTe.[11]
Другими соединениями, имеющими структуру, подобную каменной соли, являются LiF,[12] LiCl, LiBr, LiI, NaF,[12] NaBr, NaI, KF,[12] KCl, KBr, KI, RbF, RbCl, RbBr, RbI, CsF, MgO, PbS, AgF, AgCl, AgBr[нужна цитата
] и ScN.[13]
В структура флюорита и антифлюоритовые структуры (AB2) также Fm3m структур, но имеют соотношение ионов 1: 2. Они обозначены Вайкофф позиции 4a и 8c, тогда как позиции структуры каменной соли — 4a и 4b.[14][15]
Структура цинковой обманки
Элементарная ячейка из цинковой обманки
В космическая группа структуры цинковой обманки называется F43 м (дюйм Обозначения Германа – Могена) или 216.[16][17] Обозначение Strukturbericht — «B3».[18]
Структура цинковой обманки (также называемая «цинковая обманка») названа в честь минеральной цинковой обманки (сфалерит), одна из форм сульфид цинка (β-ZnS). Как и в структуре каменной соли, два типа атомов образуют две взаимопроникающие гранецентрированные кубические решетки. Однако он отличается от структуры каменной соли тем, как две решетки расположены относительно друг друга. Структура цинковой обманки имеет четырехгранный координация: Ближайшие соседи каждого атома состоят из четырех атомов противоположного типа, расположенных как четыре вершины правильный тетраэдр. В целом расположение атомов в структуре цинковой обманки такое же, как алмаз кубический структура, но с чередующимися типами атомов в разных узлах решетки.
Примеры соединений с такой структурой включают саму цинковую обманку, нитрат свинца (II), многие сложные полупроводники (такие как арсенид галлия и теллурид кадмия) и множество других бинарных соединений.
Другими соединениями, демонстрирующими структуру, подобную цинковой обманке, являются α-AgI, β-BN, алмаз, CuBr, β-CdS, БП и БА.[нужна цитата
]
Наличие порядка в расположении частиц
В аморфном веществе, в отличие от кристаллического, отсутствует какой-либо порядок в расположении частиц. Если же в кристаллическом веществе мысленно соединить прямой два близкоросположенных друг к другу атома, то можно обнаружить, что на этой линии на строго определенных промежутках будут лежать одни и те же частицы:
Таким образом, в случае кристаллических веществах можно говорить о таком понятии, как кристаллическая решетка.
Кристаллической решеткой называют пространственный каркас, соединяющий точки пространства, в которых находятся частицы, образующие кристалл.
Точки пространства, в которых находятся образующие кристалл частицы, называют узлами кристаллической решетки.
В зависимости от того, какие частицы находятся в узлах кристаллической решетки, различают: молекулярную, атомную, ионную и металлическую кристаллические решетки.
В узлах молекулярной кристаллической решетки Кристаллическая решетка льда Кристаллическая решетка льда как пример молекулярной решетки
находятся молекулы, внутри которых атомы связаны прочными ковалентными связями, однако сами молекулы удерживаются друг возле друга слабыми межмолекулярными силами. Вследствие таких слабых межмолекулярных взаимодействий кристаллы с молекулярной решеткой являются непрочными. Такие вещества от веществ с иными типами строения отличаются существенно более низкими температурами плавления и кипения, не проводят электрический ток, могут как растворяться, так и не растворяться в различных растворителях.
Растворы таких соединений могут как проводить, так и не проводить электрический ток в зависимости от класса соединения. К соединениям с молекулярной кристаллической решеткой относятся многие простые вещества — неметаллы (отвержденные H2, O2, Cl2, ромбическая сера S8, белый фосфор P4), а также многие сложные вещества – водородные соединения неметаллов, кислоты, оксиды неметаллов, большинство органических веществ. Следует отметить, что, если вещество находится в газообразном или жидком состоянии, говорить о молекулярной кристаллической решетке неуместно: корректнее использовать термин — молекулярный тип строения.
кристаллическая решетка алмаза Кристаллическая решетка алмаза как пример атомной решетки В узлах атомной кристаллической решетки
находятся атомы. При этом все узлы такой кристаллической решетки «сшиты» между собой посредством прочных ковалентных связей в единый кристалл. Фактически, такой кристалл является одной гигантской молекулой. Вследствие особенностей строения все вещества с атомной кристаллической решеткой являются твердыми, обладают высокими температурами плавления, химически мало активны, не растворимы ни в воде, ни в органических растворителях, а их расплавы не проводят электрический ток. Следует запомнить, что к веществам с атомным типом строения из простых веществ относятся бор B, углерод C (алмаз и графит), кремний Si, из сложных веществ — диоксид кремния SiO2 (кварц), карбид кремния SiC, нитрид бора BN.
У веществ с ионной кристаллической решеткой в узлах решетки находятся ионы, связанные друг с другом посредством ионных связей.
Поскольку ионные связи достаточно прочны, вещества с ионной решеткой обладают сравнительно высокой твердостью и тугоплавкостью. Чаще всего они растворимы в воде, а их растворы, как и расплавы проводят электрический ток. К веществам с ионным типом кристаллической решетки относятся соли металлов и аммония (NH4+), основания, оксиды металлов. Верным признаком ионного строения вещества является наличие в его составе одновременно атомов типичного металла и неметалла.
Кристаллическая решетка хлорида натрия
Кристаллическая решетка хлорида натрия как пример ионной решетки Однако следует отметить, что в веществах с ионным типом строения нередко можно обнаружить, помимо ионных, также ковалентные полярные связи. Это наблюдается в случае сложных ионов, т.е. состоящих из двух или более химических элементов (SO42-, NH4+, PO43- и т.д.). Внутри таких сложных ионов атомы связаны друг с другом ковалентными связями.
Металлическая кристаллическая решетка
наблюдается в кристаллах свободных металлов, например, натрия Na, железа Fe, магния Mg и т.д. В случае металлической кристаллической решетки, в ее узлах находятся катионы и атомы металлов, между которыми движутся электроны. При этом движущиеся электроны периодически присоединяются к катионам, таким образом нейтрализуя их заряд, а отдельные нейтральные атомы металлов взамен «отпускают» часть своих электронов, превращаясь, в свою очередь, в катионы. Фактически, «свободные» электроны принадлежат не отдельным атомам, а всему кристаллу.
Прогнозирование структуры
Сложность предсказания стабильных кристаллических структур на основе знания только химического состава долгое время была камнем преткновения на пути к полностью вычислительному дизайну материалов. Теперь, благодаря более мощным алгоритмам и высокопроизводительным вычислениям, структуры средней сложности могут быть предсказаны с использованием таких подходов, как эволюционные алгоритмы , случайная выборка или метадинамика.
Кристаллические структуры простых ионных твердых веществ (например, NaCl или поваренная соль) уже давно рационализированы с точки зрения правил Полинга , впервые изложенных в 1929 году Линусом Полингом , которого многие с тех пор называют «отцом химической связи». Полинг также рассмотрел природу межатомных сил в металлах и пришел к выводу, что около половины из пяти d-орбиталей в переходных металлах участвуют в связывании, а оставшиеся несвязывающие d-орбитали ответственны за магнитные свойства. Таким образом, он смог соотнести количество d-орбиталей в образовании связи с длиной связи, а также со многими физическими свойствами вещества. Впоследствии он ввел металлическую орбиталь, дополнительную орбиталь, необходимую для разрешения неограниченного резонанса валентных связей между различными электронными структурами.
В теории резонансных валентных связей факторы, определяющие выбор одной из альтернативных кристаллических структур металла или интерметаллического соединения, вращаются вокруг энергии резонанса связей между межатомными положениями. Ясно, что некоторые режимы резонанса будут давать больший вклад (будут более механически устойчивыми, чем другие), и что, в частности, простое соотношение количества связей к количеству позиций будет исключительным. Результирующий принцип заключается в том, что особая стабильность связана с простейшими соотношениями или «числами облигаций»: 1 ⁄ 2 , 1 ⁄ 3 , 2 ⁄ 3 , 1 ⁄ 4 , 3 ⁄ 4 и т. Д. Выбор структуры и значения осевое отношение (которое определяет относительные длины связей), таким образом , является результатом усилий атома , чтобы использовать его валентность в формировании стабильных связей с простыми дробными числами облигаций.
Постулируя прямую корреляцию между концентрацией электронов и кристаллической структурой в сплавах с бета-фазой, Хьюм-Розери проанализировал тенденции изменения точек плавления, сжимаемости и длин связей в зависимости от номера группы в периодической таблице, чтобы установить систему валентностей переходные элементы в металлическом состоянии. Таким образом, эта обработка подчеркнула увеличение прочности сцепления в зависимости от номера группы. Действие направленных сил было подчеркнуто в одной статье о связи между связующими гибридами и металлическими структурами. Результирующая корреляция между электронными и кристаллическими структурами резюмируется одним параметром, весом d-электронов на гибридизованную металлическую орбиталь. «D-вес» составляет 0,5, 0,7 и 0,9 для структур ГЦК, ГПУ и ОЦК соответственно. Таким образом, становится очевидной связь между d-электронами и кристаллической структурой.
При прогнозировании / моделировании кристаллической структуры обычно применяется периодичность, поскольку система представляется неограниченно большой во всех направлениях. Начиная с триклинной структуры без дополнительных предполагаемых свойств симметрии, систему можно заставить показать некоторые дополнительные свойства симметрии, применив Второй закон Ньютона к частицам в элементарной ячейке и недавно разработанное динамическое уравнение для векторов периодов системы (параметры решетки, включая углы ), даже если система подвергается внешним нагрузкам.
Объем
Объем элементарной ячейки определяется в зависимости от ее геометрической формы. Для кубической сингонии он вычисляется как длина грани (межцентровое расстояние атомов), возведенная в третью степень. Для гексагональной сингонии объем можно определить по формуле, указанной ниже:
где a и c – параметры кристаллической решетки, измеряющиеся в ангстремах.
На практике параметры кристаллической решетки рассчитываются для того чтобы в дальнейшем можно было определить структуру соединения, массу атома (исходя из веса данного объема и числа Авогадро) или его радиус.
Обратные решетки различных кристаллов
Обратные решетки для кубической кристаллической системы следующие.
Простая кубическая решетка
Простая кубическая решетка Браве с кубической примитивной ячейкой стороны имеет в качестве обратной стороны простую кубическую решетку с кубической примитивной ячейкой стороны ( в определении кристаллографа). Поэтому кубическая решетка называется самодуальной, имеющей ту же симметрию в обратном пространстве, что и в реальном пространстве. а{\ displaystyle a}2πа{\ displaystyle \ textstyle {\ frac {2 \ pi} {a}}}1а{\ displaystyle \ textstyle {\ frac {1} {a}}}
Гранецентрированная кубическая (ГЦК) решетка
Обратной решеткой для ГЦК-решетки является объемно-центрированная кубическая (ОЦК) решетка со стороной куба . 4πа{\ displaystyle \ textstyle {\ frac {4 \ pi} {a}}}
Рассмотрим составную элементарную ячейку FCC. Найдите примитивную элементарную ячейку FCC; т.е. элементарная ячейка с одной точкой решетки. Теперь возьмем за начало координат одну из вершин примитивной элементарной ячейки. Приведите базисные векторы реальной решетки. Затем по известным формулам можно вычислить базисные векторы обратной решетки. Эти векторы обратной решетки FCC представляют собой базисные векторы реальной решетки BCC
Обратите внимание, что базисные векторы реальной решетки ОЦК и обратной решетки ГЦК похожи друг на друга по направлению, но не по величине.
Объемно-центрированная кубическая (ОЦК) решетка
Обратной решеткой ОЦК- решетки является ГЦК- решетка со стороной куба . 4πа{\ displaystyle \ textstyle {\ frac {4 \ pi} {a}}}
Можно легко доказать, что только решетки Браве с углом между ними 90 градусов (кубический, тетрагональный, ромбический) имеют векторы , параллельные своим векторам в реальном пространстве. (а1,а2,а3){\ displaystyle \ left (\ mathbf {a} _ {1}, \ mathbf {a} _ {2}, \ mathbf {a} _ {3} \ right)}(б1,б2,б3){\ displaystyle \ left (\ mathbf {b} _ {1}, \ mathbf {b} _ {2}, \ mathbf {b} _ {3} \ right)}
Простая шестиугольная решетка
Обратный к простой гексагональной решетке Бравы с решеткой константой с и другим простым гексагональной решеткой с постоянными решетками и повернута на 30 ° вокруг оси с относительно прямой решетки. Поэтому простая гексагональная решетка называется самодуальной, имеющей ту же симметрию в обратном пространстве, что и в реальном пространстве. векторы a 1 = (a (3) 1/2 / 2) i + (a / 2) j; a 2 = – (a (3) 1/2 / 2) i + (a / 2) j ve a 3 = ak 2πc{\ displaystyle \ textstyle {\ frac {2 \ pi} {c}}}4πа3{\ displaystyle \ textstyle {\ frac {4 \ pi} {a {\ sqrt {3}}}}}
Кристалл классы
В изометрическая кристаллическая система
имена классов, точечные группы (в Обозначение Шенфлиса, Обозначения Германа – Могена, орбифолд, и Обозначение Кокстера), тип, примеры, Международные таблицы кристаллографии номер пространственной группы,[2] и космические группы перечислены в таблице ниже. Всего существует 36 кубических пространственных групп.
| # | Группа точек | Тип | пример | Космические группы | ||||||
| имя[3] | Schön. | Intl | Сфера. | Кокс. | Примитивный | По центру лица | По центру тела | |||
| 195–197 | Тетартоидный | 23 | 332 | [3,3]+ | энантиоморфный | Ульманнит, Хлорат натрия | P23 | F23 | I23 | |
| 198–199 | P213 | I213 | ||||||||
| 200–204 | Диплоидный | Тчас | 2 / м3 (м3) | 3*2 | [3+,4] | центросимметричный | Пирит | Вечера3, Pn3 | FM3, Fd3 | я3 |
| 205–206 | Па3 | Я3 | ||||||||
| 207–211 | Гироидальный | 432 | 432 | [3,4]+ | энантиоморфный | Petzite | P432, P4232 | F432, F4132 | I432 | |
| 212–214 | P4332, P4132 | I4132 | ||||||||
| 215–217 | Шестигранный | Тd | 43м | *332 | [3,3] | Сфалерит | п43м | F43м | я43м | |
| 218–220 | п43n | F43c | я43D | |||||||
| 221–230 | Гексоктаэдрический | Очас | 4 / м32 / м (м3м) | *432 | [3,4] | центросимметричный | Галенит, Галит | Вечера3м, Пн3п, Вечера3п, Pn3м | FM3м, Fm3c, Fd3м, Fd3c | Я3м, я3d |
Другие термины для гексоктаэдра: нормальный класс, голоэдральный, дитессераль центральный класс, галенит тип.
Общее понятие о металлах
«Химия. 9 класс» — это учебник, по которому проходят обучение школьники. Именно в нем подробно изучаются металлы. Рассмотрению их физических и химических свойств отведена большая глава, ведь разнообразие их чрезвычайно велико.
Именно с этого возраста рекомендуют давать детям представление о данных атомах и их свойствах, ведь подростки уже вполне могут оценить значение подобных знаний. Они прекрасно видят, что окружающее их разнообразие предметов, машин и прочих вещей имеет в своей основе как раз металлическую природу.
Что же такое металл? С точки зрения химии, к данным атомам принято относить те, что имеют:
- малое число электронов на внешнем уровне;
- проявляют сильные восстановительные свойства;
- имеют большой атомный радиус;
- как простые вещества обладают рядом специфических физических свойств.
Основу знаний об этих веществах можно получить, если рассмотреть атомно-кристаллическое строение металлов. Именно оно объясняет все особенности и свойства данных соединений.
В периодической системе для металлов отводится большая часть всей таблицы, ведь они образуют все побочные подгруппы и главные с первой по третью группу. Поэтому их численное превосходство очевидно. Самыми распространенными являются:
Все металлы имеют ряд свойств, которые позволяют объединять их в одну большую группу веществ. В свою очередь, эти свойства объясняет именно кристаллическое строение металлов.
Объемно-центрированная решетка
Строение кристаллической решетки металлов данного типа представляет собой следующую структуру. Это куб, в узлах которого находится восемь атомов. Еще один располагается в центре свободного внутреннего пространства ячейки, что и объясняет название “объемно-центрированная”.
Это один из вариантов наиболее простого строения элементарной ячейки, а значит, и всей решетки в целом. Такой тип имеют следующие металлы:
- молибден;
- ванадий;
- хром;
- марганец;
- альфа-железо;
- бетта-железо и другие.
Основные свойства таких представителей – высокая степень ковкости и пластичности, твердость и прочность.
Примитивная ячейка
Элементарная ячейка называется примитивной, если ее частицы находятся только в вершинах решетки и отсутствуют в других местах. Ее объем является минимальным по сравнению с другими типами. На практике она оказывается часто низкосимметричной (примером может служить ячейка Вигнера-Зейтца).
У не примитивных ячеек атом в центре объема делит их на 2 или на 4 одинаковые части. В гранецентрированной структуре происходит разделение на 8 частей. В металлографии пользуются понятием элементарной, а не примитивной ячейки, так как симметрия первой позволяет более полноценно описать кристаллическую структуру материала.
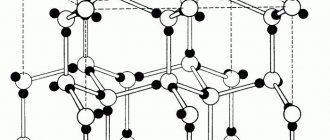
Пустоты в элементарной ячейке
Визуализация кубической элементарной ячейки алмаза: 1. Компоненты элементарной ячейки, 2. Одна элементарная ячейка, 3. Решетка из 3 x 3 x 3 элементарных ячеек.
Простая кубическая элементарная ячейка имеет одну кубическую пустоту в центре.
Объемно-центрированная кубическая элементарная ячейка имеет шесть октаэдрических пустот, расположенных в центре каждой грани элементарной ячейки, и двенадцать дополнительных, расположенных в середине каждого края той же ячейки, в общей сложности шесть октаэдрических пустот. Кроме того, есть 24 тетраэдрических пустоты, расположенных на квадратном расстоянии вокруг каждой октаэдрической пустоты, в общей сложности двенадцать чистых тетраэдрических пустот. Эти тетраэдрические пустоты не являются локальными максимумами и технически не являются пустотами, но иногда они появляются в многоатомных элементарных ячейках.
Гранецентрированная кубическая элементарная ячейка имеет восемь тетраэдрических пустот, расположенных на полпути между каждым углом и центром элементарной ячейки, всего восемь чистых тетраэдрических пустот. Вдобавок есть двенадцать октаэдрических пустот, расположенных в средних точках краев элементарной ячейки, а также одно октаэдрическое отверстие в самом центре ячейки, всего четыре чистых октаэдрических пустот.
Одной из важных характеристик кристаллической структуры является фактор упаковки атомов . Это рассчитывается исходя из предположения, что все атомы являются идентичными сферами, с радиусом, достаточно большим, чтобы каждая сфера упиралась в следующую. Фактор атомной упаковки – это доля пространства, заполненного этими сферами.
Предполагая , один атом за решетку точки, в примитивной кубической решетке с длиной стороны кубы а
, радиус шара будет 2 и атомный фактор упаковки оказывается около 0,524 (что является довольно низким). Точно так же в
ОЦК
решетке фактор упаковки атомов составляет 0,680, а в
ГЦК
– 0,740. Значение
ГЦК
является наивысшим теоретически возможным значением для любой решетки, хотя есть и другие решетки, которые также достигают того же значения, например гексагональная плотноупакованная (
ГПУ
) и одна версия тетраэдрической
ОЦК
.
Как правило, поскольку атомы в твердом теле притягиваются друг к другу, более плотно упакованные атомы имеют тенденцию быть более распространенным. (Хотя могут иметь место неплотно упакованные структуры, например, если орбитальная гибридизация требует определенных валентных углов .) Соответственно, примитивная кубическая структура с особенно низким коэффициентом упаковки атомов встречается редко в природе, но встречается в полонии . ОЦК
и
ГЦК
, с их более высокой плотностью, оба довольно широко распространены в природе. Примеры
ОЦК
включают железо , хром , вольфрам и ниобий . Примеры
ГЦК
включают алюминий , медь , золото и серебро .
Структура и геометрия
Кристаллические решетки представляют совокупность кристаллитов. В ближних зернах они взаимно расположены под некоторым углом. Атомы, представляющие собой микроскопические частицы вещества и наименьшие части химических элементов, в кристаллитах размещены в соответствии с ближним и дальним порядком. Первый подразумевает определенный порядок размещения и стабильности ближайших друг к другу микрочастиц, второй – самых отдаленных. Возможно покидание отдельными атомами мест расположения вследствие диффузии, однако это не приводит к нарушению упорядоченности строения.
Тип решетки определяют формой простейшего геометрического тела, образующего ее. Кубические решетки дифференцируют на четыре вида:
- кубическая с микрочастицами в углах;
- объемно-центрированный вариант имеет восемь атомов, расположенных по углам, и один в центре;
- гранецентрированная кубическая решетка отличается размещением атомов в центрах граней и вершинах;
- гексагональная плотноупакованная с нахождением микрочастиц в углах шестигранной призмы, в центре оснований и трех в центральной плоскости.
К основным параметрам решеток относят компактность, под которой понимают степень заполнения объема атомами. Ее определяют тремя прочими показателями:
- параметр решетки – значение межатомного расстояния в нм по ребру простейшей ячейки (характеризуется для кубических вариантов длиной ребра);
- координационное число, под которым понимают количество ближайших соседних микрочастиц;
- плотность упаковки, представленная отношением общего атомного объема решетки и ее общего объема.
Для измерения параметра решеток применяют рентгеноструктурный метод анализа. При подсчете количества атомов учитывают, что каждый из них принадлежит к нескольким ячейкам сразу. Для кубических решеток исключение представляет размещенная в центре куба микрочастица.
Для объемно-центрированного типа координационное число составляет 8 по числу ближайших атомов к центральному. Для гранецентрированного варианта микрочастица на кубической грани размещена на одинаковом расстоянии от четырех в углах, четырех на гранях, четырех ближайшей кристаллической ячейки. То есть, координационное число составляет 12.
Различные варианты кристаллических решеток характеризуются разной плотностью упаковки. Для простой кубической решетки координационное число равно 6, для ОЦК — 8, ГЦК и ГП (гексагональной плотноупакованной) — 12.
Для объемно-центрированного варианта объемы микрочастиц и межатомных промежутков соотносятся в пропорции 68/32%, для ГЦК значения соответствующих параметров равны 74 и 26% соответственно. Компактность решетки определяется особенностями металлической электронной структуры и характером атомной связи.
Ввиду упорядоченности решетки возможно выделение кристаллографических плоскостей и направлений.
Под направлениями понимают прямые, вдоль которых находятся атомы. То есть они представлены ребрами, диагоналями и гранями.
Плоскости подразделяют на диагональные и плоскости кубических граней.
Для обозначения данных категорий применяют трехзначные индексы. Для направлений их определяют путем нахождения ближайшего атома и использования его координат относительно точки O. Для плоскостей находят координаты точек их пересечения с осями координат и меняют на обратные.
Следует отметить, что в кристаллических телах наблюдается изменение механических свойств вдоль направлений. Данная особенность, называемая анизотропией, объясняется различной атомной плотностью. Так, для кубических решеток вдоль диагоналей и на диагональных плоскостях данный показатель больше, чем вдоль ребер и на проходящих сквозь грани плоскостях. При этом анизотропия наблюдается в пределах кристаллита либо монокристалла. Для поликристаллических тел она нехарактерна ввиду усреднения параметров по всем направлениям для большого числа произвольно взаимно ориентированных зерен. Ввиду этого металлы относят к псевдо- или квазиизотропным телам.
Кроме того, для некоторых металлов (Ti, Fe, Sn) характерна аллотропия, под которой понимают изменение кристаллического строения путем изменения типа простейшей ячейки. Также данное свойство называют полиморфизмом.
Так, у железа в температурном интервале 911-1392 °C кубическая решетка гранецентрированного типа, а при температурах за пределами приведенного диапазона – отдельно-центрированная (до плавления при 1539 °C). Для дифференциации аллотропических форм применяют греческие буквы.
Возможно наличие дефектов решетки. Их классифицируют на несколько типов.
- Точечные, по размеру близкие к атомам, представлены вакансиями (пустые узлы, межузельные микрочастицы), примесными атомами замещения (того же размера, что и исходные) и внедрения (маленькие микрочастицы в междоузлиях).
- Линейные (протяженные) представлены дислокациями (плоскостные смещения). Их классифицируют на наиболее распространенные краевые (экстраплоскость или полуплоскость) и винтовые (закручивание плоскостей).
- Поверхностные – искажения на границах зерен ввиду передвигающихся зерен дислокации.
- Объемные – поры и трещины.
Названные дефекты по-разному сказываются на прочности. Для точечных степень влияния на данный показатель определяется их характером и числом в конкретном объеме. Линейные дефекты ввиду большой подвижности значительно сказываются на прочности, упрощая сдвиги кристаллитов под влиянием напряжений. Воздействие линейных дефектов на прочность оценивают по их плотности (отношение их общей длины к объему материала). Ее предельное значение – 1013 см-2 (при большем происходит разрушение). На основе того, что мелкозернистые материалы более прочны в сравнении с крупнозернистыми при большей общей протяженности границ, поверхностные дефекты наоборот повышают прочность. Объемные, помимо непосредственного снижения прочности, значительно повышают напряжения от рабочих нагрузок, концентрируя их.
Дефекты кристаллического строения металлов
Однако все рассмотренные типы ячеек могут иметь и естественные недостатки, или так называемые дефекты. Это может быть связано с разными причинами: посторонними атомами и примесями в металлах, внешними воздействиями и прочим.
Поэтому существует классификация, отражающая дефекты, которые могут иметь кристаллические решетки. Химия как наука изучает каждый из них с целью выявления причины и способа устранения, чтобы свойства материала не были изменены. Итак, дефекты следующие.
- Точечные. Они бывают трех основных видов: вакансии, примеси или дислоцированные атомы. Приводят к ухудшению магнитных свойств металла, электро- и теплопроводности его.
- Линейные, или дислокационные. Выделяют краевые и винтовые. Ухудшают прочность и качество материала.
- Поверхностные дефекты. Влияют на внешний вид и структуру металлов.
В настоящее время разработаны методики устранения дефектов и получения чистых кристаллов. Однако совсем искоренить их не удается, идеальной кристаллической решетки не существует.
Свойства металлов
К специфическим свойствам рассматриваемых веществ относят следующие.
- Металлический блеск. Все представители простых веществ им обладают, причем большинство одинаковым серебристо-белым цветом. Лишь некоторые (золото, медь, сплавы) отличаются.
- Ковкость и пластичность — способность деформироваться и восстанавливаться достаточно легко. У разных представителей выражена в неодинаковой мере.
- Электропроводность и теплопроводность — одно из основных свойств, которое определяет области применения металла и его сплавов.
Кристаллическое строение металлов и сплавов объясняет причину каждого из обозначенных свойств и говорит о выраженности их у каждого конкретного представителя. Если знать особенности такого строения, то можно влиять на свойства образца и подстраивать его под нужные параметры, что и делают люди уже многие десятилетия.