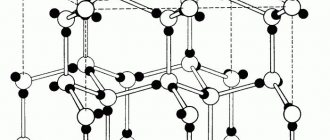
Crystal lattices
The crystal lattice is the spatial arrangement of atoms or ions in a crystal.
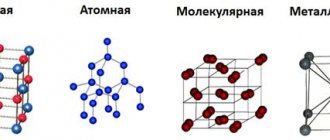
The points of the crystal lattice at which atoms or ions are located are called lattice nodes. Crystal lattices are divided into molecular, atomic, ionic and metallic.
It is very important not to confuse the type of chemical bond and crystal lattice. Remember that crystal lattices reflect the spatial arrangement of atoms.
Molecular crystal lattice
Molecules are located at the nodes of a molecular lattice. Under normal conditions, most gases and liquids have a molecular lattice. Bonds are most often covalent polar or nonpolar.
The classic example of a substance with a molecular lattice is water, so associate the properties of these substances with water. Substances with a molecular lattice are fragile, have low hardness, are volatile, fusible, capable of sublimation, and are characterized by low boiling points.
Examples: NH3, H2O, Cl2, CO2, N2, Br2, H2, I2. I would especially like to mention white phosphorus, orthorhombic, plastic and monoclinic sulfur, and fullerene. We studied these allotropic modifications in detail in an article devoted to the classification of substances.
Ionic crystal lattice
At the sites of the ionic lattice there are atoms connected by ionic bonds. This type of lattice is characteristic of substances that have ionic bonds: metal salts, oxides and hydroxides.
Metal crystal lattice
The nodes of the metal lattice contain metal atoms. This type of lattice is characteristic of substances formed by a metallic bond.
Associate the properties of these substances with copper. They have a characteristic metallic luster, are malleable and ductile, conduct electricity and heat well, and have high melting and boiling points.
Examples: Cu, Fe, Zn, Al, Cr, Mn.
Atomic crystal lattice
At the sites of the atomic lattice there are atoms connected by covalent polar or nonpolar bonds.
Associate these substances with sand. They are very hard, very refractory (high melting point), non-volatile, durable, and insoluble in water.
Examples: SiO2, B, Ge, SiC, Al2O3. I would especially like to highlight: diamond and graphite (C), red and black phosphorus (P).
© Bellevich Yuri Sergeevich 2018-2021
This article was written by Yuri Sergeevich Bellevich and is his intellectual property. Copying, distribution (including by copying to other sites and resources on the Internet) or any other use of information and objects without the prior consent of the copyright holder is punishable by law. To obtain article materials and permission to use them, please contact Yuri Bellevich
.
Source
Molecular kinetic theory
All molecules are made up of tiny particles called atoms. All currently discovered atoms are collected in the periodic table.
An atom is the smallest, chemically indivisible particle of a substance that retains its chemical properties. Atoms are connected to each other by chemical bonds . Previously, we already looked at the types of chemical bonds and their properties. Be sure to study the theory on the topic: Types of chemical bonds before studying this article!
Now let's look at how particles in matter can connect.
Depending on the location of the particles relative to each other, the properties of the substances they form can vary greatly. far from each other (the distance between the particles is much greater than the size of the particles themselves), practically do not interact with each other, and move in space chaotically and continuously, then we are dealing with a gas .
If the particles are located close to each other, but chaotically , interact more with each other , perform intense oscillatory movements in one position, but can jump to another position, then this is a model of the structure of a liquid .
If the particles are located close to each other, but in a more orderly manner , and interact more with each other, and move only within one equilibrium position, practically without moving to other positions, then we are dealing with a solid substance .
Most known chemical substances and mixtures can exist in solid, liquid and gaseous states. The simplest example is water. Under normal conditions it is liquid , at 0 oC it freezes - it goes from a liquid to a solid , and at 100 oC it boils - it goes into the gas phase - water vapor. Moreover, many substances under normal conditions are gases, liquids or solids. For example, air - a mixture of nitrogen and oxygen - is a gas under normal conditions. But at high pressure and low temperature, nitrogen and oxygen condense and pass into the liquid phase. Liquid nitrogen is actively used in industry. Sometimes plasma , as well as liquid crystals, as separate phases.
Many properties of individual substances and mixtures are explained by the relative arrangement of particles in space relative to each other!
This article examines the properties of solids , depending on their structure. Basic physical properties of solids: melting point, electrical conductivity, thermal conductivity, mechanical strength, plasticity, etc.
Melting point is the temperature at which a substance changes from solid to liquid and vice versa.
Plasticity is the ability of a substance to deform without breaking.
Electrical conductivity is the ability of a substance to conduct current.
Current is the ordered movement of charged particles . Thus, only substances that contain mobile charged particles . Based on their ability to conduct current, substances are divided into conductors and dielectrics. Conductors are substances that can conduct current (i.e. contain mobile charged particles). Dielectrics are substances that practically do not conduct current.
In a solid matter, the particles of a substance can be arranged randomly or more ordered . randomly located in space , the substance is called amorphous . Examples of amorphous substances are coal, mica glass.
If the particles of a solid substance are arranged in space in an orderly manner, i.e. form repeating three-dimensional geometric structures, such a substance is called a crystal , and the structure itself is called a crystal lattice . Most of the substances we know are crystals. The particles themselves are located at the nodes of the crystal lattice.
Crystalline substances are distinguished, in particular, by the type of chemical bond between particles in the crystal - atomic, molecular, metallic, ionic; according to the geometric shape of the simplest cell of a crystal lattice - cubic, hexagonal, etc.
Depending on the type of particles that form the crystal lattice, atomic, molecular, ionic and metallic crystal structures are distinguished.
Physical properties of copper:
| 204 | Atomic radius (calculated) | 145 pm |
| 205 | Empirical atomic radius* | 135 pm |
| 206 | Covalent radius* | 132 pm |
| 207 | Ion radius (crystalline) | Cu + (in parentheses the coordination number is indicated - a characteristic that determines the number of nearest particles (ions or atoms) in a molecule or crystal) |
| 208 | Van der Waals radius | 140 pm |
| 209 | Electrons, Protons, Neutrons | 29 electrons, 29 protons, 35 neutrons |
| 210 | Family (block) | d-family element |
| 211 | Period in the periodic table | 4 |
| 212 | Group on the periodic table | 11th group (according to the old classification - a secondary subgroup of the 1st group) |
| 213 | Emission spectrum | |
| 306 | Electron affinity energy of an atom | 119.235(4) kJ/mol (1.23578(4) eV) |
| 400 | Physical properties | |
| 401 | Density* | 8.96 g/cm 3 (at 20 °C and other standard conditions, state of matter - solid), |
8.02 g/cm 3 (at a melting point of 1084.62 °C and other standard conditions, the state of the substance is liquid),
7.962 g/cm 3 (at 1127 °C and other standard conditions, the state of matter is liquid), 7.881 g/cm 3 (at 1227 °C and other standard conditions, the state of matter is liquid), 7.799 g/cm 3 (at 1327 °C and other standard conditions, state of matter - liquid), 7.471 g/cm 3 (at 1727 °C and other standard conditions, state of matter - liquid), 7.307 g/cm 3 (at 1927 °C and other standard conditions, state substances - liquid),
7.225 g/cm 3 (at 2027 °C and other standard conditions, the state of matter is liquid), 7.102 g/cm 3 (at 2177 °C and other standard conditions, the state of matter is liquid)
General information:
| 100 | General information | |
| 101 | Name | Copper |
| 102 | Former name | |
| 103 | Latin name | Cuprum |
| 104 | English name | Copper |
| 105 | Symbol | Cu |
| 106 | Atomic number (number in table) | 29 |
| 107 | Type | Metal |
| 108 | Group | Transitional, heavy, non-ferrous metal |
| 109 | Open | Known since ancient times |
| 110 | Opening year | 9000 BC |
| 111 | Appearance, etc. | Plastic metal of golden-pink color (or pink in the absence of an oxide film) |
| 112 | Origin | Natural material |
| 113 | Modifications | |
| 114 | Allotropic modifications | |
| 115 | Temperature and other conditions for the transition of allotropic modifications into each other | |
| 116 | Bose-Einstein condensate | |
| 117 | 2D materials | |
| 118 | Content in the atmosphere and air (by mass) | 0 % |
| 119 | Content in the earth's crust (by mass) | 0,0068 % |
| 120 | Content in seas and oceans (by mass) | 3,0·10-7 % |
| 121 | Content in the Universe and space (by mass) | 6,0·10-6 % |
| 122 | Abundance in the Sun (by mass) | 0,00007 % |
| 123 | Content in meteorites (by mass) | 0,011 % |
| 124 | Content in the human body (by weight) | 0,0001 % |
Additional information:
| 402 | Melting temperature* | 1084.62 °C (1357.77 K, 1984.32 °F) |
| 403 | Boiling temperature* | 2562 °C (2835 K, 4643 °F) |
| 404 | Sublimation temperature | |
| 405 | Decomposition temperature | |
| 406 | Self-ignition temperature of a gas-air mixture | |
| 407 | Specific heat of fusion (enthalpy of fusion ΔHpl)* | 13.26 kJ/mol |
| 408 | Specific heat of evaporation (enthalpy of boiling ΔHboiling)* | 300.4 kJ/mol |
| 409 | Specific heat capacity at constant pressure | 0.384 J/g K (at 20 °C) |
| 410 | Molar heat capacity | 24.44 J/(K mol) |
| 411 | Molar volume | 7.1 cm³/mol |
| 412 | Thermal conductivity | 401 W/(mK) (at standard conditions), 401 W/(mK) (at 300 K) |
| 413 | Thermal expansion coefficient | 16.5 µm/(MK) (at 25 °C) |
| 414 | Thermal diffusivity coefficient | |
| 415 | Critical temperature | |
| 416 | Critical pressure | |
| 417 | Critical Density | |
| 418 | Triple point | |
| 419 | Vapor pressure (mmHg) | 0.000000001 mmHg (at 672°C), 0.00000001 mmHg. (at 727°C), 0.0000001 mmHg. (at 787°C), 0.000001 mmHg. (at 857°C), 0.00001 mmHg. (at 934°C), 0.0001 mmHg. (at 1025°C), 0.001 mmHg. (at 1133°C), 0.01 mmHg. (at 1264°C), 0.1 mmHg. (at 1419°C), 1 mmHg. (at 1617°C), 10 mmHg. (at 1910°C), 100 mmHg. (at 2312°C) |
| 420 | Vapor pressure (Pa) | 1 Pa (at 1509 K), 100 kPa (at 2834 K) |
| 421 | Standard enthalpy of formation ΔH | 0 kJ/mol (at 298 K, for the state of matter - solid), 338 kJ/mol (at 298 K, for the state of matter - gas) |
| 422 | Standard Gibbs energy of formation ΔG | 0 kJ/mol (at 298 K, for the state of matter - solid) |
| 423 | Standard entropy of matter S | 33.15 J/(mol K) (at 298 K, for the state of matter - solid), 166.3 J/(mol K) (at 298 K, for the state of matter - gas) |
| 424 | Standard molar heat capacity Cp | 24.4 J/(mol K) (at 298 K, for the state of matter - solid), |
Copper crystal lattice:
500
| Crystal cell | ||
| 511 | Crystal grid #1 | |
| 512 | Lattice structure | Cubic face centered |
| 900 | additional information | |
| 901 | CAS number | 7440-50-8 |
Note:
205* The empirical radius of the copper atom according to [1] and [3] is 128 pm.
206* Covalent radius of copper according to [1] and [3] is 132±4 pm and 117 pm, respectively.
401* The density of copper according to [3] is 8.92 g/cm 3 (at 0 °C and under normal conditions, the state of the substance is a solid).
402* The melting point of copper according to [3] and [4] is 1083.4 °C (1356.55 K, 1982.12 °F) and 1083 °C (1356.15 K, 1981.4 °F), respectively.
403* The boiling point of copper according to [3] and [4] is 2567 °C (2840.15 K, 4652.6 °F) and 2543 °C (2816.15 K, 4609.4 °F), respectively.
407* The specific heat of fusion (enthalpy of fusion ΔHmelt) of copper according to [3] and [4] is 13.01 kJ/mol and 13 kJ/mol, respectively.
408* The specific heat of evaporation (enthalpy of boiling ΔHboiling) of copper according to [3] and [4] is 304.6 kJ/mol and 302 kJ/mol, respectively.
Source
Copper crystal lattice
Tell me, what does the crystal lattice of copper look like? Characterize the valence capabilities of the copper atom (you must indicate the electronic formula of copper and the number of unpaired electrons).
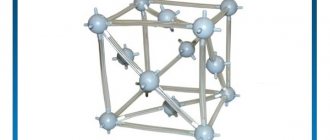
In its simple form, copper is a red metal. The crystal lattice of copper is face-centered cubic. The crystal lattice is a kind of spatial frame formed by intersecting straight lines. At the points of intersection of the lines—lattice nodes—the centers of the particles lie. The crystal lattice of copper is molecular. This means that there are molecules in its nodes. They are connected to each other by intermolecular forces.
Rice. 1. Schematic representation of the copper crystal lattice.
Copper is a metal that belongs to the d-family elements. The electronic configuration of copper is as follows:
.
In copper crystals the metallic type of chemical bond is realized. Metallic is usually called a bond between metal atoms in the solid state. In the gas phase, the usual covalent nonpolar bond takes place between metal atoms. During the formation of a solid, as in any crystals, energy bands are formed - delocalized molecular orbitals. Unlike ionic crystals, the energy bands in metal crystals are much wider and can even overlap, which is due to the high degree of overlap of metal atomic orbitals and their high coordination numbers.
Source
Modern ideas about the structure of matter
Modern science states that an atom consists of a charged nucleus, which carries a positive charge, and electrons, which carry negative charges. At a speed of several thousand trillion revolutions per second, electrons rotate in their orbits, creating an electron cloud around the nucleus. The positive charge of the nucleus is numerically equal to the negative charge of the electrons. Thus, the atom of the substance remains electrically neutral. Possible interactions with other atoms occur when electrons are detached from their parent atom, thereby disturbing the electrical balance. In one case, the atoms are arranged in a certain order, which is called a crystal lattice. In another, due to the complex interaction of nuclei and electrons, they are combined into molecules of various types and complexity.
1.1. Amorphous and crystalline bodies
In solids, atoms can be arranged in space in two ways:
Amorphous substances have the formal characteristics of solids, i.e. they are able to maintain constant volume and shape. However, they do not have a specific melting or crystallization point.
The outer electron orbits of the atoms touch, so the packing density
atoms in the crystal lattice is very large.
In crystallites, short- and long-range orders are observed. This means the presence of an ordered arrangement and stability as its nearest neighbors surrounding a given atom ( short-range order
), and atoms located at significant distances from it, up to the grain boundaries (
long-range order
).
Rice. 1.1. Arrangement of atoms in crystalline (a) and amorphous (b) matter
Due to diffusion
individual atoms can leave their places in the nodes of the crystal lattice, but the order of the crystal structure as a whole is not disrupted.
Grating characteristics
Crystal lattices are characterized by compactness or degree of fullness. Compactness is determined by the following indicators:
- lattice parameter – distance between atoms;
- number of atoms;
- coordination number – the number of neighboring cells;
- Packing density is the ratio of the volume occupied by atoms to the total volume of the lattice.
When counting the number of atoms, it should be remembered that atoms at nodes and faces are part of neighboring cells.
Rice. 3. Crystal cells make up a lattice.
1.2. Main types of crystal lattices
All metals are crystalline bodies that have a certain type of crystal lattice, consisting of low-mobility positively charged ions, between which free electrons move (the so-called electron gas
).
This type of structure is called a metallic bond
.
The type of lattice is determined by the shape of an elementary geometric body, the repeated repetition of which along three spatial axes forms the lattice of a given crystalline body.
body-centered cubic (bcc)
face-centered cubic (fcc)
hexagonal close-packed (HP)
(6 atoms per cell)
Rice. 1.2. Main types of metal crystal lattices
The basis of the bcc lattice is an elementary cubic cell (Fig. 1.2, b), in which positively charged metal ions are located at the vertices of the cube, and another atom in the center of its volume, i.e. at the intersection of its diagonals. Iron, chromium, vanadium, tungsten, molybdenum and other metals have this type of lattice in certain temperature ranges.
In an fcc lattice (Fig. 1.2, c), the unit cell is a cube with centered faces. Iron, aluminum, copper, nickel, lead and other metals have a similar lattice.
The third common type of close-packed lattices is hexagonal close-packed (HCP, Fig. 1.2, d). The GPU cell consists of spaces spaced from each other by a parameter c
parallel centered hexagonal bases. Three ions (atoms) are located on the middle plane between the bases.
For hexagonal lattices, the ratio of the parameter with
/
a
is always greater than one. Magnesium, zinc, cadmium, beryllium, titanium, etc. have such a lattice.
The compactness of the crystal lattice or the degree to which its volume is filled with atoms is an important characteristic. It is determined by such indicators as the lattice parameter, the number of atoms in each unit cell, the coordination number and packing density.
Parameters a
cubic metal lattices range from 0.286 to 0.607 nm.
For metals with a hexagonal lattice, a
lies in the range of 0.228-0.398 nm, and
c
in the range of 0.357-0.652 nm.
The crystal lattice parameters of metals can be measured using X-ray diffraction analysis.
When calculating the number of atoms in each unit cell, it should be kept in mind that each atom is simultaneously included in several cells. For example, for an fcc lattice, each atom located at the vertex of a cube belongs to 8 cells, and the atom centering the face belongs to two. And only the atom located in the center of the cube completely belongs to this cell.
Thus, bcc and fcc cells contain 2 and 4 atoms, respectively.
Under the coordination number
refers to the number of nearest neighbors of a given atom.
Rice. 1.3. Coordination number in various crystal lattices for atom A:
In a bcc lattice (Fig. 1.3, a
) atom
A
(in the center) is at the closest equal distance from the eight atoms located at the vertices of the cube, i.e., the coordination number of this lattice is 8 (K8).
In an fcc lattice (Fig. 1.3, b)
atom
A
(on the face of the cube) is at the closest equal distance from the four atoms /,
2, 3, 4
located at the vertices of the cube, from the four atoms
5, 6, 7, 8
located on the faces of the cube, and, in addition, from four atoms
9, 10, 11, 12,
belonging to a nearby crystal cell.
Atoms 9, 10, 11, 12
are symmetrical to atoms 5,
6, 7, 8.
Thus, the coordination number of the fcc lattice is 12 (K12).
In an HCP lattice with c/a =
1.633 (Fig. 1.3, c) atom
A
in the center of the hexagonal base of the prism is at the closest equal distance from six atoms /,
2, 3, 4, 5, 6,
located at the vertices of the hexagon, and from three atoms
7, 8, 9 ,
located in the middle plane of the prism.
In addition, atom A
is at the same distance from three more atoms
10, 11, 12,
belonging to the crystal cell lying below the base.
Atoms 10, 11, 12
are symmetrical to atoms
7, 8, 9.
Therefore, for the hcp lattice the coordination number is 12 (Г12).
Packing density is the ratio of the total volume occupied by the actual atoms in the crystal lattice to its total volume. Different types of crystal lattices have different atomic packing densities. In an fcc lattice, atoms occupy 74% of the total volume of the crystal lattice, and interatomic spaces (“pores”) occupy 26%. In a bcc lattice, atoms occupy 68% of the total volume, and “pores” occupy 32%. The compactness of the lattice depends on the characteristics of the electronic structure of the metals and the nature of the bonds between their atoms.
The properties of the metal greatly depend on the type of crystal lattice.
General structure
Metals are solid substances with a crystalline structure. The exception is mercury, a liquid metal. Crystal lattices are metal atoms ordered in a certain way. Each atom consists of a positively charged nucleus and several negatively charged electrons. Metal atoms don't have enough electrons, so they are ions.
A unit of a crystal lattice is an elementary crystal cell, in the conventional nodes and on the faces of which there are positively charged ions. They are held together by metallic bonds that arise due to the random movement of electrons separated from the atoms (due to which the atoms turned into ions).
Rice. 1. Metal connection diagram.
The free movement of electrons determines the electrical and thermal conductivity of metals.
1.3. Crystallographic directions and planes
The orderliness of the crystal structure in the spatial lattice makes it possible to distinguish individual crystallographic directions and planes.
Crystallographic planes are, for example, the planes of the faces of cubes (Fig. 1.4, b), as well as their various diagonal planes together with the atoms located on them (Fig. 1.4, c, d). For hcp lattices, the crystallographic planes can be the planes of the bases (Fig. 1.2, d).
To determine the index of any direction, it is necessary to find the index of the atom closest to a given reference point located in a given direction. For example, the index of the nearest atom along the OX
indicated by the numbers 100 (Fig. 1.4,a).
This and the numbers represent the coordinates of the mentioned atom relative to point O, expressed through the number of parameters along the OX, OY
and
OZ
, respectively.
The indices of the direction OX and directions parallel to it are designated [100]. Accordingly directions OY
and
OZ
are designated [010] and [001].
of the XOZ, XOY,
and
YOZ
faces are designated [101], [110], and [011]. Using this technique, you can determine the index of any direction. For example, the direction index along the diagonal of a cube is expressed as follows: [111].
Indices of planes parallel to XOZ
and
YOZ,
the expressions (010) and (100) will appear (Fig. 1.4, b). The index of the vertical diagonal plane of the cube will be expressed through (110), (Fig. 1.2, c), and the index of the inclined plane, intersecting with all three coordinate axes at a distance of one parameter, will take the form (111) (see Fig. 1.4, d).
1.4. Anisotropy in crystals
Under Anisotropy
understands the dissimilarity of mechanical and other properties in crystalline bodies along different crystallographic directions. It is a natural consequence of the crystal structure, since the atomic density is different on different crystallographic planes and along different directions.
For example, in cubic lattices (see Fig. 1.2, b, c) there are fewer atoms in the directions along the edges than along the diagonals of the cube in the bcc lattice or the diagonals of the faces in the fcc lattice. There are fewer atoms on the planes passing through the faces of the bcc and fcc lattices than on the diagonal planes.
Since the mechanical, physical and chemical properties along different directions depend on the density of the atoms located on them, the listed properties along different directions in crystalline solids should not be the same.
Anisotropy appears only within one single crystal or crystallite grain. In polycrystalline solids it is not observed due to the averaging of properties in each direction for a huge number of grains randomly oriented relative to each other. Therefore, real metals are quasi-isotropic bodies, that is, pseudo-isotropic.
Rice. 1.5. Unit cell of a bcc lattice
Shear in a crystal occurs most easily along atomic planes with the densest packing of atoms. Consider a body-centric cubic lattice (BCC) (Fig. 1.5):
Rice. 1.6. BCC lattice planes
Types of gratings
Unit crystal cells can have different configurations. In this regard, three types of crystal lattices are distinguished:
- body-centered (bcc) cubic – consists of 9 ions;
- face-centered (fcc) cubic – includes 14 ions;
- hexagonal close-packed (hcp) - consists of 17 ions.
A bcc is a cube with an atom at its nodes. The ninth ion is located in the center of the cube, at the intersection of the diagonals. This type is typical for iron, molybdenum, chromium, tungsten, and vanadium.
The elementary crystalline cell of the fcc type is a cube with ions at the nodes and in the middle of each face - at the intersection of the diagonals. Copper, silver, aluminum, lead, and nickel have this structure.
The third type has the form of a hexagonal prism, the nodes of which contain six ions on each side. One ion is located in the middle between the six nodes. In the middle of the prism between the hexagonal faces there is an equilateral triangle, which is made up of three ions.
A metal can contain a large number of atomic structure defects. Defects affect the properties of the metal.
1.5. Allotropy of metals
Some metals, for example, iron, titanium, tin, etc., are capable of changing their crystal structure upon reaching certain temperatures, i.e., changing the type of unit cell of their crystal lattice. This phenomenon is called allotropy
or
polymorphism
, and the transitions themselves from one crystalline structure to another are called allotropic or polymorphic.
In Fig. Figure 1.7 shows the change free energy
F
as a function of temperature
t
for two variants of the crystalline structure of iron: bcc (curve
1
) and fcc (curve
2).
In the temperature range 911-1392 o C, iron has an fcc lattice, since in this case its free energy is less. At t 1392°C, it should have a bcc lattice, which has less free energy.
1.6. Metal lattice defects
A crystal lattice in which there are no discontinuities and all nodes are filled with homogeneous atoms is called an ideal crystal lattice of a metal.
The lattice of real metal may contain various defects.
All crystal lattice defects are usually divided into point, linear, surface and volumetric.
Point defects are comparable to the size of atoms. These include vacancies, i.e., unfilled lattice sites, interstitial atoms of a given metal (Figure 1.8), substitutional impurity atoms, i.e., atoms comparable in diameter to the atoms of a given metal and interstitial impurity atoms, which have very small sizes and therefore located in internodes (Figure 1.9). The effect of these defects on the strength of the metal can be different depending on their number per unit volume and nature.
Rice. 1.8. Scheme of formation of a vacancy-interstitial atom pair
Rice. 1.9. Impurity interstitial and substitution atoms
Linear defects have a length that significantly exceeds their transverse dimensions. These include dislocations
, i.e., defects formed in the lattice as a result of displacements of crystallographic planes.
There are two types of dislocations.
The most characteristic is the edge dislocation
(Fig. 1.10). It is formed as a result of the appearance of a so-called half-plane or extra-plane in the lattice.
Rice. 1.10. Scheme of edge dislocation in an ideal crystal
The bottom row of the extraplane is actually called a dislocation.
Another type of dislocation is a screw dislocation
, which represents a certain conventional axis inside the crystal, around which atomic planes are twisted (Fig. 1.11).
Rice. 1.11. Screw dislocation diagram
In a screw dislocation, as well as in an edge dislocation, significant distortions of the crystal lattice are observed only near the axis, therefore such a defect can be classified as linear.
Dislocations have high mobility, therefore they significantly reduce the strength of the metal, since they facilitate the formation of shears in crystallite grains under the influence of applied stresses.
Dislocation mechanism of shear plastic deformation
inside crystals may lead to destruction of the product. Thus, dislocations directly affect the strength characteristics of the metal.
In Fig. 1.12 as an ABC
The dependence of metal strength on dislocation density is schematically shown.
Point A
corresponds to
With an increase in the number of dislocations (see section AB)
the strength decreases sharply, since the forces required to effect shifts in the grains of the metal during its deformation and destruction are reduced by several orders of magnitude.
Rice. 1.12. Dependence of the ultimate strength of a crystal on the density of linear defects (dislocations). Odinga curve
At a dislocation density of 10 6-10 7 cm-2 (point B
on the curve), strength is minimal, and in the
BC
it increases. This is explained by the fact that as the density of dislocations increases, their movement occurs not only along parallel, but also along intersecting planes, which significantly complicates the process of grain deformation.
Therefore, starting from point B
the strength of the metal increases.
Surface defects
include mainly grain boundaries (Fig. 1.13). At the boundaries, the crystal lattice is highly distorted. Dislocations moving from inside the grains accumulate in them.
It is known from practice that fine-grained metal is stronger than coarse-grained metal. Since the latter has a smaller total length (area) of boundaries. We can conclude that surface defects help increase the strength of the metal. Therefore, several technological methods for producing fine-grained alloys have been created.
Fig.1.13. Structure of the boundary of two adjacent crystal grains
Volumetric defects
crystal lattice include cracks and pores. The presence of these defects, reducing the density of the metal, reduces its strength.
In addition, cracks are strong stress concentrators, increasing the stresses created in the metal by work loads by tens or more times. The latter circumstance most significantly affects the strength of the metal.