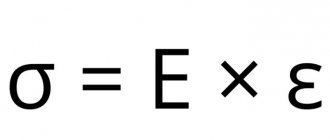All solids, both crystalline and amorphous, have the property of changing their shape under the influence of force applied to them. In other words, they are subject to deformation. If a body returns to its original size and shape after the external force ceases its influence, then it is called elastic, and its deformation is considered elastic. For any body, there is a limit to the applied force, after which the deformation ceases to be elastic, the body does not return to its original shape and original dimensions, but remains in a deformed state or collapses. The theory of elastic deformations of bodies was created at the end of the 17th century by the British scientist R. Hooke and developed in the works of his compatriot Thomas Young. Hooke's and Young's law and coefficient, which determine the degree of elasticity of bodies, were named in their honor, respectively. It is actively used in engineering during calculations of the strength of structures and products.
Basic information
Young's modulus (also called the longitudinal modulus of elasticity and the modulus of elasticity of the first kind) is an important mechanical characteristic of a substance. It is a measure of resistance to longitudinal deformation and determines the degree of rigidity. It is designated as E; measured in n/m 2 or in Pa.
This important coefficient is used when calculating the rigidity of workpieces, assemblies and structures, and in determining their resistance to longitudinal deformations. Substances used for the manufacture of industrial and building structures, as a rule, have very large E values. And therefore, in practice, E values for them are given in gigaPascals (10 12 Pa)
The value of E for rods can be calculated; for more complex structures it is measured during experiments.
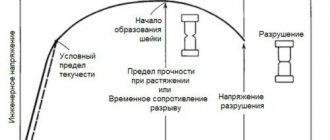
Approximate values of E can be obtained from the graph constructed during tensile tests.
Tensile test schedule
E is the quotient of normal stress σ divided by relative elongation ε.
Hooke's law can also be formulated using Young's modulus.
Physical meaning of Young's modulus
During a forced change in the shape of objects, forces are generated inside them that resist such a change and strive to restore the original shape and size of elastic bodies.
If the body does not resist changing shape and remains in a deformed form after the end of the impact, then such a body is called absolutely inelastic, or plastic. A typical example of a plastic body is a block of plasticine.
R. Hooke studied the elongation of rods made of various substances under the influence of weights suspended from the free end. The quantitative expression of the degree of change in shape is considered relative elongation, equal to the ratio of absolute elongation and original length.
As a result of a series of experiments, it was found that absolute elongation is proportional with the elasticity coefficient to the original length of the rod and the deforming force F and inversely proportional to the cross-sectional area of this rod S:
The inverse of α is called Young’s modulus:
ε = (Δl) / l = α * (F/S)
The ratio of tensile force F to S is called elastic stress σ:
Hooke's law, written using Young's modulus, looks like this:
Now we can formulate the physical meaning of Young’s modulus: it corresponds to the stress caused by stretching a rod-shaped sample twice, provided its integrity is maintained.
In reality, the vast majority of samples fail before they have stretched to twice their original length. The value of E is calculated using the indirect method for small deformations.
Stiffness coefficient for elastic deformation of the rod along its axis k = (ES) / l
Young's modulus determines the magnitude of the potential energy of bodies or media subjected to elastic deformation.
Temperature dependence of Young's modulus
The temperature dependence of the elastic modulus of simple crystalline materials is explained on the basis that the elastic modulus is defined as the second derivative of the internal energy with respect to the corresponding deformation. Therefore, at temperatures ( - Debye temperature), the temperature dependence of the elastic modulus is determined by the simple relation
where is the adiabatic modulus of elasticity of an ideal crystal at ; — module defect caused by thermal phonons; - module defect caused by thermal movement of conduction electrons
Young's modulus values for some materials
The table shows the E values of a number of common substances.
| Material | Young's modulus E, GPa |
| Aluminum | 70 |
| Bronze | 75-125 |
| Tungsten | 350 |
| Graphene | 1000 |
| Brass | 95 |
| Ice | 3 |
| Copper | 110 |
| Lead | 18 |
| Silver | 80 |
| Gray cast iron | 110 |
| Steel | 200/210 |
| Glass | 70 |
The longitudinal elastic modulus of steel is twice the Young's modulus of copper or cast iron. Young's modulus is widely used in formulas for strength calculations of structural elements and products in general.
Material tensile strength
This is the limit of the stress that occurs, after which the sample begins to fail.
Static tensile strength is measured under prolonged application of deforming force, dynamic - under short-term, impact nature of such force. For most substances the dynamic limit is greater than the static limit.
Read also: Do-it-yourself sandblasting from a freon cylinder
Tensile strength tool
In addition, there are limits to the material's compressive and tensile strength. They are determined experimentally on a test bench, by stretching or compressing samples with powerful hydraulic machines equipped with precise dynamometers and pressure meters. If it is impossible to achieve the required pressure hydraulically, a directed explosion in a sealed capsule is sometimes used.
Allowable tensile stress in some materials
From life experience we know that different materials resist changes in shape in different ways. The strength characteristics of crystalline and other solids are determined by the forces of interatomic interaction. As interatomic distances increase, the forces that attract atoms to each other also increase. These forces reach a maximum at a certain amount of stress, equal to approximately one tenth of Young's modulus.
Tensile test
This value is called theoretical strength; when it is exceeded, the destruction of the material begins. In reality, destruction begins at lower values, since the structure of real samples is heterogeneous. This causes an uneven distribution of stresses, and destruction begins from those areas where the stresses are maximum.
| Materials | σrast | |
| Bor | 5700 | 0,083 |
| Graphite | 2390 | 0,023 |
| Sapphire | 1495 | 0,030 |
| Steel wire | 415 | 0,01 |
| Fiberglass | 350 | 0,034 |
| Structural steel | 60 | 0,003 |
| Nylon | 48 | 0,0025 |
These numbers are taken into account by designers when choosing the material for parts of a future product. Strength calculations are also carried out using them. For example, cables used for lifting and transport operations must have a tenfold safety margin. They are periodically checked by hanging a load ten times greater than the cable's rated load capacity.
The safety margins built into critical structures are also multiple.
Mechanical properties: plasticity, elasticity, strength,
deformation, hardness
The properties of a material to resist mechanical stress are necessary for all structural materials. Resistance can cause deformations (dents, bends), which are called plastic and, if these deformations do not disappear after removing the load, they are called irreversible or residual.
The main characteristics of the deformative properties of a building material are the elastic modulus, ultimate deformation and creep.
The modulus of elasticity characterizes the measure of the rigidity of a material and is determined by the deformation of the material under gradual loading. The higher the strength of the material, the higher the elastic modulus and the lower the relative deformations. Deformations occur due to the convergence of atoms under load, which leads to a change in the size of the sample.
Elastic modulus E (MPa) relates elastic deformation and uniaxial stress (load) by the ratio:
The elasticity of a solid is the ability to restore its original shape and size after the cessation of external force. This deformation is called reversible.
The maximum deformations allowed during the operation of the structure are different for each material. For heavy concrete, they are 0.0015-0.003 m/m in compression, and ten times less in tension.
If their development is allowed to exceed this value, then microcracks appear, which subsequently leads to destruction.
Strength is an important property for structural materials. It characterizes the ability to resist the effects of internal stresses caused by external forces (load, impact, pressure). Most often, structures work in compression or tension.
All stone materials (natural or artificial) have good resistance to compression, and worse resistance to tension (in accordance with the maximum permissible deformations), so structures that operate under compression are made from them.
More plastic materials, such as wood, steel, and plastics, are used to make structures that are subject to both compression and tension.
The compressive or tensile stress is equal in magnitude to the force acting on 1 cm2 of the cross-sectional area (F) of the material (σ or Rcom) in kg/cm2 or MPa:
To determine the strength of stone building materials, prototypes of certain sizes are made in accordance with the standard: cubes (to determine the compressive strength of concrete) with edge lengths of 10, 15, and 20 cm; natural stone is tested on cores drilled from dense rocks; bending strength is determined on prisms made specifically for concrete with a cross-sectional cube size of 40, 60 or 80 cm, respectively.
The brick is a standard sample, so it is first tested in bending, then the halves, folded like a cube, are tested in compression. Compression is accompanied by transverse expansion of the material, to a greater extent closer to the middle of the sample, i.e.
further from the press plates. Frictional forces act between the press plates and the sample, preventing the expansion of the material due to compressive forces.
Therefore, cubes are tested in compression rather than prisms; when the expansion area is larger, this means that the compressive strength will be underestimated.
When testing the same material, cubes of different sizes also give different results. In order to be able to objectively evaluate the strength on cubes of different sizes, there are scale factors adopted for a cube size of 15x15x15 cm equal to unity; for a cube 10×10×10 cm – 0.95; for a cube Strength decreases when materials get wet; this is especially noticeable for materials with a lower density, which is why they are not used to make structures that operate in a damp environment. The decrease in the strength of a material after wetting is determined by the softening coefficient, equal to the ratio of the strength of the wet to the strength of the dry material:
Specific strength or structural quality factor is estimated for structural materials in relation to the strength to the density of the material.
The most effective materials are those with high strength and low density:
So, concrete M 400 has a specific strength:
for steel:
The theoretical strength of a homogeneous material is characterized by the stress required to separate two adjacent layers of atoms. The closer and denser the atoms are located in a material, the more difficult it is to separate them, and the more energy must be spent to destroy the material.
In the conditions of production of building materials from dissimilar components under different modes and technologies, with existing defects in the material at the molecular level, it is not possible to obtain materials of theoretical strength.
With the development of nanotechnology, when it becomes possible to influence the packing density of the smallest particles, the coefficient of structural quality of materials will increase.
Hardness is the property of a material to resist the penetration of another harder body into it.
Hardness is determined using a device - a hardness meter and is compared on the Mohs scale with the hardness of natural stone materials from the softest mineral talc (taken as 1) to the hardest mineral diamond (taken as 10).
The harder the material, the better it resists abrasion. This test is carried out on materials intended for floors, road surfaces, and stair steps.
Safety factor
To quantify the safety factor during design, a safety factor is used. It characterizes the product’s ability to withstand overloads above rated loads. For household products it is small, but for critical components and parts that, if destroyed, can pose a danger to human life and health, it is made multiple times.
Accurate calculation of strength characteristics makes it possible to create a sufficient safety margin and at the same time not to overweight the structure, worsening its performance characteristics. For such calculations, complex mathematical methods and sophisticated software are used. The most important designs are calculated on supercomputers.
Methods for determining and monitoring strength indicators of metals
The development of metallurgy and other related areas for the production of metal objects is due to the creation of weapons. At first they learned to smelt non-ferrous metals, but the strength of the products was relatively low. Only with the advent of iron and its alloys did the study of their properties begin.
The first swords were made quite heavy to give them hardness and strength. Warriors had to take them in both hands to control them.
Over time, new alloys appeared and production technologies were developed. Light sabers and swords came to replace heavy weapons. At the same time, tools were created.
With the increase in strength characteristics, tools and production methods were improved.
Relationship with other elastic moduli
Young's modulus is related to the shear modulus, which determines the ability of a sample to resist shear deformation, by the following relationship:
E is also associated with the bulk modulus of elasticity, which determines the sample’s ability to resist simultaneous compression from all sides.
If you find an error, please select a piece of text and press Ctrl+Enter.
One of the main tasks of engineering design is the choice of structural material and optimal profile section. It is necessary to find the size that, with the minimum possible mass, will ensure that the system maintains its shape under load.
For example, what number of steel I-beam should be used as a span beam for a structure? If we take a profile with dimensions smaller than required, we are guaranteed to get the destruction of the structure. If it is more, then this leads to irrational use of metal, and, consequently, heavier construction, more complicated installation, and increased financial costs. Knowledge of such a concept as the modulus of elasticity of steel will answer the above question and will allow you to avoid the occurrence of these problems at a very early stage of production.
General concept
The modulus of elasticity (also known as Young's modulus) is one of the indicators of the mechanical properties of a material, which characterizes its resistance to tensile deformation. In other words, its value shows the ductility of the material. The greater the elastic modulus, the less any rod will stretch, all other things being equal (load magnitude, cross-sectional area, etc.).
In the theory of elasticity, Young's modulus is denoted by the letter E. It is an integral part of Hooke's law (the law on the deformation of elastic bodies). Connects the stress arising in the material and its deformation.
According to the international standard system of units, it is measured in MPa. But in practice, engineers prefer to use the dimension kgf/cm2.
The elastic modulus is determined experimentally in scientific laboratories. The essence of this method is to tear dumbbell-shaped samples of material using special equipment. Having found out the stress and elongation at which the sample failed, divide these variables by each other, thereby obtaining Young's modulus.
Let us immediately note that this method is used to determine the elastic moduli of plastic materials: steel, copper, etc. Brittle materials - cast iron, concrete - are compressed until cracks appear.
Additional characteristics of mechanical properties
The modulus of elasticity makes it possible to predict the behavior of a material only when working in compression or tension. In the presence of such types of loads as crushing, shear, bending, etc., additional parameters will need to be introduced:
- Stiffness is the product of the elastic modulus and the cross-sectional area of the profile. By the value of rigidity, one can judge the plasticity not of the material, but of the structure as a whole. Measured in kilograms of force.
- Relative longitudinal elongation shows the ratio of the absolute elongation of the sample to the total length of the sample. For example, a certain force was applied to a rod 100 mm long. As a result, it decreased in size by 5 mm. Dividing its elongation (5 mm) by the original length (100 mm) we obtain a relative elongation of 0.05. A variable is a dimensionless quantity. In some cases, for ease of perception, it is converted to percentages.
- Relative transverse elongation is calculated similarly to the point above, but instead of length, the diameter of the rod is considered here. Experiments show that for most materials, transverse elongation is 3-4 times less than longitudinal elongation.
- The Punch ratio is the ratio of the relative longitudinal strain to the relative transverse strain. This parameter allows you to fully describe the change in shape under the influence of load.
- The shear modulus characterizes the elastic properties when the sample is exposed to tangential stresses, i.e., in the case when the force vector is directed at 90 degrees to the surface of the body. Examples of such loads are the work of rivets in shear, nails in crushing, etc. By and large, the shear modulus is associated with such a concept as the viscosity of the material.
- The bulk modulus of elasticity is characterized by a change in the volume of the material for uniform, versatile application of load. It is the ratio of volumetric pressure to volumetric compressive strain. An example of such work is a sample lowered into water, which is subject to liquid pressure over its entire area.
Read also: Causes of car compressor not working
In addition to the above, it should be mentioned that some types of materials have different mechanical properties depending on the direction of loading. Such materials are characterized as anisotropic. Vivid examples are wood, laminated plastics, some types of stone, fabrics, etc.
Isotropic materials have the same mechanical properties and elastic deformation in any direction. These include metals (steel, cast iron, copper, aluminum, etc.), non-laminated plastics, natural stones, concrete, rubber.
Mechanical properties
Only when working in tension or compression does the (Young's) modulus of elasticity help to predict the behavior of a particular material. But for bending, shearing, crushing and other loads, you will need to enter additional parameters:
- Stiffness is the product of the profile cross-section and the elastic modulus. By this value one can judge the plasticity of the structural unit as a whole, and not about the material separately. The unit of measurement is kilograms force.
- Longitudinal elongation is the ratio of the absolute elongation of the sample material to its total length. For example, some force was applied to a rod whose length is 200 millimeters. As a result, it became shorter by 5 millimeters. As a result, the relative elongation will be equal to 0.05. This quantity is dimensionless. For more convenient perception, it is sometimes converted into percentages.
- Transverse relative elongation is calculated in the same way as longitudinal relative elongation, but instead of length, the diameter of the rod is taken. It was experimentally found that for a larger amount of material, the transverse elongation is approximately 4 times less than the longitudinal elongation.
- Poisson's ratio. This is the ratio of relative longitudinal to relative transverse strain. Using this value, it is possible to fully describe the changes in shape under the influence of load.
- The shear modulus describes the elastic properties under the influence of tangential properties on the sample. In other words, when the force vector is directed towards the surface of the body at 90 degrees. An example of such loads is the work of nails under crushing, rivets under shear, etc. This parameter is related to the viscosity of the material.
- The bulk modulus of elasticity characterizes the change in the volume of a sample for a versatile uniform application of load. This value is the ratio of volumetric pressure to volumetric compressive strain. As an example, we can consider a material lowered into water, which is subject to liquid pressure over its entire area.
In addition to all of the above, it is worth mentioning that some materials have different mechanical properties depending on the direction of the load. Such materials are called anisotropic. Examples of this are fabrics, some types of stone, laminated plastics, wood, etc.
Isotropic materials have the same mechanical properties and elastic deformation in any direction. Such materials include metals: aluminum, copper, cast iron, steel, etc., as well as rubber, concrete, natural stones, non-laminated plastics.
Elastic modulus value
It should be noted that Young's modulus is not a constant value. Even for the same material, it can fluctuate depending on the points at which the force is applied.
Some elastic-plastic materials have a more or less constant modulus of elasticity when working in both compression and tension: copper, aluminum, steel. In other cases, the elasticity may vary based on the shape of the profile.
Here are examples of Young's modulus values (in millions kgscm2) of some materials:
- White cast iron – 1.15.
- Gray cast iron -1.16.
- Brass – 1.01.
- Bronze – 1.00.
- Brick masonry - 0.03.
- Granite stonework - 0.09.
- Concrete – 0.02.
- Wood along the grain – 0.1.
- Wood across the grain – 0.005.
- Aluminum – 0.7.
Let's consider the difference in readings between elastic moduli for steels depending on the grade:
- High quality structural steel (20, 45) – 2.01.
- Standard quality steel (St. 3, St. 6) – 2.00.
- Low alloy steels (30ХГСА, 40Х) – 2.05.
- Stainless steel (12Х18Н10Т) – 2.1.
- Die steel (9ХМФ) – 2.03.
- Spring steel (60С2) – 2.03.
- Bearing steel (ШХ15) – 2.1.
Also, the value of the elastic modulus for steels varies depending on the type of rolled product:
- High strength wire – 2.1.
- Braided rope – 1.9.
- Cable with a metal core - 1.95.
As we can see, the deviations between steels in the values of elastic deformation moduli are small. Therefore, in most engineering calculations, errors can be neglected and the value E = 2.0 taken.
The development of metallurgy and other related areas for the production of metal objects is due to the creation of weapons. At first they learned to smelt non-ferrous metals, but the strength of the products was relatively low. Only with the advent of iron and its alloys did the study of their properties begin.
The first swords were made quite heavy to give them hardness and strength. Warriors had to take them in both hands to control them. Over time, new alloys appeared and production technologies were developed. Light sabers and swords came to replace heavy weapons. At the same time, tools were created. With increasing strength characteristics, tools and production methods were improved.
Modulus of elasticity of aluminum and aluminum alloys
Modulus of elasticity = Young's modulus
In the figure you can see that at the initial stage of the stress-strain curve, the increase in strain per unit increase in stress for aluminum and aluminum alloys occurs much faster than for steel - three times.
The slope of this part of the curve determines the characteristic of the material - the elastic modulus (Young's modulus). Since the unit of measurement of strain is a dimensionless quantity, the dimension of Young's modulus coincides with the dimension of stress.
The Young's modulus of aluminum is approximately one-third that of steel and for most aluminum alloys is between 65,500 and 72,400 MPa. See Modulus of Elasticity of Various Aluminum Alloys
It is clear that if a steel beam is replaced with an aluminum alloy beam of identical shape, its weight will be three times less, but its elastic deflection under the same load will be approximately three times greater.
It can be noted that in this case, an aluminum beam of the same dimensions as a steel beam absorbs three times more energy, but only as long as the stresses in the aluminum alloy remain below the elastic limit.
Rigidity of aluminum profiles
It is worth noting that the rigidity of a structural element is defined as the product of the elastic modulus of the material and the moment of inertia of the element’s section (E × I), and the deflection of the element under the influence of a bending load depends on the rigidity.
This gives aluminum a chance to compete with steel: extruded aluminum profiles can have much more complex cross sections and thereby compensate for the low modulus of elasticity of aluminum by increasing the moment of inertia of their cross sections. In addition to bending rigidity, other factors must be taken into account, such as torsional rigidity.
As a result of all this, the complexity of the cross-section of the profile increases and often “eats” part of the expected weight gain, which is usually about 50% instead of the possible 33%.
The tables present the typical strength characteristics of popular wrought aluminum alloys: tensile strength, yield strength and tensile elongation, as well as fatigue strength, hardness and elastic modulus - separately for work harden alloys and heat treatable alloys. As typical properties they are only suitable for comparative purposes and not for engineering calculations. In most cases, they are average values for various product sizes, shapes and manufacturing methods.
Source: Aluminum and Aluminum Alloys. - ASM International, 1993.
Source: https://uvakin.ru/modul-uprugosti-alyuminiya-i-alyuminievyx-splavov/
Types of loads
When using metals, different static and dynamic loads are applied. In the theory of strength, it is customary to define the following types of loads.
- Compression - an acting force compresses an object, causing a decrease in length along the direction of application of the load. This deformation is felt by frames, supporting surfaces, racks and a number of other structures that can withstand a certain weight. Bridges and crossings, car and tractor frames, foundations and reinforcement - all these structural elements are under constant compression.
Read also: Specific gravity of lead g cm3
- Tension - the load tends to lengthen the body in a certain direction. Lifting and transport machines and mechanisms experience similar loads when lifting and carrying loads.
- Shear and shear - such loading is observed in the case of forces directed along the same axis towards each other. Connecting elements (bolts, screws, rivets and other hardware) experience this type of load. The design of housings, metal frames, gearboxes and other components of mechanisms and machines necessarily contains connecting parts. The performance of devices depends on their strength.
- Torsion - if a pair of forces acting on an object are located at a certain distance from each other, then a torque occurs. These forces tend to produce torsional deformation. Similar loads are observed in gearboxes; the shafts experience just such a load. It is most often inconsistent in meaning. Over time, the magnitude of the acting forces changes.
- Bending – a load that changes the curvature of objects is considered bending. Bridges, crossbars, consoles, lifting and transport mechanisms and other parts experience similar loading.
The concept of elastic modulus
In the middle of the 17th century, materials research began simultaneously in several countries. A variety of methods have been proposed for determining strength characteristics. The English researcher Robert Hooke (1660) formulated the main provisions of the law on the elongation of elastic bodies as a result of the application of a load (Hooke's law). The following concepts were also introduced:
- Stress σ, which in mechanics is measured in the form of a load applied to a certain area (kgf/cm², N/m², Pa).
- Elastic modulus E, which determines the ability of a solid body to deform under loading (applying force in a given direction). Units of measurement are also defined in kgf/cm² (N/m², Pa).
The formula according to Hooke's law is written as ε = σz/E, where:
- ε – relative elongation;
- σz – normal stress.
Demonstration of Hooke's law for elastic bodies:
From the above dependence, the value of E for a certain material is derived experimentally, E = σz/ε.
In the theory of strength, the concept of Young's modulus of elasticity is adopted. This English researcher gave a more specific description of the methods of changing strength indicators under normal loads.
The elastic modulus values for some materials are given in Table 1.
Table 1: Modulus of elasticity for metals and alloys
| Name of material | Elastic modulus value, 10¹² Pa |
| Aluminum | 65…72 |
| Duralumin | 69…76 |
| Iron, carbon content less than 0.08% | 165…186 |
| Brass | 88…99 |
| Copper (Cu, 99%) | 107…110 |
| Nickel | 200…210 |
| Tin | 32…38 |
| Lead | 14…19 |
| Silver | 78…84 |
| Gray cast iron | 110…130 |
| Steel | 190…210 |
| Glass | 65…72 |
| Titanium | 112…120 |
| Chromium | 300…310 |
Table of material elasticity indicators
Before moving directly to this characteristic of steel, let us first consider, as an example and additional information, a table containing data on this value in relation to other materials. The data is measured in MPa .
Modulus of elasticity of various materials
As you can see from the table above, this value is different for different materials, and the indicators also differ, if we take into account one or another option for calculating this indicator.
Everyone is free to choose exactly the option for studying indicators that suits them best. It may be preferable to consider Young’s modulus, since it is most often used specifically to characterize a particular material in this regard. After we have briefly reviewed the data on this characteristic of other materials, we will move directly to the characteristics of steel separately.
First, let's look at the hard numbers and derive different indicators of this characteristic for different types of steels and steel structures:
- Modulus of elasticity (E) for casting, hot-rolled reinforcement from steel grades called St.3 and St. 5 equals 2.1*106 kg/cm^2.
- For steels such as 25G2S and 30KhG2S this value is 2*106 kg/cm^2.
- For periodic wire and cold-drawn round wire, there is an elasticity value equal to 1.8 * 106 kg/cm^2. For cold-flattened reinforcement the indicators are similar.
- For strands and bundles of high-strength wire the value is 2·10 6 kg/cm^2
- For steel spiral ropes and ropes with a metal core, the value is 1.5·10 4 kg/cm^2, while for cables with an organic core this value does not exceed 1.3·10 6 kg/cm^2.
- The shear modulus (G) for rolled steel is 8.4·10 6 kg/cm^2.
- And finally, Poisson’s ratio for steel is equal to 0.3
These are general data given for types of steel and steel products. Each value was calculated in accordance with all physical rules and taking into account all existing relationships that are used to derive the values of this characteristic.
Below will be given all the general information about this characteristic of steel. Values will be given both by Young's modulus and by shear modulus, both in some units (MPa) and others (kg/cm2, newton*m2).
Elastic modulus for different steel grades
Metallurgists have developed several hundred grades of steel. They have different strength values. Table 2 shows the characteristics for the most common steels.
Table 2: Elasticity of steels
| Name of steel | Elastic modulus value, 10¹² Pa |
| Low carbon steel | 165…180 |
| Steel 3 | 179…189 |
| Steel 30 | 194…205 |
| Steel 45 | 211…223 |
| Steel 40Х | 240…260 |
| 65G | 235…275 |
| X12MF | 310…320 |
| 9ХС, ХВГ | 275…302 |
| 4Х5МФС | 305…315 |
| 3Х3М3Ф | 285…310 |
| R6M5 | 305…320 |
| P9 | 320…330 |
| P18 | 325…340 |
| R12MF5 | 297…310 |
| U7, U8 | 302…315 |
| U9, U10 | 320…330 |
| U11 | 325…340 |
| U12, U13 | 310…315 |
Video: Hooke's law, modulus of elasticity.
Torsional modulus of elasticity G, kN/mm2, at temperature, °C
| Grade of steel, alloy | 20°C | 100°C | 200°C | 300°C | 400°C | 500°C | 600°C | 700°C | 800°C |
| St5ps | 81 | 80 | 77 | 74 | 71 | 67 | 62 | — | — |
| St5sp | 81 | 80 | 77 | 74 | 71 | 67 | 62 | — | — |
| St6ps | 82 | 80 | 77 | 74 | 71 | 67 | 62 | — | — |
| St6sp | 82 | 80 | 77 | 74 | 71 | 67 | 62 | — | — |
| 10 | 78 | 77 | 76 | 73 | 69 | 66 | 59 | — | — |
| 15 | 83 | 78 | 77 | 74 | 71 | 68 | 63 | — | — |
| 15kp | 83 | 80 | 77 | 74 | 71 | 68 | 63 | — | — |
| 20 | 78 | 77 | 76 | 73 | 69 | 66 | 59 | — | — |
| 25 | 81 | 80 | 76 | 73 | 70 | 66 | 61 | — | — |
| 30 | 78 | 77 | 76 | 73 | 69 | 66 | 59 | — | — |
| 40 | 82 | 80 | 78 | 75 | 68 | 63 | 58 | 50 | 45 |
| 45 | 78 | — | — | 69 | — | 59 | — | — | — |
| 50 | 88 | 87 | 84 | 81 | 71 | 67 | 61 | 54 | 49 |
| 75 | 78 | — | — | — | — | — | — | — | — |
| 85 | 76 | — | — | — | — | — | — | — | — |
| 15K | 78 | 77 | 76 | 73 | 69 | 66 | 59 | — | — |
| 20K [3] | 80 | 79 | 78 | 74 | 70 | 68 | 60 | — | — |
| 22K [3] | 82 | 80 | — | 74 | — | 63 | — | — | — |
| 50G | 84 | 83 | 81 | 77 | 73 | 68 | 62 | 55 | 50 |
| 45G2 | 83 | — | — | — | — | — | — | — | — |
| 50G2 | 83 | — | — | — | — | — | — | — | — |
| 15X | 83 | 82 | 76 | 74 | 71 | 67 | 63 | 55 | 50 |
| 20X | 84 | 83 | 76 | 74 | 71 | 67 | 62 | 55 | 50 |
| 30X | 83 | — | — | — | — | — | — | — | — |
| 35X | 83 | — | — | — | — | — | — | — | — |
| 38ХА | 83 | — | — | — | — | — | — | — | — |
| 40X | 85 | 83 | 81 | 78 | 71 | 68 | 63 | 55 | 50 |
| 45X | 78 | — | — | — | — | — | — | — | — |
| 50X | 78 | — | — | — | — | — | — | — | — |
| 08GDNF | 83 | 81 | 78 | 73 | 67 | 64 | 59 | 52 | 48 |
| 09N2MFBA-A | 82 | — | — | — | — | — | — | — | — |
| 35ХМ | 82 | 83 | — | 75 | — | 66 | — | — | — |
| 38ХС | 84 | 80 | 78 | 72 | 68 | 65 | 62 | 55 | 48 |
| 14ХГС | 77 | — | — | — | — | — | — | — | — |
| 30ХГС, 30ХГСА | 84 | 82 | 79 | 75 | 71 | 66 | 62 | 54 | 47 |
| 35ХГСА | 84 | 82 | 79 | 76 | 71 | 66 | 62 | 54 | 47 |
| 18ХГТ | 84 | 80 | 77 | 75 | 68 | 66 | 59 | 52 | 49 |
| 30ХГТ | 83 | 79 | 76 | 74 | 67 | 66 | 61 | 53 | 51 |
| 15Х1М1Ф | 87 | 84 | 82 | 79 | 76 | 71 | 66 | 61 | — |
| 25Х1МФ (EI 10) | 82 | 80 | 77 | 75 | 71 | 65 | 63 | — | — |
| 34ХН1М, 34ХН1МА | 80 | 79 | 76 | 72 | 69 | 67 | 61 | — | — |
| 12ХН2 | 85 | 80 | 76 | 71 | 69 | 67 | 60 | 55 | 50 |
| 30ХН2МА | 80 | 79 | 76 | 72 | 69 | 67 | 61 | — | — |
| 40ХН2МА (40ХНМА) | 84 | 81 | 77 | 73 | 68 | 66 | — | — | — |
| 30HN2MFA (30HN2VFA) | 87 | 81 | 77 | 73 | 68 | 64 | — | — | — |
| 30KhGSN2A (30KhGSNA) | 77 | — | — | 70 | 65 | 51 | — | — | — |
| 20ХН3А | 83 | 80 | 76 | 70 | 68 | 66 | 59 | 53 | 51 |
| 30ХН3А | 84 | 81 | 76 | 72 | 67 | 65 | — | — | — |
| 34ХН3М, 34ХН3МА | 79 | 79 | — | — | 69 | 59 | — | — | — |
| 38ХН3МА | 82 | 80 | 77 | 76 | 72 | 69 | 66 | 57 | 53 |
| 38ХН3МФА | 83 | 80 | 77 | 73 | 68 | 64 | — | — | — |
| 25Х2М1Ф (EI 723) | 82 | 79 | 72 | 74 | 71 | 66 | 57 | — | — |
| 38Х2МУА (38ХМУА) | 82 | 79 | 76 | 75 | 71 | 66 | 62 | 57 | 53 |
| 25X2NMFA | 82 | 79 | 76 | 74 | 71 | 66 | 57 | — | — |
| 38Х2Н2МА (38ХНМА) | 84 | 80 | 76 | 71 | 67 | 63 | 59 | 59 | 48 |
| 65G | 84 | 83 | 80 | 77 | 70 | — | 58 | 51 | 48 |
| 40HFA | 84 | 83 | 80 | 77 | 71 | 66 | 64 | 56 | 52 |
| 55С2 | 78 | — | — | — | — | 65 | — | — | — |
| 60С2, 60С2А | 82 | 80 | 77 | 74 | 69 | 68 | 54 | 54 | 50 |
| ШХ15 | 80 | — | — | — | — | — | — | — | — |
| SHH15SG | 79 | — | — | — | — | — | — | — | — |
| 08Х13 (0Х13, EI 496) | 85 | 80 | 80 | 77 | 73 | 68 | 62 | — | — |
| 12Х13 (1Х13) | 85 | 80 | 80 | 77 | 73 | 68 | 62 | — | — |
| 20Х13 (2Х13) | 86 | 84 | 80 | 78 | 73 | 69 | 63 | — | — |
| 30Х13 (3Х13) | 86 | 84 | 81 | 77 | 74 | 69 | 64 | — | — |
| 03Х13Н8Д2ТМ (EP 699) | 83 | 82 | — | — | — | — | — | — | — |
| 05Х14Н5ДМ | 74 | — | — | — | — | — | — | — | — |
| 12X17 (X17, EZh17) | 93 | 89 | 85 | 82 | 78 | 75 | 69 | 61 | — |
| 12Х18Н9Т (Х18Н9Т) | 77 | — | — | — | — | — | — | — | — |
| 12Х18Н10Т | 77 | 74 | 71 | 67 | 63 | 59 | 57 | 54 | 49 |
| 12Х18Н12Т (Х18Н12Т) | 77 | — | — | — | — | — | — | — | — |
| 31Х19Н9МВБТ (ЭИ 572) | 78 | — | — | 68 | 65 | 62 | 58 | 54 | — |
| 12X25N16G7AR (EI 835) | 86 | — | — | — | — | — | — | — | — |
| 03Н18К9М5Т | 71 | — | — | — | — | — | — | — | — |
| U8, U8A | 81 | 80 | 77 | 74 | 71 | 67 | 62 | — | — |
| U9, U9A | 79 | — | — | — | — | — | — | — | — |
| U12, U12A | 82 | 80 | 78 | 75 | 72 | 69 | 63 | — | — |
| 9ХС | 79 | — | — | — | — | — | — | — | — |
| R6M5K5 | 83 | — | — | — | — | — | — | — | — |
| P9 | 83 | — | — | — | — | — | — | — | — |
| R9M4K8 | 87 | — | — | — | — | — | — | — | — |
| P12 | 88 | — | — | — | — | — | — | — | — |
| P18 | 83 | — | — | — | — | — | — | — | — |
| 20L | 78 | 76 | 73 | 71 | 67 | 63 | 58 | 50 | 45 |
| 35L | 82 | 80 | 78 | 75 | 68 | 63 | 58 | 50 | 45 |
| 50L | 85 | 83 | 81 | 76 | 69 | 65 | 59 | 52 | 46 |
| 70L | 78 | — | — | — | — | — | — | — | — |
| 08GDNFL | 83 | 81 | 78 | 73 | 67 | 64 | 59 | 52 | 48 |
| 08G2DNFL | 84 | — | — | — | — | — | — | — | — |
| 32Х06Л | 84 | 82 | 80 | 76 | 68 | 66 | 63 | 55 | 49 |
| 40HL | 85 | 84 | 81 | 78 | 71 | 68 | 63 | 54 | 50 |
| 35HML | 83 | 81 | 79 | 77 | 74 | 69 | 63 | 53 | 49 |
| 15Х1М1ФЛ | 87 | 84 | 82 | 79 | 76 | 71 | 66 | 61 | — |
| 35ХГСЛ | 84 | 82 | 79 | 76 | 71 | 66 | 62 | 54 | 47 |
| 15Х13Л | 85 | 80 | 80 | 77 | 73 | 68 | 63 | — | — |
| 20Х13Л | 87 | 84 | 82 | 79 | 76 | 71 | 64 | 55 | 53 |
| 12Х18Н9ТЛ | 76 | 73 | 68 | 63 | 59 | 52 | 50 | 47 | 42 |
| KHN70VMUT (EI 765) | 85 | 84 | 81 | 78 | 76 | 72 | 70 | 67 | 66 |
| N70MFV-VI (EP 814A-VI) | 230 | — | — | — | — | — | — | — | — |
| KHN58VKMTUBL (TsNK 8MP) | 80 | — | — | — | — | — | — | — | — |
| KHN65VMTYUL (EI 893L) | 83 | 82 | 80 | 77 | 74 | 71 | 68 | 65 | 62 |
| AD, AD00, AD0, AD1 [4] | 27 | — | — | — | — | — | — | — | — |
| BrB2 | 45,0 | — | — | — | — | — | — | — | — |
| VT1-0 | 39,2 | — | — | — | — | — | — | — | — |
| VT1-00 | 39,2 | — | — | — | — | — | — | — | — |
| VT5-1 | 44,1 | — | — | — | — | — | — | — | — |
| OT4 | 41,2 | — | — | — | — | — | — | — | — |
| OT4-0 | 44,1 | — | — | — | — | — | — | — | — |
| OT4-1 | 44,1 | — | — | — | — | — | — | — | — |
- Brand of steels and alloys. 2nd ed., corrected. and additional / Zubchenko A.S., Koloskov M.M., Kashirsky Yu.V. and others. Ed. A.S. Zubchenko. M.: Mechanical Engineering, 2003. 784 p.
- Mechanical engineering. Encyclopedia. T. II–3. Non-ferrous metals and alloys. Composite metal materials. /Under the general editorship of I.N. Friedlander. M.: Mechanical Engineering, 2001. 880 p.
- Zhuravlev V.N., Nikolaeva O.I. Engineering steels. Directory. 4th ed., revised. and additional M.: Mechanical Engineering, 1992. 480 p.
- Mikhailov-Mikheev P.B. Handbook of metal materials for turbine and engine construction. M.: Mashgiz, 1961. 838 p.
Source
Strength modules
In addition to normal loading, there are other force effects on materials.
The shear modulus G determines the stiffness. This characteristic shows the maximum load value for changing the shape of an object.
The bulk modulus of elasticity K determines the elastic properties of a material to change volume. With any deformation, the shape of the object changes.
For different steels, the values of the indicated modules are given in Table 3.
Table 3: Strength moduli for steels
| Name of steel | Young's modulus of elasticity, 10¹² Pa | Shear modulus G, 10¹² Pa | Modulus of bulk elasticity, 10¹² Pa | Poisson's ratio, 10¹²·Pa |
| Low carbon steel | 165…180 | 87…91 | 45…49 | 154…168 |
| Steel 3 | 179…189 | 93…102 | 49…52 | 164…172 |
| Steel 30 | 194…205 | 105…108 | 72…77 | 182…184 |
| Steel 45 | 211…223 | 115…130 | 76…81 | 192…197 |
| Steel 40Х | 240…260 | 118…125 | 84…87 | 210…218 |
| 65G | 235…275 | 112…124 | 81…85 | 208…214 |
| X12MF | 310…320 | 143…150 | 94…98 | 285…290 |
| 9ХС, ХВГ | 275…302 | 135…145 | 87…92 | 264…270 |
| 4Х5МФС | 305…315 | 147…160 | 96…100 | 291…295 |
| 3Х3М3Ф | 285…310 | 135…150 | 92…97 | 268…273 |
| R6M5 | 305…320 | 147…151 | 98…102 | 294…300 |
| P9 | 320…330 | 155…162 | 104…110 | 301…312 |
| P18 | 325…340 | 140…149 | 105…108 | 308…318 |
| R12MF5 | 297…310 | 147…152 | 98…102 | 276…280 |
| U7, U8 | 302…315 | 154…160 | 100…106 | 286…294 |
| U9, U10 | 320…330 | 160…165 | 104…112 | 305…311 |
| U11 | 325…340 | 162…170 | 98…104 | 306…314 |
| U12, U13 | 310…315 | 155…160 | 99…106 | 298…304 |
For other materials, strength characteristics are indicated in specialized literature. However, in some cases individual studies are carried out. Such research is especially relevant for building materials. At enterprises where reinforced concrete products are produced, tests are regularly carried out to determine limit values.
Young's modulus of elasticity and shear, Poisson's ratio values (Table)
Below are reference tables for commonly used constants; if two of them are known, then this is quite sufficient to determine the elastic properties of a homogeneous isotropic solid.
Young's modulus or modulus of longitudinal elasticity in dyn/cm2.
Shear modulus or torsional modulus G in dyn/cm2.
Compressive modulus or bulk modulus K in dynes/cm2.
Compressibility volume k=1/K/.
Poisson's ratio µ is equal to the ratio of transverse relative compression to longitudinal relative tension.
For a homogeneous isotropic solid material, the following relationships between these constants hold:
G = E / 2(1 + μ) - (α)
μ = (E / 2G) - 1 - (b)
K = E / 3(1 - 2μ) - (c)
Poisson's ratio has a positive sign and its value is usually between 0.25 and 0.5, but in some cases it can go beyond these limits. The degree of agreement between the observed values of µ and those calculated using formula (b) is an indicator of the isotropy of the material.
Tables of Young's Modulus of Elasticity, Shear Modulus and Poisson's Ratio
Values calculated from relations (a), (b), (c) are given in italics.
| Material at 18°C | Young's modulus E, 1011 dynes/cm2. | Shear modulus G, 1011 dynes/cm2. | Poisson's ratio µ | Modulus of bulk elasticity K, 1011 dynes/cm2. |
| Aluminum | 7,05 | 2,62 | 0,345 | 7,58 |
| Bismuth | 3,19 | 1,20 | 0,330 | 3,13 |
| Iron | 21,2 | 8,2 | 0,29 | 16,9 |
| Gold | 7,8 | 2,7 | 0,44 | 21,7 |
| Cadmium | 4,99 | 1,92 | 0,300 | 4,16 |
| Copper | 12,98 | 4,833 | 0,343 | 13,76 |
| Nickel | 20,4 | 7,9 | 0,280 | 16,1 |
| Platinum | 16,8 | 6,1 | 0,377 | 22,8 |
| Lead | 1,62 | 0,562 | 0,441 | 4,6 |
| Silver | 8,27 | 3,03 | 0,367 | 10,4 |
| Titanium | 11,6 | 4,38 | 0,32 | 10,7 |
| Zinc | 9,0 | 3,6 | 0,25 | 6,0 |
| Steel (1% C) 1) | 21,0 | 8,10 | 0,293 | 16,88 |
| (soft) | 21,0 | 8,12 | 0,291 | 16,78 |
| Constantan 2) | 16,3 | 6,11 | 0,327 | 15,7 |
| Manganin | 12,4 | 4,65 | 0,334 | 12,4 |
| 1) For steel containing about 1% C, elastic constants are known to change during heat treatment. 2) 60% Cu, 40% Ni. |
The experimental results given below are for common laboratory materials, mainly wires.
| Substance | Young's modulus E, 1011 dynes/cm2. | Shear modulus G, 1011 dynes/cm2. | Poisson's ratio µ | Modulus of bulk elasticity K, 1011 dynes/cm2. |
| Bronze (66% Cu) | -9,7-10,2 | 3,3-3,7 | 0,34-0,40 | 11,2 |
| Copper | 10,5-13,0 | 3,5-4,9 | 0,34 | 13,8 |
| Nickel silver1) | 11,6 | 4,3-4,7 | 0,37 | — |
| Glass | 5,1-7,1 | 3,1 | 0,17-0,32 | 3,75 |
| Glass yen crowns | 6,5-7,8 | 2,6-3,2 | 0,20-0,27 | 4,0-5,9 |
| Jena flint glass | 5,0-6,0 | 2,0-2,5 | 0,22-0,26 | 3,6-3,8 |
| Welding iron | 19-20 | 7,7-8,3 | 0,29 | 16,9 |
| Cast iron | 10-13 | 3,5-5,3 | 0,23-0,31 | 9,6 |
| Magnesium | 4,25 | 1,63 | 0,30 | — |
| Phosphor bronze2) | 12,0 | 4,36 | 0,38 | — |
| Platinoid3) | 13,6 | 3,6 | 0,37 | — |
| Quartz threads (floating) | 7,3 | 3,1 | 0,17 | 3,7 |
| Soft vulcanized rubber | 0,00015-0,0005 | 0,00005-0,00015 | 0,46-0,49 | — |
| Steel | 20-21 | 7,9-8,9 | 0,25-0,33 | 16,8 |
| Zinc | 8,7 | 3,8 | 0,21 | — |
| 1) 60% Cu, 15% Ni, 25% Zn2) 92.5% Cu, 7% Sn, 0.5% P3) Nickel silver with a small amount of tungsten. |
| Substance | Young's modulus E, 1011 dynes/cm2. | Substance | Young's modulus E, 1011 dynes/cm2. |
| Zinc (pure) | 9,0 | Oak | 1,3 |
| Iridium | 52,0 | Pine | 0,9 |
| Rhodium | 29,0 | Red tree | 0,88 |
| Tantalum | 18,6 | Zirconium | 7,4 |
| Invar | 17,6 | Titanium | 10,5-11,0 |
| Alloy 90% Pt, 10% Ir | 21,0 | Calcium | 2,0-2,5 |
| Duralumin | 7,1 | Lead | 0,7-1,6 |
| Silk threads1 | 0,65 | Teak | 1,66 |
| Web2 | 0,3 | Silver | 7,1-8,3 |
| Catgut | 0,32 | Plastics: | |
| Ice (-20C) | 0,28 | Thermoplastic | 0,14-0,28 |
| Quartz | 7,3 | Thermoset | 0,35-1,1 |
| Marble | 3,0-4,0 | Tungsten | 41,1 |
| 1) Reduces rapidly with increasing load 2) Detects noticeable elastic fatigue |
| Temperature coefficient (at 150C)Et=E11 (1-ɑ (t-15)), Gt=G11 (1-ɑ (t-15)) | Compressibility k, bar-1 (at 7-110C) | |||
| ɑ, for E | ɑ, for G | |||
| Aluminum | 4,8*10-4 | 5,2*10-4 | Aluminum | 1,36*10-6 |
| Brass | 3,7*10-4 | 4,6*10-4 | Copper | 0,73*10-6 |
| Gold | 4,8*10-4 | 3,3*10-4 | Gold | 0,61*10-6 |
| Iron | 2,3*10-4 | 2,8*10-4 | Lead | 2,1*10-6 |
| Steel | 2,4*10-4 | 2,6*10-4 | Magnesium | 2,8*10-6 |
| Platinum | 0,98*10-4 | 1,0*10-4 | Platinum | 0,36*10-6 |
| Silver | 7,5*10-4 | 4,5*10-4 | Flint glass | 3,0*10-6 |
| Tin | — | 5,9*10-4 | German glass | 2,57*10-6 |
| Copper | 3,0*10-4 | 3,1*10-4 | Steel | 0,59*10-6 |
| Nickel silver | — | 6,5*10-4 | ||
| Phosphor bronze | — | 3,0*10-4 | ||
| Quartz threads | -1,5*10-4 | -1,1*10-4 |
Source: https://infotables.ru/fizika/295-uprugie-svojstva-tel