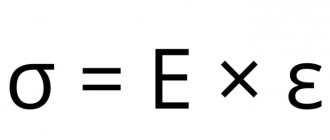Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.
Основные сведения
Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м 2 или в Па.
Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (10 12 Па)
Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.
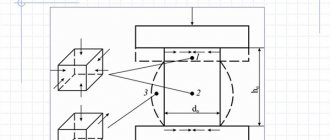
Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.
График теста на растяжение
E- это частное от деления нормальных напряжений σ на относительное удлинение ε.
Закон Гука также можно сформулировать и с использованием модуля Юнга.
Физический смысл модуля Юнга
Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.
Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.
Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.
В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:
Величину, обратную α, и называют модулем Юнга:
ε = (Δl) / l = α * (F/S)
Отношение растягивающей силы F к S называют упругим напряжением σ:
Закон Гука, записанный с использованием модуля Юнга, выглядит так:
Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.
В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.
Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l
Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.
Температурная зависимость модуля Юнга
Температурная зависимость модуля упругости простых кристаллических материалов объясняется исходя из того, что модуль упругости определяется как вторая производная от внутренней энергии по соответствующей деформации . Поэтому при температурах ( — температура Дебая) температурная зависимость модуля упругости определяется простым соотношением
где — адиабатический модуль упругости идеального кристалла при ; — дефект модуля, обусловленный тепловыми фононами; — дефект модуля, обусловленный тепловым движением электронов проводимости
Значения модуля юнга для некоторых материалов
В таблице показаны значения E ряда распространенных веществ.
| Материал | модуль Юнга E, ГПа |
| Алюминий | 70 |
| Бронза | 75-125 |
| Вольфрам | 350 |
| Графен | 1000 |
| Латунь | 95 |
| Лёд | 3 |
| Медь | 110 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 200/210 |
| Стекло | 70 |
Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.
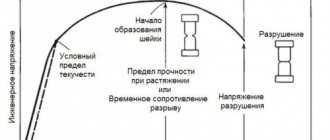
Предел прочности материала
Это предел возникающего напряжения, после которого образец начинает разрушаться.
Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.
Читать также: Пескоструй своими руками из баллона фреона
Инструмент для определения предела прочности
Кроме того, существуют пределы прочности на сжатие материала и на растяжение. Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.
Допускаемое механическое напряжение в некоторых материалах при растяжении
Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.
Испытание на растяжение
Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.
| Материалы | σраст | |
| Бор | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловолокно | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
Запасы прочности, закладываемые в ответственные конструкции, также многократны.
Механические свойства: пластичность, упругость, прочность,
деформации, твёрдость
Свойства материала сопротивляться механическим воздействиям необходимы всем конструкционным материалам. Сопротивление может вызывать деформации (вмятины, изгибы), которые называют пластическими и, если эти деформации после снятия нагрузки не исчезают, их называют необратимыми или остаточными.
Основной характеристикой деформативных свойств строительного материала является модуль упругости, предельные деформации и ползучесть.
Модуль упругости характеризует меру жёсткости материала и определяется с помощью деформации материала при постепенном нагружении его. Чем выше прочность материала, тем выше модуль упругости и меньше относительные деформации. Деформации происходят вследствие сближения под нагрузкой атомов, что ведёт к изменению размера образца.
Модуль упругости Е (МПа) связывает упругую деформацию и одноосное напряжение (нагрузку) отношением:
Упругость твёрдого тела – это способность восстанавливать первоначальную форму и размеры после прекращения действия внешней силы. Такую деформацию называют обратимой.
Предельные деформации, допускаемые при работе конструкции, у каждого материала свои. Для тяжёлого бетона они составляют при сжатии 0,0015-0,003 м/м, при растяжении – в десять раз меньше.
Если допускается их развитие больше этой величины, то появляются микротрещины, что в дальнейшем приводит к разрушению.
Прочность – важное свойство для конструкционных материалов. Оно характеризует способность сопротивляться действиям внутренних напряжений, вызванных внешними силами (нагрузкой, ударом, давлением). Чаще всего конструкции работают на сжатие или на растяжение.
Все каменные материалы (естественные или искусственные) хорошо сопротивляются сжатию, хуже – растяжению (в соответствии с предельно допустимыми деформациями), поэтому из них делают конструкции, работающие при сжатии.
Из материалов более пластичных, таких как: древесина, сталь, пластики делают конструкции, подвергающиеся и сжатию и растяжению.
Напряжение сжатия или растяжения по величине равно силе, действующей на 1 см2 площади сечения (F) материала (σ или Rсж) в кг/см2 или МПа:
Для определения прочности каменных строительных материалов изготавливают в соответствии со стандартом опытные образцы определённых размеров: кубики (для определения прочности при сжатии бетонов) с длиной ребра 10, 15, и 20 см; естественный камень испытывают на кернах, выбуренных из плотных пород; прочность при изгибе определяют на призмах, изготавливаемых специально для бетона с размером сечения кубиков длиной 40, 60 или 80 см соответственно.
Кирпич является стандартным образцом, поэтому его испытывают сначала на изгиб, затем половинки, сложенные как кубик, испытывают при сжатии. Сжатие сопровождается поперечным расширением материала, в большей степени ближе к середине образца, т. е.
дальше от плит пресса. Между плитами пресса и образцом действуют силы трения, препятствующие расширению материала от сжимающих сил.
Поэтому испытывают при сжатии кубики, а не призмы, когда область расширения будет больше, значит, прочность при сжатии будет занижена.
Кубики разных размеров при испытании одного материала тоже дают разный результат. Чтобы можно было объективно оценивать прочность на кубиках разных размеров, существуют масштабные коэффициенты, принятые для размера кубика 15×15×15 см равными единице; для кубика 10×10×10 см – 0,95; для кубика Прочность снижается при намокании материалов, у материалов с меньшей плотностью это особенно заметно, поэтому из них не делают конструкций, работающих во влажной среде. Снижение прочности материала после намокания определяют по коэффициенту размягчения, равному отношению прочности влажного к прочности сухого материала:
Удельная прочность или коэффициент конструктивного качества оценивается для конструктивных материалов по отношению прочности к плотности материала.
Наиболее эффективными считают материалы с высокой прочностью и низкой плотностью:
Так, у бетона М 400 удельная прочность:
у стали:
Теоретическая прочность однородного материала характеризуется напряжением, необходимым для разделения двух примыкающих слоёв атомов. Чем ближе и плотнее расположены атомы в материале, тем труднее их разделить, тем больше энергии надо потратить для разрушения материала.
В условиях производства строительных материалов из разнородных компонентов при разных режимах и технологиях, с имеющимися дефектами в материале на молекулярном уровне, получить материалы теоретической прочности не представляется возможным.
С развитием нанотехнологии, когда становится возможным влиять на плотность упаковки мельчайших частиц, коэффициент конструктивного качества материалов возрастёт.
Твёрдость – свойство материала сопротивляться проникновению в него другого более твёрдого тела.
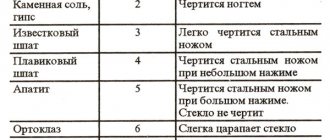
Твёрдость определяют на приборе – твердомере и сравнивают по шкале Мооса с твёрдостью природных каменных материалов от самого мягкого минерала талька, (принятого за 1), до самого твёрдого минерала алмаза, (принятого за 10).
Чем твёрже материал, тем лучше он сопротивляется истиранию. Этому испытанию подвергают материалы, предназначенные для пола, дорожных покрытий, лестничных ступеней.
Коэффициент запаса прочности
Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.
Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.
Способы определения и контроля показателей прочности металлов
Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.
Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними.
Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда.
С повышением прочностных характеристик совершенствовались инструменты и способы производства.
Связь с другими модулями упругости
Модуль Юнга связан с модулем сдвига, определяющим способность образца к сопротивлению против деформации сдвига, следующим соотношением:
E связан также и с модулем объёмной упругости, определяющим способность образца к сопротивлению против одновременного сжатия со всех сторон.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Одной из главных задач инженерного проектирования является выбор материала конструкции и оптимального сечения профиля. Необходимо найти тот размер, который при минимально возможной массе будет обеспечивать сохранение формы системы под воздействием нагрузки.
Например, какой номер стального двутавра использовать в качестве пролетной балки сооружения? Если взять профиль размерами ниже требуемого, то гарантировано получим разрушение строения. Если больше, то это ведет к нерациональному использованию металла, а, следовательно, утяжелению конструкции, усложнению монтажа, увеличению финансовых затрат. Знание такого понятия как модуль упругости стали даст ответ на вышепоставленный вопрос, и позволит избежать появления данных проблем на самом раннем этапе производства.
Общее понятие
Модуль упругости (также известный как модуль Юнга) – один из показателей механических свойств материала, который характеризует его сопротивляемость деформации растяжения. Другими словами, его значение показывает пластичность материала. Чем больше модуль упругости, тем менее будет растягиваться какой-либо стержень при прочих равных условиях (величина нагрузки, площадь сечения и прочее).
В теории упругости модуль Юнга обозначается буквой Е. Является составной частью закона Гука (закона о деформации упругих тел). Связывает напряжение, возникающее в материале, и его деформацию.
Согласно международной стандартной системе единиц измеряется в МПа. Но на практике инженеры предпочитают использовать размерность кгс/см2.
Определение модуля упругости осуществляется опытным путем в научных лабораториях. Суть данного способа заключается в разрыве на специальном оборудовании гантелеобразных образцов материала. Узнав напряжение и удлинение, при котором произошло разрушение образца, делят данные переменные друг на друга, тем самым получая модуль Юнга.
Отметим сразу, что таким методом определяются модули упругости пластичных материалов: сталь, медь и прочее. Хрупкие материалы – чугун, бетон – сжимают до появления трещин.
Дополнительные характеристики механических свойств
Модуль упругости дает возможность предугадать поведение материла только при работе на сжатие или растяжение. При наличии таких видов нагрузок как смятие, срез, изгиб и прочее потребуется введение дополнительных параметров:
- Жесткость есть произведение модуля упругости на площадь поперечного сечения профиля. По величине жесткости можно судить о пластичности уже не материала, а узла конструкции в целом. Измеряется в килограммах силы.
- Относительное продольное удлинение показывает отношение абсолютного удлинения образца к общей длине образца. Например, к стержню длиной 100 мм приложили определенную силу. Как результат, он уменьшился в размере на 5 мм. Деля его удлинение (5 мм) на первоначальную длину (100 мм) получаем относительное удлинение 0,05. Переменная является безразмерной величиной. В некоторых случаях для удобства восприятия переводится в проценты.
- Относительное поперечное удлинение рассчитывается аналогично вышепредставленному пункту, но вместо длины здесь рассматривается диаметр стержня. Опыты показывают, что для большинства материалов поперечное удлинение в 3-4 раза меньше, чем продольное.
- Коэффициент Пуансона есть отношение относительной продольной деформации к относительной поперечной деформации. Данный параметр позволяет полностью описать изменение формы под воздействием нагрузки.
- Модуль сдвига характеризует упругие свойства при воздействии на образец касательных напряжений, т. е. в случае, когда вектор силы направлен под 90 градусов к поверхности тела. Примерами таких нагрузок является работа заклепок на срез, гвоздей на смятие и прочее. По большому счету, модуль сдвига связан с таким понятием как вязкость материла.
- Модуль объемной упругости характеризуется изменением объема материала для равномерного разностороннего приложения нагрузки. Является отношением объемного давления к объемной деформации сжатия. Примером такой работы служит опущенный в воду образец, на который по всей его площади воздействует давление жидкости.
Читать также: Не работает автомобильный компрессор причины
Помимо вышесказанного необходимо упомянуть, что некоторые типы материалов имеют различные механические свойства в зависимости от направления нагрузки. Такие материалы характеризуются как анизотропные. Яркими примерами служит древесина, слоистые пластмассы, некоторые виды камня, ткани и прочее.
У изотропных материалов механические свойства и упругая деформация одинаковы в любом направлении. К ним относят металлы (сталь, чугун, медь, алюминий и прочее), неслоистые пластмассы, естественные камни, бетон, каучук.
Механические свойства
Только при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала. А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры:
- Жёсткостью называют произведение поперечного сечения профиля на модуль упругости. По этой величине можно судить о пластичности узла конструкции в целом, а не о материале отдельно. Единицей измерения являются килограммы силы.
- Продольное относительное удлинение — это отношение абсолютного удлинения материала-образца к его общей длине. К примеру, на стержень, длина которого равна 200 миллиметров, приложили некоторую силу. В результате он стал короче на 5 миллиметров. В результате относительное удлинение будет равняться 0,05. Эта величина безразмерная. Для более удобного восприятия иногда её переводят в проценты.
- Поперечное относительное удлинение рассчитывается точно так же, как и продольное относительное удлинение, но вместо длины берут диаметр стержня. Опытным путём было установлено, что для большего количества материала поперечное меньше продольного удлинения приблизительно в 4 раза.
- Коэффициент Пуассона. Это отношения относительной продольной к относительной поперечной деформации. При помощи этой величины можно полностью описать под воздействием нагрузки изменения формы.
- Модуль сдвига описывает упругие свойства под воздействием касательных свойств на образец. Иными словами, когда вектор силы направляется к поверхности тела под 90 градусов. Примером подобных нагрузок служит работа гвоздей на смятие, заклёпок на срез и пр. Этот параметр связан с вязкостью материала.
- Модуль упругости объёмной характеризует изменение объёма образца для разностороннего равномерного приложения нагрузки. Эта величина является отношением давления объёмного к деформации сжатия объёмной. Как пример можно рассматривать опущенный в воду материал, на который воздействует давление жидкости по всей его площади.
Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства. Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.
У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.
Значение модуля упругости
Необходимо заметить, что модуль Юнга не является постоянной величиной. Даже для одного и того же материала он может колебаться в зависимости от точек приложения силы.
Некоторые упруго – пластичные материалы обладают более или менее постоянным модулем упругости при работе как на сжатие, так и на растяжение: медь, алюминий, сталь. В других случаях упругость может изменяться исходя из формы профиля.
Вот примеры значений модуля Юнга (в миллионах кгссм2) некоторых материалов:
- Чугун белый – 1,15.
- Чугун серый -1,16.
- Латунь – 1,01.
- Бронза – 1,00.
- Кирпичная каменная кладка – 0,03.
- Гранитная каменная кладка – 0,09.
- Бетон – 0,02.
- Древесина вдоль волокон – 0,1.
- Древесина поперек волокон – 0,005.
- Алюминий – 0,7.
Рассмотрим разницу в показаниях между модулями упругости для сталей в зависимости от марки:
- Стали конструкционные высокого качества (20, 45) – 2,01.
- Стали обычного качества (Ст.3, Ст.6) – 2,00.
- Стали низколегированные (30ХГСА, 40Х) – 2,05.
- Стали нержавеющие (12Х18Н10Т) – 2,1.
- Стали штамповые (9ХМФ) – 2,03.
- Стали пружинные (60С2) – 2,03.
- Стали подшипниковые (ШХ15) – 2,1.
Также значение модуля упругости для сталей изменяется исходя из вида проката:
- Проволока высокой прочности – 2,1.
- Плетенный канат – 1,9.
- Трос с металлическим сердечником – 1,95.
Как видим, отклонения между сталями в значениях модулей упругой деформации имеют небольшую величину. Поэтому в большинстве инженерных расчетов можно пренебречь погрешностями и брать значение Е=2,0.
Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.
Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними. Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда. С повышением прочностных характеристик совершенствовались инструменты и способы производства.
Модуль упругости алюминия и алюминиевых сплавов
Модуль упругости = Модуль Юнга
На рисунке можно видеть, что на начальном этапе кривой напряжение-деформация увеличение деформации на единицу увеличения напряжения у алюминия и алюминиевых сплавов происходит намного быстрее, чем у стали – в три раза.
Наклон этой части кривой определяет характеристику материала — модуль упругости (модуль Юнга). Поскольку единица измерения деформации – безразмерная величина, то размерность модуля Юнга совпадает с размерностью напряжения.
Модуль Юнга алюминия составляет примерно одну треть от модуля Юнга стали и для большинства алюминиевых сплавов находится между 65500 и 72400 МПа. См. Модуль упругости различных алюминиевых сплавов
Ясно, что если стальную балку заменить на идентичную по форме балку из алюминиевого сплава, то вес ее будет в три раза меньше, но и ее упругий прогиб под той же нагрузкой будет приблизительно в три раза больше.
Можно отметить, что при этом алюминиевая балка тех же размеров, что и стальная балка поглощает в три раза больше энергии, но только до тех пор, пока напряжения в алюминиевом сплаве остаются ниже предела упругости.
Жесткость алюминиевых профилей
Стоит отметить, что жесткость конструкционного элемента определяется как произведение модуля упругости материала и момента инерции сечения элемента (E × I) и именно от жесткости зависит прогиб элемента под воздействием изгибающей нагрузки.
Это дает алюминию шанс в соревновании со сталью: прессованные алюминиевые профили могут иметь намного более сложные поперечные сечения и тем самым компенсировать малость модуля упругости алюминия увеличением момента инерции их поперечных сечений. Кроме жесткости на изгиб необходимо учитывать и другие факторы, например, жесткость на кручение.
В результате всего этого сложность поперечного сечения профиля возрастает и часто «съедает» часть ожидаемого выигрыша в весе, который обычно составляет около 50 % вместо возможных 33 %.
В таблицах представлены типичные прочностные характеристики популярных деформируемыхалюминиевых сплавов: предел прочности, предел текучести и удлинение при испытаниях на растяжение, а также усталостная прочность, твердость и модуль упругости – отдельно для сплавов, упрочняемых нагартовкой, и сплавов, упрочняемые термической обработкой. Как типичные свойства они годятся только для сравнительных целей, а не для инженерных расчетов. В большинстве случаев они являются средними значениями для различных размеров изделий, их форм и методов изготовления.
Источник: Aluminium and Aluminium Alloys. — ASM International, 1993.
Источник: https://uvakin.ru/modul-uprugosti-alyuminiya-i-alyuminievyx-splavov/
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
- Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.
Читать также: Удельный вес свинца г см3
- Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.
- Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
- Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
- Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.
Понятие о модуле упругости
В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
- Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
- Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).
Формула по закону Гука записывается в виде ε = σz/E, где:
- ε – относительное удлинение;
- σz – нормальное напряжение.
Демонстрация закона Гука для упругих тел:
Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.
В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.
Значения модуля упругости для некоторых материалов приведены в таблице 1.
Таблица 1: Модуль упругости для металлов и сплавов
| Наименование материала | Значение модуля упругости, 10¹²·Па |
| Алюминий | 65…72 |
| Дюралюминий | 69…76 |
| Железо, содержание углерода менее 0,08 % | 165…186 |
| Латунь | 88…99 |
| Медь (Cu, 99 %) | 107…110 |
| Никель | 200…210 |
| Олово | 32…38 |
| Свинец | 14…19 |
| Серебро | 78…84 |
| Серый чугун | 110…130 |
| Сталь | 190…210 |
| Стекло | 65…72 |
| Титан | 112…120 |
| Хром | 300…310 |
Таблица показателей упругости материалов
Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.
Модуль упругости различных материалов
Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.
После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.
Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:
- Модуль упругости (Е) для литья, горячекатанной арматуры из сталей марок, именуемых Ст.3 и Ст. 5 равняется 2,1*106 кг/см^2.
- Для таких сталей как 25Г2С и 30ХГ2С это значение равно 2*106 кг/см^2.
- Для проволоки периодического профиля и холоднотянутой круглой проволоки, существует такое значение упругости, равняющееся 1,8*106 кг/см^2. Для холодно-сплющенной арматуры показатели аналогичны.
- Для прядей и пучков высокопрочной проволоки значение равняется 2·10 6 кГ/см^2
- Для стальных спиральных канатов и канатов с металлическим сердечником значение равняется 1,5·10 4 кГ/см^2, в то время как для тросов с сердечником органическим это значение не превышает1,3·10 6 кГ/см^2 .
- Модуль сдвига (G) для прокатной стали равен 8,4·10 6 кГ/см^2 .
- И напоследок коэффициент Пуассона для стали равен значению 0,3
Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.
Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).
Модуль упругости для разных марок стали
Металлурги разработали несколько сотен марок сталей. Им свойственны разные значения прочности. В таблице 2 показаны характеристики для наиболее распространенных сталей.
Таблица 2: Упругость сталей
| Наименование стали | Значение модуля упругости, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 |
| Сталь 3 | 179…189 |
| Сталь 30 | 194…205 |
| Сталь 45 | 211…223 |
| Сталь 40Х | 240…260 |
| 65Г | 235…275 |
| Х12МФ | 310…320 |
| 9ХС, ХВГ | 275…302 |
| 4Х5МФС | 305…315 |
| 3Х3М3Ф | 285…310 |
| Р6М5 | 305…320 |
| Р9 | 320…330 |
| Р18 | 325…340 |
| Р12МФ5 | 297…310 |
| У7, У8 | 302…315 |
| У9, У10 | 320…330 |
| У11 | 325…340 |
| У12, У13 | 310…315 |
Видео: закон Гука, модуль упругости.
Модуль упругости при кручении G, кН/мм2, при температуре, °C
| Марка стали, сплава | 20°C | 100°C | 200°C | 300°C | 400°C | 500°C | 600°C | 700°C | 800°C |
| Ст5пс | 81 | 80 | 77 | 74 | 71 | 67 | 62 | — | — |
| Ст5сп | 81 | 80 | 77 | 74 | 71 | 67 | 62 | — | — |
| Ст6пс | 82 | 80 | 77 | 74 | 71 | 67 | 62 | — | — |
| Ст6сп | 82 | 80 | 77 | 74 | 71 | 67 | 62 | — | — |
| 10 | 78 | 77 | 76 | 73 | 69 | 66 | 59 | — | — |
| 15 | 83 | 78 | 77 | 74 | 71 | 68 | 63 | — | — |
| 15кп | 83 | 80 | 77 | 74 | 71 | 68 | 63 | — | — |
| 20 | 78 | 77 | 76 | 73 | 69 | 66 | 59 | — | — |
| 25 | 81 | 80 | 76 | 73 | 70 | 66 | 61 | — | — |
| 30 | 78 | 77 | 76 | 73 | 69 | 66 | 59 | — | — |
| 40 | 82 | 80 | 78 | 75 | 68 | 63 | 58 | 50 | 45 |
| 45 | 78 | — | — | 69 | — | 59 | — | — | — |
| 50 | 88 | 87 | 84 | 81 | 71 | 67 | 61 | 54 | 49 |
| 75 | 78 | — | — | — | — | — | — | — | — |
| 85 | 76 | — | — | — | — | — | — | — | — |
| 15К | 78 | 77 | 76 | 73 | 69 | 66 | 59 | — | — |
| 20К [3] | 80 | 79 | 78 | 74 | 70 | 68 | 60 | — | — |
| 22К [3] | 82 | 80 | — | 74 | — | 63 | — | — | — |
| 50Г | 84 | 83 | 81 | 77 | 73 | 68 | 62 | 55 | 50 |
| 45Г2 | 83 | — | — | — | — | — | — | — | — |
| 50Г2 | 83 | — | — | — | — | — | — | — | — |
| 15Х | 83 | 82 | 76 | 74 | 71 | 67 | 63 | 55 | 50 |
| 20Х | 84 | 83 | 76 | 74 | 71 | 67 | 62 | 55 | 50 |
| 30Х | 83 | — | — | — | — | — | — | — | — |
| 35Х | 83 | — | — | — | — | — | — | — | — |
| 38ХА | 83 | — | — | — | — | — | — | — | — |
| 40Х | 85 | 83 | 81 | 78 | 71 | 68 | 63 | 55 | 50 |
| 45Х | 78 | — | — | — | — | — | — | — | — |
| 50Х | 78 | — | — | — | — | — | — | — | — |
| 08ГДНФ | 83 | 81 | 78 | 73 | 67 | 64 | 59 | 52 | 48 |
| 09Н2МФБА-А | 82 | — | — | — | — | — | — | — | — |
| 35ХМ | 82 | 83 | — | 75 | — | 66 | — | — | — |
| 38ХС | 84 | 80 | 78 | 72 | 68 | 65 | 62 | 55 | 48 |
| 14ХГС | 77 | — | — | — | — | — | — | — | — |
| 30ХГС, 30ХГСА | 84 | 82 | 79 | 75 | 71 | 66 | 62 | 54 | 47 |
| 35ХГСА | 84 | 82 | 79 | 76 | 71 | 66 | 62 | 54 | 47 |
| 18ХГТ | 84 | 80 | 77 | 75 | 68 | 66 | 59 | 52 | 49 |
| 30ХГТ | 83 | 79 | 76 | 74 | 67 | 66 | 61 | 53 | 51 |
| 15Х1М1Ф | 87 | 84 | 82 | 79 | 76 | 71 | 66 | 61 | — |
| 25Х1МФ (ЭИ 10) | 82 | 80 | 77 | 75 | 71 | 65 | 63 | — | — |
| 34ХН1М, 34ХН1МА | 80 | 79 | 76 | 72 | 69 | 67 | 61 | — | — |
| 12ХН2 | 85 | 80 | 76 | 71 | 69 | 67 | 60 | 55 | 50 |
| 30ХН2МА | 80 | 79 | 76 | 72 | 69 | 67 | 61 | — | — |
| 40ХН2МА (40ХНМА) | 84 | 81 | 77 | 73 | 68 | 66 | — | — | — |
| 30ХН2МФА (30ХН2ВФА) | 87 | 81 | 77 | 73 | 68 | 64 | — | — | — |
| 30ХГСН2А (30ХГСНА) | 77 | — | — | 70 | 65 | 51 | — | — | — |
| 20ХН3А | 83 | 80 | 76 | 70 | 68 | 66 | 59 | 53 | 51 |
| 30ХН3А | 84 | 81 | 76 | 72 | 67 | 65 | — | — | — |
| 34ХН3М, 34ХН3МА | 79 | 79 | — | — | 69 | 59 | — | — | — |
| 38ХН3МА | 82 | 80 | 77 | 76 | 72 | 69 | 66 | 57 | 53 |
| 38ХН3МФА | 83 | 80 | 77 | 73 | 68 | 64 | — | — | — |
| 25Х2М1Ф (ЭИ 723) | 82 | 79 | 72 | 74 | 71 | 66 | 57 | — | — |
| 38Х2МЮА (38ХМЮА) | 82 | 79 | 76 | 75 | 71 | 66 | 62 | 57 | 53 |
| 25Х2НМФА | 82 | 79 | 76 | 74 | 71 | 66 | 57 | — | — |
| 38Х2Н2МА (38ХНМА) | 84 | 80 | 76 | 71 | 67 | 63 | 59 | 59 | 48 |
| 65Г | 84 | 83 | 80 | 77 | 70 | — | 58 | 51 | 48 |
| 40ХФА | 84 | 83 | 80 | 77 | 71 | 66 | 64 | 56 | 52 |
| 55С2 | 78 | — | — | — | — | 65 | — | — | — |
| 60С2, 60С2А | 82 | 80 | 77 | 74 | 69 | 68 | 54 | 54 | 50 |
| ШХ15 | 80 | — | — | — | — | — | — | — | — |
| ШХ15СГ | 79 | — | — | — | — | — | — | — | — |
| 08Х13 (0Х13, ЭИ 496) | 85 | 80 | 80 | 77 | 73 | 68 | 62 | — | — |
| 12Х13 (1Х13) | 85 | 80 | 80 | 77 | 73 | 68 | 62 | — | — |
| 20Х13 (2Х13) | 86 | 84 | 80 | 78 | 73 | 69 | 63 | — | — |
| 30Х13 (3Х13) | 86 | 84 | 81 | 77 | 74 | 69 | 64 | — | — |
| 03Х13Н8Д2ТМ (ЭП 699) | 83 | 82 | — | — | — | — | — | — | — |
| 05Х14Н5ДМ | 74 | — | — | — | — | — | — | — | — |
| 12Х17 (Х17, ЭЖ17) | 93 | 89 | 85 | 82 | 78 | 75 | 69 | 61 | — |
| 12Х18Н9Т (Х18Н9Т) | 77 | — | — | — | — | — | — | — | — |
| 12Х18Н10Т | 77 | 74 | 71 | 67 | 63 | 59 | 57 | 54 | 49 |
| 12Х18Н12Т (Х18Н12Т) | 77 | — | — | — | — | — | — | — | — |
| 31Х19Н9МВБТ (ЭИ 572) | 78 | — | — | 68 | 65 | 62 | 58 | 54 | — |
| 12Х25Н16Г7АР (ЭИ 835) | 86 | — | — | — | — | — | — | — | — |
| 03Н18К9М5Т | 71 | — | — | — | — | — | — | — | — |
| У8, У8А | 81 | 80 | 77 | 74 | 71 | 67 | 62 | — | — |
| У9, У9А | 79 | — | — | — | — | — | — | — | — |
| У12, У12А | 82 | 80 | 78 | 75 | 72 | 69 | 63 | — | — |
| 9ХС | 79 | — | — | — | — | — | — | — | — |
| Р6М5К5 | 83 | — | — | — | — | — | — | — | — |
| Р9 | 83 | — | — | — | — | — | — | — | — |
| Р9М4К8 | 87 | — | — | — | — | — | — | — | — |
| Р12 | 88 | — | — | — | — | — | — | — | — |
| Р18 | 83 | — | — | — | — | — | — | — | — |
| 20Л | 78 | 76 | 73 | 71 | 67 | 63 | 58 | 50 | 45 |
| 35Л | 82 | 80 | 78 | 75 | 68 | 63 | 58 | 50 | 45 |
| 50Л | 85 | 83 | 81 | 76 | 69 | 65 | 59 | 52 | 46 |
| 70Л | 78 | — | — | — | — | — | — | — | — |
| 08ГДНФЛ | 83 | 81 | 78 | 73 | 67 | 64 | 59 | 52 | 48 |
| 08Г2ДНФЛ | 84 | — | — | — | — | — | — | — | — |
| 32Х06Л | 84 | 82 | 80 | 76 | 68 | 66 | 63 | 55 | 49 |
| 40ХЛ | 85 | 84 | 81 | 78 | 71 | 68 | 63 | 54 | 50 |
| 35ХМЛ | 83 | 81 | 79 | 77 | 74 | 69 | 63 | 53 | 49 |
| 15Х1М1ФЛ | 87 | 84 | 82 | 79 | 76 | 71 | 66 | 61 | — |
| 35ХГСЛ | 84 | 82 | 79 | 76 | 71 | 66 | 62 | 54 | 47 |
| 15Х13Л | 85 | 80 | 80 | 77 | 73 | 68 | 63 | — | — |
| 20Х13Л | 87 | 84 | 82 | 79 | 76 | 71 | 64 | 55 | 53 |
| 12Х18Н9ТЛ | 76 | 73 | 68 | 63 | 59 | 52 | 50 | 47 | 42 |
| ХН70ВМЮТ (ЭИ 765) | 85 | 84 | 81 | 78 | 76 | 72 | 70 | 67 | 66 |
| Н70МФВ-ВИ (ЭП 814А-ВИ) | 230 | — | — | — | — | — | — | — | — |
| ХН58ВКМТЮБЛ (ЦНК 8МП) | 80 | — | — | — | — | — | — | — | — |
| ХН65ВМТЮЛ (ЭИ 893Л) | 83 | 82 | 80 | 77 | 74 | 71 | 68 | 65 | 62 |
| АД, АД00, АД0, АД1 [4] | 27 | — | — | — | — | — | — | — | — |
| БрБ2 | 45,0 | — | — | — | — | — | — | — | — |
| ВТ1-0 | 39,2 | — | — | — | — | — | — | — | — |
| ВТ1-00 | 39,2 | — | — | — | — | — | — | — | — |
| ВТ5-1 | 44,1 | — | — | — | — | — | — | — | — |
| ОТ4 | 41,2 | — | — | — | — | — | — | — | — |
| ОТ4-0 | 44,1 | — | — | — | — | — | — | — | — |
| ОТ4-1 | 44,1 | — | — | — | — | — | — | — | — |
- Марочник сталей и сплавов. 2-е изд., исправл. и доп. / Зубченко А.С., Колосков М.М., Каширский Ю.В. и др. Под ред. А.С. Зубченко. М.: Машиностроение, 2003. 784 с.
- Машиностроение. Энциклопедия. Т. II–3. Цветные металлы и сплавы. Композиционные металлические материалы. /Под общей редакцией И.Н. Фридляндера. М.: Машиностроение, 2001. 880 с.
- Журавлев В.Н., Николаева О.И. Машиностроительные стали. Справочник. 4-е изд., перераб. и доп. М.: Машиностроение, 1992. 480 с.
- Михайлов-Михеев П.Б. Справочник по металлическим материалам турбино- и моторостроения. М.: Машгиз, 1961. 838 с.
Источник
Модули прочности
Кроме нормального нагружения, существуют и иные силовые воздействия на материалы.
Модуль сдвига G определяет жесткость. Эта характеристика показывает предельное значение нагрузки изменению формы предмета.
Модуль объемной упругости К определяет упругие свойства материала изменить объем. При любой деформации происходит изменение формы предмета.
Для разных сталей значения указанных модулей приведены в таблице 3.
Таблица 3: Модули прочности для сталей
| Наименование стали | Модуль упругости Юнга, 10¹²·Па | Модуль сдвига G, 10¹²·Па | Модуль объемной упругости, 10¹²·Па | Коэффициент Пуассона, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 | 87…91 | 45…49 | 154…168 |
| Сталь 3 | 179…189 | 93…102 | 49…52 | 164…172 |
| Сталь 30 | 194…205 | 105…108 | 72…77 | 182…184 |
| Сталь 45 | 211…223 | 115…130 | 76…81 | 192…197 |
| Сталь 40Х | 240…260 | 118…125 | 84…87 | 210…218 |
| 65Г | 235…275 | 112…124 | 81…85 | 208…214 |
| Х12МФ | 310…320 | 143…150 | 94…98 | 285…290 |
| 9ХС, ХВГ | 275…302 | 135…145 | 87…92 | 264…270 |
| 4Х5МФС | 305…315 | 147…160 | 96…100 | 291…295 |
| 3Х3М3Ф | 285…310 | 135…150 | 92…97 | 268…273 |
| Р6М5 | 305…320 | 147…151 | 98…102 | 294…300 |
| Р9 | 320…330 | 155…162 | 104…110 | 301…312 |
| Р18 | 325…340 | 140…149 | 105…108 | 308…318 |
| Р12МФ5 | 297…310 | 147…152 | 98…102 | 276…280 |
| У7, У8 | 302…315 | 154…160 | 100…106 | 286…294 |
| У9, У10 | 320…330 | 160…165 | 104…112 | 305…311 |
| У11 | 325…340 | 162…170 | 98…104 | 306…314 |
| У12, У13 | 310…315 | 155…160 | 99…106 | 298…304 |
Для других материалов значения прочностных характеристик указывают в специальной литературе. Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.
Модуль упругости Юнга и сдвига, коэффициент Пуассона значения (Таблица)
Ниже приводятся справочные таблицы общеупотребительных констант; если известны две их них, то этого вполне достаточно для определения упругих свойств однородного изотропного твердого тела.
Модуль Юнга или модуль продольной упругости в дин/см2.
Модуль сдвига или модуль кручения G в дин/см2.
Модуль всестороннего сжатия или модуль объемной упругости К в дин/см2.
Объем сжимаемости k=1/K/.
Коэффициент Пуассона µ равен отношению поперечного относительного сжатия к продольному относительному растяжению.
Для однородного изотропного твердого материала имеют место следующие соотношения между этими константами:
G = E / 2(1 + μ) — (α)
μ = (E / 2G) — 1 — (b)
K = E / 3(1 — 2μ) — (c)
Коэффициент Пуассона имеет положительный знак, и его значение обычно заключено в пределах от 0,25 до 0,5, но в некоторых случаях он может выходить за указанные пределы. Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.
Таблицы значений Модуля упругости Юнга, Модуля сдвига и коэффициента Пуассона
Курсивом даны значения, вычисленные из соотношений (a), (b), (c).
| Материал при 18°С | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
| Алюминий | 7,05 | 2,62 | 0,345 | 7,58 |
| Висмут | 3,19 | 1,20 | 0,330 | 3,13 |
| Железо | 21,2 | 8,2 | 0,29 | 16,9 |
| Золото | 7,8 | 2,7 | 0,44 | 21,7 |
| Кадмий | 4,99 | 1,92 | 0,300 | 4,16 |
| Медь | 12,98 | 4,833 | 0,343 | 13,76 |
| Никель | 20,4 | 7,9 | 0,280 | 16,1 |
| Платина | 16,8 | 6,1 | 0,377 | 22,8 |
| Свинец | 1,62 | 0,562 | 0,441 | 4,6 |
| Серебро | 8,27 | 3,03 | 0,367 | 10,4 |
| Титан | 11,6 | 4,38 | 0,32 | 10,7 |
| Цинк | 9,0 | 3,6 | 0,25 | 6,0 |
| Сталь (1% С) 1) | 21,0 | 8,10 | 0,293 | 16,88 |
| (мягкая) | 21,0 | 8,12 | 0,291 | 16,78 |
| Константан 2) | 16,3 | 6,11 | 0,327 | 15,7 |
| Манганин | 12,4 | 4,65 | 0,334 | 12,4 |
| 1) Для стали, содержащий около 1% С, упругие константы, как известно , меняются при термообработке.2) 60% Cu, 40% Ni. |
Экспериментальные результаты, приводимые ниже, относятся к обычным лабораторным материалам, главным образом проволокам.
| Вещество | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
| Бронза (66% Cu) | -9,7-10,2 | 3,3-3,7 | 0,34-0,40 | 11,2 |
| Медь | 10,5-13,0 | 3,5-4,9 | 0,34 | 13,8 |
| Нейзильбер1) | 11,6 | 4,3-4,7 | 0,37 | — |
| Стекло | 5,1-7,1 | 3,1 | 0,17-0,32 | 3,75 |
| Стекло иенское крон | 6,5-7,8 | 2,6-3,2 | 0,20-0,27 | 4,0-5,9 |
| Стекло иенское флинт | 5,0-6,0 | 2,0-2,5 | 0,22-0,26 | 3,6-3,8 |
| Железо сварочное | 19-20 | 7,7-8,3 | 0,29 | 16,9 |
| Чугун | 10-13 | 3,5-5,3 | 0,23-0,31 | 9,6 |
| Магний | 4,25 | 1,63 | 0,30 | — |
| Бронза фосфористая2) | 12,0 | 4,36 | 0,38 | — |
| Платиноид3) | 13,6 | 3,6 | 0,37 | — |
| Кварцевые нити (плав.) | 7,3 | 3,1 | 0,17 | 3,7 |
| Резина мягкая вулканизированная | 0,00015-0,0005 | 0,00005-0,00015 | 0,46-0,49 | — |
| Сталь | 20-21 | 7,9-8,9 | 0,25-0,33 | 16,8 |
| Цинк | 8,7 | 3,8 | 0,21 | — |
| 1) 60% Cu, 15% Ni, 25% Zn2) 92,5% Cu, 7% Sn, 0,5% P3) Нейзильбер с небольшим количеством вольфрама. |
| Вещество | Модуль Юнга E, 1011 дин/см2. | Вещество | Модуль Юнга E, 1011 дин/см2. |
| Цинк (чистый) | 9,0 | Дуб | 1,3 |
| Иридий | 52,0 | Сосна | 0,9 |
| Родий | 29,0 | Красное дерево | 0,88 |
| Тантал | 18,6 | Цирконий | 7,4 |
| Инвар | 17,6 | Титан | 10,5-11,0 |
| Сплав 90% Pt, 10% Ir | 21,0 | Кальций | 2,0-2,5 |
| Дюралюминий | 7,1 | Свинец | 0,7-1,6 |
| Шелковые нити1 | 0,65 | Тиковое дерево | 1,66 |
| Паутина2 | 0,3 | Серебро | 7,1-8,3 |
| Кетгут | 0,32 | Пластмассы: | |
| Лед (-20С) | 0,28 | Термопластичные | 0,14-0,28 |
| Кварц | 7,3 | Термореактивные | 0,35-1,1 |
| Мрамор | 3,0-4,0 | Вольфрам | 41,1 |
| 1) Быстро уменьшается с увеличением нагрузки2) Обнаруживает заметную упругую усталость |
| Температурный коэффициент (при 150С)Et=E11 (1-ɑ (t-15)), Gt=G11 (1-ɑ (t-15)) | Сжимаемость k, бар-1(при 7-110С) | |||
| ɑ, для Е | ɑ, для G | |||
| Алюминий | 4,8*10-4 | 5,2*10-4 | Алюминий | 1,36*10-6 |
| Латунь | 3,7*10-4 | 4,6*10-4 | Медь | 0,73*10-6 |
| Золото | 4,8*10-4 | 3,3*10-4 | Золото | 0,61*10-6 |
| Железо | 2,3*10-4 | 2,8*10-4 | Свинец | 2,1*10-6 |
| Сталь | 2,4*10-4 | 2,6*10-4 | Магний | 2,8*10-6 |
| Платина | 0,98*10-4 | 1,0*10-4 | Платина | 0,36*10-6 |
| Серебро | 7,5*10-4 | 4,5*10-4 | Стекло флинт | 3,0*10-6 |
| Олово | — | 5,9*10-4 | Стекло немецкое | 2,57*10-6 |
| Медь | 3,0*10-4 | 3,1*10-4 | Сталь | 0,59*10-6 |
| Нейзильбер | — | 6,5*10-4 | ||
| Фосфористая бронза | — | 3,0*10-4 | ||
| Кварцевые нити | -1,5*10-4 | -1,1*10-4 |
Источник: https://infotables.ru/fizika/295-uprugie-svojstva-tel