Weight of solid part
Home > Mass calculations > Solid part mass
05/09/2013 // Vladimir Trunov
This strange title of the article is explained only by the fact that parts of the same shape can be either solid or hollow (i.e. the next article will be called “Mass of a hollow part”).
Here is the time to remember that the mass of a body is its volume, multiplied by the density of its material (see density tables): The volume of a solid part is... its volume and nothing more.
Note : In the formulas below, all dimensions are measured in millimeters, and density is measured in grams per cubic centimeter. The letter indicates the ratio of the circumference of a circle to its diameter, which is approximately 3.14 .
Let's look at several simple forms (more complex ones, as you remember, can be made by adding or subtracting simple ones).
Mass of a parallelepiped (bar)
Volume of a parallelepiped: , where is the length, is the width, is the height. Then the mass:
Cylinder weight
Volume of the cylinder: , where is the diameter of the base, is the height of the cylinder. Then the mass:
Ball mass
Volume of the ball: , where is the diameter of the ball. Then the mass:
Ball segment mass
Volume of a ball segment: , where is the diameter of the base of the segment, and is the height of the segment. Then the mass:
Cone mass
The volume of any cone: , where is the area of the base, and is the height of the cone. For a round cone: , where is the diameter of the base, and is the height of the cone. Mass of round cone:
Mass of a truncated cone
Since it is impossible to embrace the immensity, we will consider only a round truncated cone. Its volume is the difference between the volumes of two nested cones: with bases and : , where , . After algebraic transformations that are not interesting to anyone, we get: , where is the diameter of the larger base, is the diameter of the smaller base, is the height of the truncated cone. Hence the mass:
Mass of the pyramid
The volume of any pyramid is equal to one third of the product of the area of its base and its height (the same as for cones (we often don’t notice how favorable the universe is to us)): , where is the area of the base and is the height of the pyramid. For a pyramid with a rectangular base: , where is the width, is the length, is the height of the pyramid. Then the mass of the pyramid is:
Mass of a truncated pyramid
Consider a truncated pyramid with a rectangular base. Its volume is the difference between the volumes of two similar pyramids with bases and: , where , . Having crossed out half of the notebook sheet, we get: , where , is the width and length of the larger base, , is the width and length of the smaller base, and is the height of the pyramid. And, leaving the remaining half of the sheet alone, based on symmetry considerations alone, we can write another formula, which differs from the previous one only by replacing W with L and vice versa. What is the difference between length and width? Only that we called them that. Let's call it the other way around and get: . Then the mass of a truncated rectangular pyramid is:
or
For a pyramid with a square base (, ), the formula looks simpler:
mass calculation
Weight of ring, link
Introduction to Mass Calculations
Plate weight
Related Posts
Determination of the mass of the product and the mass of blanks for its manufacture.
In conditions of large-scale and mass production, hot stamping, chill and pressure casting, shell molds and lost-wax casting are more cost-effective. Machining allowances are significantly reduced and the complexity of manufacturing parts is reduced.
B) Materials and requirements for the quality of parts
The material of the workpiece is determined by the purpose of the part or product, their design forms, serial production, the technical level of blank production and the economic feasibility of using a certain method of manufacturing the workpiece.
Until the recent past, mechanical engineering was dominated by universal materials, each of which was used under a wide variety of operating conditions. As the range of grades of cast iron, steel, etc., as well as non-metals, expanded, they began to be selected in accordance with the special requirements for the operation of the part. Materials must have the necessary reserve of certain technological properties: malleability, stampability, fluidity, weldability, machinability.
A necessary technological property for deformable materials is technological plasticity. The lower the plasticity of the material, the more difficult it is to obtain a high-quality workpiece by metal forming, the more complex the technical process, the higher the cost of the part.
Special requirements for the ductility of metals are imposed during cold forming of metals: extrusion, drawing, bending, molding.
If the material has reduced casting properties - low fluidity, high tendency to absorb gases and shrinkage, etc., it is not recommended to produce blanks from this material by die casting or under pressure, because Casting stresses, casting warpage, and cracks may occur. In such cases, it is better to use shell casting or casting in sand-clay molds. Alloys prone to increased gas absorption are undesirable for injection molding; For centrifugal casting, the use of alloys prone to segregation is excluded.
For critical, heavily loaded parts operating under variable loads, forgings are used as blanks, and the physical and mechanical properties of the material are significantly increased.
B) Dimensions, weight and configuration of the part
When designing products, it is necessary to focus on a specific manufacturing method and prefer such structural forms and elements of parts that most fully correspond to the chosen method of manufacturing parts, ensuring high levels of productivity, efficiency and accuracy.
The specific cost of castings and forgings increases with a decrease in their mass, especially sharply with a mass of up to 20 kg (since the labor intensity of shaping is determined by the total area of surfaces to be processed).
Reducing the material consumption of a product is the main factor in increasing the efficiency of machine-building production. Material costs range from 20 to 65% of the cost of the part.
Cutting should be used as little as possible; it is justified when performing small volumes of work and finishing operations, as well as to improve surface quality and dimensional accuracy.
For many casting methods, the dimensions of the casting are limited by the technical capabilities of the equipment, so the dimensions of the parts play a decisive role when choosing a method for producing blanks.
D) Surface quality of workpieces, ensuring specified accuracy.
The use of precise precision methods for producing workpieces ensures sufficient surface cleanliness and high accuracy of workpieces. Thus, the improvement of forging and stamping processes makes it possible to obtain workpieces whose surface roughness parameters and dimensional accuracy correspond to those achieved during machining, and in some cases during finishing operations (polishing).
Special types of stamping (calibration, cold extrusion) provide finished parts (rivets, nuts, bolts) and machine parts suitable for assembly without additional cutting processing. Most special types of casting (chill casting, shell mold casting, pressure casting, lost wax casting, liquid stamping, etc.) make it possible to obtain fairly accurate castings with dimensional accuracy of up to 12-15 quality and a roughness parameter Ra = 6.3 - 3, 2 microns.
E) Capabilities of existing equipment
The capabilities of the available equipment should be taken into account when producing workpieces by centrifugal casting, injection molding, hot stamping, etc. It is especially necessary to take into account the capabilities of the equipment when choosing a method for producing workpieces by metal forming. The presence of rotary forging machines in the forge shop makes it possible to produce step workpieces with virtually no mechanical processing; the same effect can be achieved with double-action mechanical presses or multi-stage hydraulic presses designed for stamping parts in split dies. If you have embossing presses, after hot die forging you can use embossing (calibration) as a finishing operation, which will significantly reduce the allowance for machining.
Example. Select a workpiece for a part such as a flange with a hole made of steel 40ХЛ, the mass of the finished part is 25 kg, most surfaces with a roughness Ra = 10 - 2.5 µm, dimensional accuracy 13-14 quality. Annual production program – 50,000 pcs.
In this case it is casting, because the casting grade of steel is specified. We determine the casting method. Because part weight – 25 kg, annual production program – 50,000 pieces, mass production. Here it is advisable to use special casting methods that ensure the specified accuracy, roughness, and dimensions. This includes die casting, shell mold casting, lost wax casting and pressure casting. We exclude injection molding - it has not been widely used in the casting of steel blanks due to the low durability of the casting equipment. For the same reason, casting in a chill mold is undesirable (the durability of the chill mold does not exceed 500 pieces)
Lost wax casting is expensive and labor-intensive; it is used in cases where it is impossible to obtain a workpiece by other means. This means that all that remains is casting into shell molds.
This selection technique is very inaccurate, so a technical and economic comparative analysis of the choice of workpiece is necessary.
⇐ Previous2Next ⇒
Recommended pages:
Calculation of the mass of a copper cylinder
Let's consider a simple problem. You need to find the mass of a cylinder made of copper. To be specific, let the cylinder have a diameter of 20 cm and a height of 10 cm.
Before you begin solving the problem, you should understand the initial data. The radius of the cylinder is equal to half its diameter, which means r = 20/2 = 10 cm, and the height is h = 10 cm. Since the cylinder considered in the problem is made of copper, then, referring to the reference data, we write down the density value of this material: ρ = 8 .96 g/cm3 (for temperature 20 °C).
Now you can start solving the problem. First, let's calculate the volume: V = pi*r2*h = 3.14*(10)2*10 = 3140 cm3. Then the mass of the cylinder will be equal to: m = ρ*V = 8.96 * 3140 = 28134 grams or approximately 28 kilograms.
Attention should be paid to the dimension of units when using them in the corresponding formulas. Thus, in the problem all parameters were presented in centimeters and grams.
What is a conversion factor
Let's complicate the task. Suppose you need to buy a sheet of non-ferrous metal. Let's use a conversion factor, which is the ratio of the density of a particular metal or alloy to the average density of steel. By multiplying the weight of a steel product of a certain range and size by the coefficient of the desired metal or alloy, we obtain the weight of the part.
| Name of metal or alloy | Coefficient |
| Aluminum | 0,34 |
| Copper | 1,14 |
| Brass LS59 | 1,08 |
| Bronze OTS 5-5-5 | 1,12 |
| Gray cast iron | 0,9 |
Example - let's calculate the mass of a bronze sheet with a thickness of 2 mm and an area of 2 m2.
7.85x2x2x1.12 = 35.2 kg
Attention! The same simple algorithm can be applied to non-metallic sheet materials, for which there are also conversion factors. For example, for rubber - 0.17-0.23, organic glass - 0.15, caprolon - 0.15, textolite - 0.18, rubber - 0.17-0.23.
Metal weight calculators
If you have access to the Internet, calculating the mass of rolled metal is not difficult. The metal calculator can be used online or downloaded to your computer.
How the calculation is performed:
- Select the type of rolled metal from the list.
- Fill in the data in the dimensions specified in the program.
- Press the calculation button.
- Calculators also usually indicate the weight of a linear meter of a specific assortment and the number of meters per ton.
Attention! All data provided by metal calculators is based on GOST. In the absence of tabular values, the mass is calculated using geometric formulas, adjusted for the manufacturing features of these products. In standard calculations, the density of steel is assumed to be 7,850 kg/m3.
The actual mass of rolled metal almost always differs from the theoretical one.
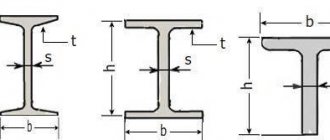
How to calculate the mass of an equal angle angle, channel, I-beam
The weight of a linear meter of corner metal depends on the width and thickness of the shelves.
Attention! The weight of a corner calculated using a geometric formula or determined from a table may differ greatly from the actual one. This is due to the fact that some manufacturers, in order to reduce the cost of products, reduce the thickness of the corner flange in places where verification measurements are not provided. Such a difference can significantly exceed the tolerances provided for by GOST.
Weight per linear meter of the most common range of equal-flange angles
| Shelf width, mm | Shelf thickness, mm | Weight of 1 m corner, kg | Shelf width, mm | Shelf thickness, mm | Weight of 1 m corner, kg |
| 20 | 3 | 0,89 | 40 | 3 | 1,85 |
| 20 | 4 | 1,15 | 40 | 4 | 2,42 |
| 25 | 3 | 1,12 | 45 | 3 | 2,08 |
| 25 | 4 | 1,46 | 45 | 4 | 2,73 |
| 32 | 3 | 1,46 | 50 | 3 | 2,32 |
| 32 | 4 | 1,91 | 50 | 4 | 3,05 |
| 36 | 3 | 1,65 | 63 | 4 | 3,9 |
| 36 | 4 | 2,16 | 63 | 5 | 4,81 |
It is difficult to independently calculate the mass of a channel and an I-beam due to the complex shape of the section. In this case, tables are used.
Channel weight table
| Profile number | Weight 1 m, kg | Profile number | Weight 1 m, kg | Profile number | Weight 1 m, kg |
| 5 | 4,84 | 12 | 10,4 | 20 | 18,4 |
| 6,5 | 5,9 | 14 | 12,3 | 22 | 21,0 |
| 8 | 7,05 | 16 | 14,2 | 24 | 24 ,0 |
| 10 | 8,59 | 18 | 16,3 | 27 | 27,7 |
I-beam weight table
| Profile number | Weight 1 m, kg | Profile number | Weight 1 m, kg | Profile number | Weight 1 m, kg |
| 10 | 9,46 | 18 | 18,4 | 27 | 31,5 |
| 12 | 11,5 | 20 | 21,0 | 30 | 36,5 |
| 14 | 13,7 | 22 | 24,0 | 33 | 42,2 |
| 16 | 15,9 | 24 | 27,3 | 36 | 48,6 |
We calculate the weight of rolled sheets
Definition! In all our calculations, the base value is the average density of steel - 7,850 kg/m3 according to the SI system.
First, let’s carry out a simple step - find out the mass of a square meter of steel sheet 1 mm thick. It looks like this - 1 m x 1 m x 0.001 m x 7850 kg/m3. That is, we multiplied the length, width and thickness of the sheet (all values were taken in meters), and we got the volume of the product. The product of volume and density gives mass - 7.85 kg. Thus, we found out that a square meter of steel sheet 1 mm thick weighs 7.85 kg.
And then all calculations are made by multiplying the value of 7.85 kg by the area and thickness of the real sheet. For example, you need to buy a sheet with a thickness of 4 mm and an area of 2 m2. The mass of such a product is determined by the formula 7.85x4x2 = 62.8 kg. A sheet of the same size, but 2 mm thick, weighs 7.85 x 2 x 2 = 31.4 kg.
If you are satisfied with the approximate calculation, round the value of 7.85 kg to 8 kg. Then calculations can be carried out even in your head without a calculator, and the error will be less than 2%.
We present the weights of steel sheets of the most popular sizes.
| Sheet thickness, mm | Sheet dimensions, m | Sheet weight, kg | Weight 1 m 2, kg |
| 0,35 | 1.0x2.0 | 5,5 | 2,75 |
| 0,35 | 1.25x2.5 | 8,59 | |
| 0,5 | 1.0x2.0 | 7,85 | 3,93 |
| 0,5 | 1.25x2.5 | 12,27 | |
| 0,8 | 1.0x2.0 | 12,56 | 6,28 |
| 0,8 | 1.25x2.5 | 19,63 | |
| 1,0 | 1.0x2.0 | 15,7 | 7,85 |
| 1,0 | 1.25x2.5 | 24,53 | |
| 1,5 | 1.0x2.0 | 23,55 | 11,78 |
| 1,5 | 1.25x2.5 | 36,8 | |
| 2,0 | 1.0x2.0 | 31,4 | 15,7 |
| 2,0 | 1.25x2.5 | 49,06 | |
| 2,5 | 1.0x2.0 | 39,25 | 19,63 |
| 2,5 | 1.25x2.5 | 61,33 | |
| 3,0 | 1.0x2.0 | 47,1 | 23,55 |
| 3,0 | 1.25x2.5 | 73,59 | |
| 3,5 | 1.25x2.5 | 85,86 | 27,48 |
| 4,0 | 1.5x6.0 | 282,6 | 31,4 |
| 5,0 | 1.5x6.0 | 353,25 | 39,25 |