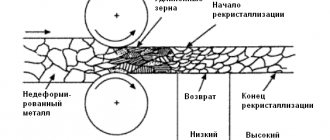
Heat treatment. To help the thermal worker

6. HOW AND WHY INTERNAL STRESSES ARISE DURING HARDENING

During hardening, internal stresses arise, which can be so large in magnitude that this leads to cracks and destruction of the steel without any additional impact. Warping of parts is also the result of internal stresses. There are three types of internal stress.

Stresses of the 1st kind.

The only reason for the occurrence of such stresses is the uneven cooling of parts during hardening. As we have already seen, the surface layers of the metal cool faster, the internal layers slower; Thin parts of the part cool faster, massive parts cool slower. Why does this lead to internal stress? Let's imagine a ring into which a rod is tightly inserted (Fig. 20). Place such a rod with a ring in a furnace and heat it to quenching temperature. Now let's unload them from the oven and start pouring a cold water shower over the ring. As the temperature decreases, the volume of the body, as is known, decreases (the body contracts). Consequently, when cooling, the ring should decrease in volume, and therefore in diameter. But the rod prevents this, since its temperature has hardly changed, which means the diameter has remained the same. Under these conditions, the ring begins to put pressure on the rod, compressing it from all sides. Therefore, compressive stresses arise in the rod. The ring may even break. Something similar can happen when placing a hot shell on a barrel. Thus, tensile stresses arise in the ring.

^A similar picture is obtained when hardening a solid cylindrical part (Fig. 21). Its outer surface in the form of an annular layer is cooled

quickly and decreases in volume. The inner zone cools slowly and therefore prevents compression of the outer annular layer. As a result, the inner zone of the metal will be compressed, and the outer zone will be stretched. In the subsequent period, the inner zone, cooling, will decrease in volume and pull the outer annular layer towards the center, tending to reduce its diameter. But the metal outside has already cooled down and therefore has lost its plasticity. Now the outer zone plays the role of a rigid ring, which can no longer decrease in diameter. Therefore, during the final cooling period, compressive stresses will arise in the outer layers of the metal. The inner zone of the metal, being connected to the outer layers, will not be able to decrease in volume, although it will tend to do so. As a result, tensile internal stresses will arise in it. Tensile stresses are more dangerous than compressive stresses. When hardening massive parts, when the difference in temperature between the internal and external layers reaches a significant value, such stresses can cause cracks or even lead to complete destruction of the metal, as is the case, for example, when hardening hammer dies.

Internal stresses of the 1st kind, as is now clear, are caused by volumetric changes in the metal when the temperature decreases or increases, and therefore they are called thermal stresses.

Stresses of the 2nd kind.

Such stresses are caused by structural changes during hardening. As already indicated, different steel structures have different specific volumes: martensite is the maximum, austenite is the minimum, and pearlite is the middle one between them.

Let's imagine a cylindrical part made of carbon steel that is not calcined through. Then, after quenching, the outer annular layer of such a part will have a martensitic structure, and the central part will have a pearlite structure. As martensite forms, the volume of steel increases, and therefore the outer martensite ring will tend to increase in diameter. But the central zone prevents this, trying to pull the ring towards the center. As a result, compressive stresses will arise in the outer martensitic layer of the metal, and, on the contrary, tensile stresses will arise in the central zone.

These stresses are also associated with changes in the volume of the metal, but such changes in this case are caused by structural transformations. That is why stresses are called structural.

Thus, the final picture of the distribution of internal stresses is very complex and depends on the ratio of thermal and structural stresses in a given area of the part.

Stresses of the 3rd kind.

These are stresses that arise in the atomic lattice. We already know that in the atomic lattice, for various reasons, distortions can occur that disrupt the correct order of arrangement of atoms, for example, dislocations. A dislocation can be considered as an extra plane wedged between two adjacent planes and, as it were, pushing apart the atomic lattice in this place. Atoms located in planes adjacent to the dislocation are shifted from their normal (equilibrium) position in a given lattice. The desire of these atoms to achieve an ordered arrangement causes the appearance of internal interatomic stresses. The martensitic structure that appears in steel after hardening is characterized by a large number of dislocations. In addition, martensite has an atomic lattice in which carbon atoms are located between the iron atoms (see Fig. 9). This leads to expansion of the lattice, to its distortion, and therefore also causes internal interatomic stresses.

To summarize all that has been said, we should answer the question: are internal stresses always dangerous and undesirable? No, in some cases they are useful and help increase the strength of parts. Such a beneficial effect is exerted, for example, by compressive stresses on the surface of parts. Let's explain this. Let's imagine a dynamometer (force meter), which is stretched by two people in different directions using cables (Fig. 22). Let us assume that the dynamometer needle shows a tensile force of 50 kgf. If now two more people take hold of the cables and pull them towards the dynamometer, applying a force of 30 kgf, then the arrow on it will show 20 kgf. Internal compressive stresses formed in parts during hardening act in a similar way. For example, if tensile forces are applied to a rod, which will create a stress in it of 40 kgf/mm2, and if in this rod the internal compressive stresses obtained by hardening are equal to 15 kgf/mm2, then the stresses actually tensile on the rod will be 25 kgf/mm2. Thus, internal stresses in this case seem to unload the rod from external stress.

Why is it that internal compressive stresses at the surface are especially useful? Firstly, the maximum stresses during operation of a part almost always occur near the surface. Secondly, the most dangerous are tensile stresses, especially if there are any defects on the surface. This is clearly illustrated by the following example. Let's take a school rubber eraser for erasing and make small transverse cuts on both sides of it. Now, squeezing this eraser with two fingers from the end sides, bend it in an arc. It's easy

7. CAUSES OF DEFORMATION OF PARTS DURING HARDENING

As a result of hardening, a change in the shape and size of parts may occur. A ball bearing ring, for example, can take the shape of an oval, the axis of the roller can bend in an arc, etc. In addition, the volume of the part can change, as a result of which the exact dimensions given to it by previous machining change.

Warping is usually understood as a distortion of the shape of products, and distortion is a violation of dimensions caused by a change in volume. This interpretation, of course, is somewhat arbitrary, since any change in shape is inevitably accompanied by a change in size.

Let's consider what reasons cause warping. It can occur when products are heated. This happens if, when laid in an oven, they bend under the influence of their own weight or the mass of other parts, as well as during uneven heating in the oven, when one side of the part heats up faster than the other. For example, if cooling occurs on the side of the furnace loading window, then the surface of the part facing the window will have a lower temperature, and as a result, it will bend and warp. From this we can conclude that under proper heating conditions, warping can be minimized.

During hardening, when sudden cooling and structural transformations occur in steel, it is almost impossible to avoid warping and distortion. However, you can reduce them to minimum values. Let's see how to do this. The main reason for warping is uneven cooling of parts during hardening. This causes uneven volumetric changes, which, in turn, leads to internal stresses, and they already cause warping. This happens, for example, when hardening the rod shown in Fig. 23. No matter how quickly it is lowered into the quenching liquid, at first

The bottom side will submerge, and then the top side. At the moment when the lower part of the rod is in the cooler, and the upper part is still above its surface, volumetric compression of the lower part will occur, and the rod will bend, as shown in the figure. At a subsequent moment, when the upper part is immersed in the cooler, it will also tend to decrease in volume - to shrink and bend the rod in the other direction. However, straightening it will no longer happen, since the metal at this moment has already cooled down and therefore has lost its former ductility. Obviously, warping can be reduced if such a rod is immersed in a quenching liquid in a vertical position. 0

The change in the size of parts caused by structural transformations is relatively small in magnitude. It depends on the carbon content of the steel. An increase in carbon content by 0.1% causes an increase in volume during through hardening to martensite by only 0.1%. This means that when hardening U10 steel containing 1% C, the volume will increase by 1%. However, in the manufacture of precision products (gauges, measuring tiles) even such a small change in dimensions is unacceptable. In these cases, deformation-free hardening is sometimes used. This name, of course, is conditional, since it is almost impossible to completely avoid deformation. You can only reduce it to the desired minimum.

Rice. 23. Bending of the rod during hardening

The essence of deformation-free hardening is as follows. The part is fully machined to exact dimensions before hardening when the steel

Rice. 24. Change in shape under the influence of thermal stresses

has a pearlite structure. When heated for quenching, pearlite will turn into austenite. If after quenching it was possible to completely preserve the austenitic structure, then the volume of the part would become less than the original one, which was with a pearlite structure. If, during quenching, austenite completely transforms into martensite, then the volume will become larger than the original one. Obviously, if hardening is carried out in such a way as to obtain the amount of martensite and retained austenite in a certain ratio, then the volume of the part, and therefore its dimensions, will not change. True, it is difficult to obtain the required amount of retained austenite in carbon steel. So, for example, in U13 steel it should be 60%, and in U8 steel - 35%, which is generally unattainable. But in alloy steels, for example grade XG, this is quite feasible. Regulation of the amount of retained austenite is achieved by changing the quenching temperature and cooling rate.

Despite the fact that when hardening to martensite the volume increases, this does not mean that all dimensions of the part increase. Thus, when hardening a cylinder of great height, the diameter, especially in the middle part, decreases, and the height increases; when hardening cylinders whose height is less than the diameter, on the contrary, the height decreases, but the diameter increases; stripes and sheets increase in width, and sometimes decrease in length; the rings increase in width and thickness, and decrease in diameter.

Thermal stresses tend to change the shape of the product so that it approaches the shape of a ball.

For example, in a cube-shaped part, as a result of thermal stresses, the edges become convex (Fig. 24,a), the cylinder shortens in length and increases in diameter (Fig. 24,6). As a result, the overall picture of deformations becomes so complicated that in many cases it is not possible to foresee in advance all possible changes in the dimensions of a part after hardening, and the issue is resolved experimentally.

Technical calculations for heat treatment

When performing calculations, the required amount of technological equipment is determined. Calculations also come down to a technically sound calculation of the consumption of various types of technological energy (electricity, gas, water, steam, air spent on the technological needs of production).

Calculation of electricity consumption

The main consumers of electricity in thermal shops are electric furnaces, heating units and electric motors used for pushers and conveyors of furnaces, conveyors of quenching tanks, pumps of oil cooling units, washing machines, air ducts, fans, etc. The required amount of electricity for electric furnaces is calculated based on their power and the number of hours of operation, taking into account the furnace power utilization factor and the load factor, and for other equipment - only the load factor:

E = Nnф0 K3hn

, J (kWh),

where E

— annual electricity consumption, J (kWh);
N
—furnace power, kW;
n
is the number of equipment units;
Фo — actual annual equipment time fund, h; K
3 - equipment load factor; hн is the efficiency factor of the furnace in terms of power.

After all consumers have been identified, a list of required electricity for the year is compiled. Calculation of electricity consumption for lighting is carried out taking into account the area of the site (workshop) and the coefficient of simultaneous burning of lamps:

kW,

where h

0—simultaneous combustion coefficient (
h0
=0.8);
g
—specific energy consumption for lighting (
g
= 11 W/m2);
T
is the number of hours of combustion
;
F is the area of the site (workshop), m2.

Calculation of gas consumption for technological needs

This calculation is carried out on the basis of the heat balance of the furnace or according to the actual standards of a given enterprise. The calculated average annual gas consumption (m3/h) is multiplied by the required number of hours of operation of the furnace, and thus the annual gas consumption is obtained:

g
= N
Fd
N
, m3,

where N

-number of ovens;
Fd is the actual time of the furnace, h; N
— hourly gas consumption, m3/h.

Calculation of high pressure air flow (5…6

atm
)
The calculation is made based on the following standards: in hardening presses and machines 0.4...0.5 m3/h; in the lifts of furnace dampers, etc. - 0.5...0.7 m3/h; in shot blasting machines 2…5 m3/min.

Calculation of water requirements for production needs

The calculation is made based on the established standards for processing operations and for household needs based on the number of employees:

— for hardening: 6...8 m3/t of processed products;

— for cooling coils in oil tanks: 10...12 m3/t;

— for washed processed products: 20...30% by weight of washed products;

— for cooling in water after tempering: 2...4% of the mass of released products;

— for cooling inductor lamps and for hardening at high-frequency installations: 2...8 m3/h.

Calculation of steam consumed for heating solutions in washing machines,

rinsing tanks, etc.

The calculation is carried out based on the following conditional norms:

— for heating solutions in washing machines and rinsing tanks: 15% by weight of the products being washed;

— for heating pickling and neutralization baths: 15...20% by weight of processed products.

Calculations of the required amount of various types of technological energy are completed by drawing up a summary statement.

Calculations of auxiliary materials

These calculations (quenching oil, carburizer, caustic soda, soda ash and others) for technological needs are carried out according to specific consumption rates and are completed by drawing up a summary statement.

Examples of technical calculations

Example 1.

Calculate the duty of the chamber furnace (required operating time) for hardening the cutting tool.
The annual program is Q
=2800 pcs.
or 16800 kg. Number of products in the cage according to the technological map n
c = 8 pcs.
or the weight of the cage is 48 kg. The number of cages ( M
) in the annual program will be
M=Q/n
c=2800:8 or 16800:48 = 3500 cages.

The normalized time for processing one cage is taken equal to T

c = 60 min, then the normalized time for the annual production volume for this product item will be = 3500 hours.

Consequently, the required operating time (O) of the chamber furnace equipment for tool hardening to complete the annual program will be 3500 furnace hours.

The received data is entered into the loading list.

When calculating equipment debt by specific (shop) productivity, it is necessary to know the productivity of the furnace. For a chamber furnace brand SNZ.3.0×6.5×2.0/10 (N-15) the productivity is R

=50 kg/h.
Then the required operating time (P3) of the chamber furnace for hardening the tool to complete the annual production is P3 = Q/P
= 16800/50 = 3360 furnace hours.

Example 2.

Calculate the number of chamber furnaces CP3.3.0×6.5×2.0/10 (N-15) for tool hardening. The calculation is made based on the required operating time and the actual annual operating time of the equipment:

Nр = П

3
/
F
.
The actual annual operating time of equipment is calculated using the formula

Фд= [(365- А-В) а m

]
Kr
oven-hours,

where 365 is the calendar annual time fund in days;

— the number of days off per year is 52;

- number of holidays per year - 8;

— number of hours of work per shift — 8;

— number of shifts — 1;

– coefficient of time loss for repairs, readjustment of modes and heating of the furnace (taken within 6...10%, i.e. Kr = 0.94...0.90).

Fd = [(365-52-8)8∙1]0.94 = 2294 hours,

then Nр =

P3
/
F = 3500/2294 = 1.52 pcs.

We accept the number of ovens N

pr = 2 pcs.

Determine the furnace load factor: K

з
=Nр/N
pr∙100=1.52/2.0 = 76%.

The obtained data is entered into a summary list of equipment composition.

Reference data is presented in tables.

Examples of technological equipment calculations

Example 1.

Calculate the required number of technological installations for laser hardening of a shaft made of ShKh15 steel (Fig. 45) to a hardness of 58...60
HRC
.
Annual production program: 20,000 pcs. Hardening modes: P
= 800 W,
d
= 4 mm, n = 4 mm/s, tracks are applied in a ring along the entire length of the shaft, overlap coefficient Kp = 1.5.

Rice. 45. Scheme of laser heat strengthening ("ring" scheme) of a shaft made of ShKh15 steel

Calculation of electricity consumption

E = Nnф0 K3hn

, J (kWh),

where E

kW,

where h

0—simultaneous combustion coefficient (
h0
=0.8);
g
—specific energy consumption for lighting (
g
= 11 W/m2);
T
is the number of hours of combustion
;
F is the area of the site (workshop), m2.

Calculation of gas consumption for technological needs

g
= N
Fd
N
, m3,

where N

-number of ovens;
Fd is the actual time of the furnace, h; N
— hourly gas consumption, m3/h.

Calculation of high pressure air flow (5…6

Calculation of water requirements for production needs

The calculation is made based on the established standards for processing operations and for household needs based on the number of employees:

— for hardening: 6...8 m3/t of processed products;

— for cooling coils in oil tanks: 10...12 m3/t;

— for washed processed products: 20...30% by weight of washed products;

— for cooling in water after tempering: 2...4% of the mass of released products;

— for cooling inductor lamps and for hardening at high-frequency installations: 2...8 m3/h.

Calculation of steam consumed for heating solutions in washing machines,

rinsing tanks, etc.

The calculation is carried out based on the following conditional norms:

— for heating solutions in washing machines and rinsing tanks: 15% by weight of the products being washed;

— for heating pickling and neutralization baths: 15...20% by weight of processed products.

Calculations of the required amount of various types of technological energy are completed by drawing up a summary statement.

Calculations of auxiliary materials

Examples of technical calculations

Example 1.

The normalized time for processing one cage is taken equal to T

c = 60 min, then the normalized time for the annual production volume for this product item will be = 3500 hours.

Consequently, the required operating time (O) of the chamber furnace equipment for tool hardening to complete the annual program will be 3500 furnace hours.

The received data is entered into the loading list.

When calculating equipment debt by specific (shop) productivity, it is necessary to know the productivity of the furnace. For a chamber furnace brand SNZ.3.0×6.5×2.0/10 (N-15) the productivity is R

=50 kg/h.
Then the required operating time (P3) of the chamber furnace for hardening the tool to complete the annual production is P3 = Q/P
= 16800/50 = 3360 furnace hours.

Example 2.

Nр = П

3
/
F
.
The actual annual operating time of equipment is calculated using the formula

Фд= [(365- А-В) а m

]
Kr
oven-hours,

where 365 is the calendar annual time fund in days;

— the number of days off per year is 52;

- number of holidays per year - 8;

— number of hours of work per shift — 8;

— number of shifts — 1;

– coefficient of time loss for repairs, readjustment of modes and heating of the furnace (taken within 6...10%, i.e. Kr = 0.94...0.90).

Fd = [(365-52-8)8∙1]0.94 = 2294 hours,