Tensile strength
- this is the same as the temporary resistance of the material.
But despite the fact that it is more correct to use the term temporary resistance
, the concept of tensile strength has taken root better in technical colloquial speech.
At the same time, in regulatory documentation and standards the term “temporary resistance” is used. ©ICM(www.modificator.ru)
Strength
- this is the resistance of a material to deformation and destruction, one of the main
mechanical properties
. In other words, strength is the ability of materials to withstand certain influences (loads, temperature, magnetic and other fields) without collapsing.
To the tensile strength characteristics
include normal modulus of elasticity, proportional limit, elastic limit, yield strength and tensile strength (tensile strength).
Tensile strength
— this is the maximum mechanical stress above which destruction of the material subject to deformation occurs; tensile strength is designated σB and is measured in kilograms of force per square centimeter (kgf/cm2), and is also indicated in megapascals (MPa).
There are:
- tensile strength,
- compressive strength,
- bending strength,
- torsional strength.
Short-term strength (MPa)
determined using tensile tests, deformation is carried out until failure. Tensile tests are used to determine tensile strength, elongation, elastic limit, etc. Long-term strength tests are intended primarily to assess the possibility of using materials at high temperatures (long-term strength, creep); as a result, σB/Zeit is determined - the limit of limited long-term strength for a given service life. [1]
©ICM (www.modificator.ru)
Physics of strength
founded by Galileo: summarizing his experiments, he discovered (1638) that in tension or compression, the fracture load
P
for
a given material depends only on the cross-sectional area
F. This is how a new physical quantity appeared - stress σ=P
/
F
- and a physical constant of the material: fracture stress [4].
Physics of fracture as a fundamental science of the strength of metals
arose in the late 40s of the XX century [5]; this was dictated by the urgent need to develop scientifically based measures to prevent the increasingly frequent catastrophic destruction of machines and structures. Previously, in the field of strength and destruction of products, only classical mechanics was taken into account, based on the postulates of a homogeneous elastic-plastic solid body, without taking into account the internal structure of the metal. The physics of destruction also takes into account the atomic-crystalline structure of the metal lattice, the presence of defects in the metal lattice and the laws of interaction of these defects with elements of the internal structure of the metal: grain boundaries, second phase, non-metallic inclusions, etc.
Great influence on the strength of the material
is influenced by the presence of surfactants in the environment that can be strongly adsorbed (moisture, impurities); the tensile strength decreases.
Increasing the strength of a metal is caused by targeted changes in the metal structure, including modification of the alloy.
Educational film about the strength of metals (USSR, year of release: ~1980):
Tensile strength values [edit | edit code ]
Static tensile strength [edit | edit code ]
Static tensile strength, also often called simply tensile strength, is a threshold value of constant mechanical stress, exceeding which constant mechanical stress will destroy a certain body made of a particular material. According to GOST 1497-84 “Methods of tensile testing”, a more correct term is temporary fracture strength
- stress corresponding to the greatest force preceding the rupture of the sample during (static) mechanical tests. The term comes from the idea that a material can withstand any static load indefinitely if it creates stresses less than the static tensile strength, that is, not exceeding the temporary resistance. Under a load corresponding to the temporary resistance (or even exceeding it - in real and quasi-static tests), the material will collapse (the test sample will be crushed into several parts) after a finite period of time (possibly almost immediately - that is, no longer in less than 10 s).
Dynamic tensile strength [edit | edit code ]
The dynamic tensile strength is the threshold value of alternating mechanical stress (for example, during impact), exceeding which the alternating mechanical stress will destroy a body made of a particular material. In the case of dynamic impact on this body, the time of its loading often does not exceed several seconds from the beginning of loading to the moment of destruction. In such a situation, the corresponding characteristic is also called conditionally instantaneous tensile strength
, or
brittle-short-term tensile strength
.
Compressive strength [edit | edit code ]
Compressive strength is a threshold value of constant (for static tensile strength) or, accordingly, variable (for dynamic tensile strength) mechanical stress, exceeding which the mechanical stress will result (in a finite, fairly short period of time) compressing a body made of a specific material - the body will collapse or becomes unacceptably deformed.
Tensile-compressive stresses
Static tensile strength condition
The longitudinal force N, determined by the section method, is the resultant of the internal forces distributed over the cross section of the rod (Fig. 2, b). Based on the definition of stress, according to expression (1), we can write for the longitudinal force:
where σ is the normal stress at an arbitrary point in the cross section of the rod. To determine normal stresses at any point of a beam, it is necessary to know the law of their distribution over the cross section of the beam. Experimental studies show: if a series of mutually perpendicular lines are applied to the surface of the rod, then after applying an external tensile load the transverse lines do not bend and remain parallel to each other (Fig. 6, a). This phenomenon is evidenced by the hypothesis of plane sections (Bernoulli's hypothesis): sections that are flat before deformation remain flat after deformation.
Since all the longitudinal fibers of the rod are deformed equally, the stresses in the cross section are the same, and the stress diagram σ along the height of the cross section of the rod looks as shown in Fig. 6, b. It can be seen that the stresses are uniformly distributed over the cross section of the rod, i.e. at all points of the section σ = const. The expression for determining the voltage value has the form:
Thus, the normal stresses arising in the cross sections of a tensile or compressed beam are equal to the ratio of the longitudinal force to the area of its cross section. Normal stresses are considered to be positive in tension and negative in compression.
Strength characteristics of some materials [edit | edit code ]
The values of the ultimate stress (ultimate strength) for tension and compression for many materials usually differ.
Composites typically have a tensile strength greater than their compressive strength. For ceramics (and other brittle materials), on the contrary, it is typical that the compressive strength exceeds the tensile strength many times over. For metals, metal alloys, and many plastics, as a rule, the compressive strength is equal to the tensile strength. To a greater extent, this is due not to the physics of materials, but to the characteristics of loading, stress state patterns during testing, and the possibility of plastic deformation before failure.
The strength of solids is ultimately determined by the forces of interaction between the atoms that make up the body. As the distance between atoms increases, they begin to attract, and at the critical distance the force of attraction is maximum in absolute value. The stress corresponding to this force is called the theoretical tensile strength and is σtheor ≈ 0.1E, where E is Young's modulus. However, in practice, destruction of materials is observed much earlier, this is explained by inhomogeneities in the structure of the body, due to which the load is distributed unevenly.
Some values of tensile strength σ 0 <0>> in MPa (1 kgf/mm² = 100 kgf/cm² ≈ 10 MN/m² = 10 MPa) (1 MPa = 1 N/mm² ≈ 10 kgf/cm²) [1]:
The strength of metal structures is one of the most important parameters that determine their reliability and safety. Since ancient times, issues of strength were solved experimentally - if any product broke, then the next one was made thicker and more massive. Since the 17th century, scientists began a systematic study of the problem; the strength parameters of materials and structures made from them can be calculated in advance, at the design stage. Metallurgists have developed additives that affect the strength of steel alloys.
Definition
The tensile strength of a material is an intensive property; therefore its value is independent of the size of the test sample. However, depending on the material, this may depend on other factors such as sample preparation, the presence or absence of surface defects, and the temperature of the environment and the material being tested.
Some materials break very abruptly without what is called brittle fracture. Others, which are more ductile, including most metals, experience some plastic deformation and possibly contraction before fracture.
Tensile strength is defined as stress, which is measured as force per unit area. For some heterogeneous materials (or for assembled components) this may be expressed as a force or as a force per unit width. In the International System of Units (SI), the unit of measurement is the pascal (Pa) (or its multiple, often megapascals (MPa), using the SI prefix mega
); or, equivalent to pascals, newtons per square meter (N/m2). A common unit of measurement in the United States is pounds per square inch (psi or psi). Kilofunds per square inch (ksi, or sometimes kpsi) is equal to 1000 psi and is commonly used in the United States when measuring tensile strength.
Plastic materials
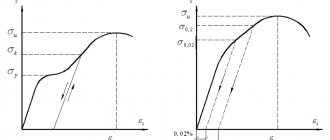
Figure 1: “Engineering” stress-strain curve (σ – ε) typical for aluminum 1. Ultimate Strength 2. Yield Strength 3. Proportional Ultimate Stress 4. Fracture 5. Displacement Strain (typically 0.2%)
Figure 2: "Technical" (red) and "true" (blue) stress-strain curve typical of structural steel.
- 1: Absolute Strength
- 2: Yield strength (yield strength)
- 3: Break
- 4: Strain hardening region
- 5: neck area
- A: Apparent voltage ( F
/
A
) - B: Actual voltage ( F
/
A
)
Many materials can exhibit linear elastic behavior, defined by a linear stress-strain relationship, as shown in Figure 1 up to point 3. The elastic behavior of materials often extends into the nonlinear region, represented in Figure 1 by point 2 (the "yield limit"), up to which the deformation is completely are restored when the load is removed; that is, a specimen loaded elastically in tension elongates, but when unloaded returns to its original shape and size. Outside this elastic region, for ductile materials such as steel, deformations are ductile. A plastically deformed sample does not return completely to its original size and shape when unloaded. For many applications, plastic deformation is not acceptable and is used as a design constraint.
After yield stress, ductile metals go through a period of strain hardening in which stress increases again with increasing strain, and they begin to taper as the cross-sectional area of the specimen decreases due to plastic flow. In a sufficiently ductile material, when necking becomes significant, it causes a change in the engineering stress-strain curve (curve A, Figure 2); this is due to the fact that the engineering stress
calculated from the original cross-sectional area before necking. The turning point is the maximum stress on the engineering stress-strain curve, and the engineering stress coordinate of this point is the tensile strength determined by point 1.
Tensile strength is not used in the design of ductile static members because design methods dictate the use of yield strength. However, it is used for quality control due to ease of testing. It is also used to approximate material types for unknown samples.
Tensile strength is a common engineering parameter when designing brittle material members, since such materials do not have a yield strength.
How is strength testing performed?
Strength tests for tensile strength are carried out on special test benches. One end of the test sample is fixedly fixed in them, and a drive mount, electromechanical or hydraulic, is attached to the other. This drive creates a smoothly increasing force that acts to break the sample, or to bend or twist it.
Tensile test
The electronic control system records the tensile force and relative elongation, and other types of deformation of the sample.
Elongation (at break)
Often called "relative elongation". An increase in the distance between two marks on a test specimen that occurs as a result of the specimen deforming under tension until it breaks between the marks.
The amount of elongation depends on the cross-sectional dimensions of the sample. For example, the amount of elongation that is obtained when testing an aluminum sheet specimen will be lower for a thin sheet than for a thick sheet. The same applies to extruded aluminum profiles.
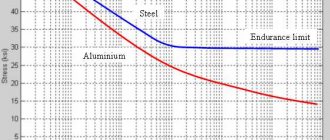
Figure 5 – Influence of alloying elements on strength properties and elongation
Extension A
Percentage elongation after specimen rupture at an initial distance between marks of 5.65 · √ S, where S is the initial cross-sectional area of the test specimen. The outdated designation of this quantity A5 is currently not used. A similar value in Russian-language documents is designated δ5.
It is easy to check that for round samples this distance between the original marks is calculated as 5·d.
Extension A50mm
The percentage elongation after specimen rupture, relative to the original length between the 50 mm marks and the constant original width of the test specimen (typically 12.5 mm). In the USA, a distance between marks of 2 inches is used, that is, 50.8 mm.
Types of tensile strength
Tensile strength is one of the main mechanical parameters of steel, as well as any other structural material.
This value is used in strength calculations of parts and structures; based on it, it is decided whether a given material is applicable in a particular area or whether a more durable one needs to be selected.
The following types of tensile strength are distinguished:
- compression - determines the ability of a material to resist the pressure of an external force;
- bending - affects the flexibility of parts;
- torsion - shows how suitable the material is for loaded drive shafts that transmit torque;
- stretching
Types of material strength tests
The scientific name for the parameter used in standards and other official documents is tensile strength.
Parameter classification
The material has temporary resistance in response to impacts of various types, so the characteristic is classified into several groups. Forces to which the workpiece or structural element is subjected:
- Stretching. The product is pulled by the edges using a special machine.
- Torsion. The object is placed in conditions under which the rotating shaft operates.
- Bend. The workpiece is bent and unbent in several directions.
- Compression. The material is pressed alternately from different sides.
For the same material, the PP may vary. An example is steel. It is used more often than other alloys because steel structures have proven to be the strongest, most durable, and most resistant to the elements. At the same time, they are reliable and do not emit harmful substances into the atmosphere.
There are several grades of steel. They are produced using different technologies, and depending on this, the characteristics of the workpieces and structures differ. For conventional brands, the PP is 300 MPa. As the carbon content increases, the strength increases. The hardest grades have a value of 900 MPa. Factors on which strength characteristics depend:
- the amount of useful and undesirable impurities;
- method of heat treatment (cryotreatment, hardening, annealing).
Tensile strength of steel
Today, steel is still the most used structural material, gradually losing its position to various plastics and composite materials. Its durability, reliability and safety in operation depend on the correct calculation of the strength limits of a metal.
The tensile strength of steel depends on its grade and varies from 300 MPa for ordinary low-carbon structural steel to 900 MPa for special high-alloy grades.
The parameter value is affected by:
- chemical composition of the alloy;
- thermal procedures that help strengthen materials: hardening, tempering, annealing, etc.
Some impurities reduce strength, and they try to get rid of them at the casting and rolling stage, while others, on the contrary, increase it. They are specially added to the alloy composition.
Proof of Yield
In addition to the tensile strength, the related concept of yield strength, denoted σt, is widely used in engineering calculations. It is equal to the amount of tensile strength that must be created in the material in order for the deformation to continue to increase without increasing the load. This state of the material immediately precedes its destruction.
At the microlevel, at such stresses, interatomic bonds in the crystal lattice begin to break, and the specific load on the remaining bonds increases.
General information and characteristics of steels
From the designer’s point of view, the physical and mechanical parameters of steel are of greatest importance for alloys operating under normal conditions. In some cases, when the product is to operate under conditions of extremely high or low temperatures, high pressure, high humidity, or under the influence of aggressive environments, the chemical properties of steel become equally important. Both the physical-mechanical and chemical properties of alloys are largely determined by their chemical composition.
Alloying additives in alloys
These are substances deliberately added to the melt to improve the properties of the alloy and bring its parameters to the required ones. Some of them are added in large quantities (more than a percent), others in very small quantities. I most often use the following alloying additives:
- Chromium. Used to increase hardenability and hardness. Share – 0.8-0.2%.
- Bor. Improves cold brittleness and radiation resistance. Share – 0.003%.
- Titanium. Added to improve the structure of Cr-Mn alloys. Share – 0.1%.
- Molybdenum. Increases strength characteristics and corrosion resistance, reduces fragility. Share – 0.15-0.45%.
- Vanadium. Improves strength parameters and elasticity. Share – 0.1-0.3%.
- Nickel. Promotes an increase in strength characteristics and hardenability, but at the same time leads to an increase in fragility. This effect is compensated by the simultaneous addition of molybdenum.
Metallurgists also use more complex combinations of alloying additives, achieving unique combinations of physical and mechanical properties of steel. The cost of such grades is several times (or even tens of times) higher than the cost of conventional low-carbon steels. They are used for particularly critical structures and assemblies.
If you find an error, please select a piece of text and press Ctrl+Enter.
Using the properties of metals
Two important indicators - plasticity and PP - are interrelated. Materials with a large first parameter degrade much more slowly. They change their shape well and are subjected to various types of metal processing, including die stamping - that’s why car body elements are made from sheets. With low ductility, alloys are called brittle. They can be very hard, but at the same time have poor stretching, bending and deformation, for example, titanium.
Resistance
There are two types:
- Regulatory - prescribed for each type of steel in GOSTs.
- Calculated - obtained after calculations in a specific project.
The first option is rather theoretical; the second is used for practical tasks.