Чему равен коэффициент упругости?

Главная
Справочник
Физика

При воздействии внешних сил тела способны приобретать ускорения или деформироваться. Деформацией называют изменение размеров и (или) формы тела. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.
Пусть на пружину на рис.1 действует растягивающая сила, направленная вертикально вниз.

При воздействии деформирующей силы ($\overline{F}$) длина пружины увеличивается. В пружине возникает сила упругости (${\overline{F}}_u$), которая уравновешивает деформирующую силу. Если деформация небольшая и упругая, то удлинение пружины ($\Delta l$) пропорционально деформирующей силе:

\[\overline{F}=k\Delta l\left(1\right),\]

где в качестве коэффициента пропорциональности выступает жесткость пружины $k$. Коэффициент $k$ называют также коэффициентом упругости, коэффициентом жесткости. Жесткость (как свойство) характеризует упругие свойства тела, подвергаемого деформации — это возможность тела оказывать противодействие внешней силе, сохранять свои геометрические параметры. Коэффициент жесткости является основной характеристикой жесткости.

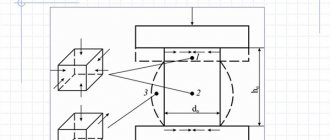
Коэффициент жесткости пружины зависит от материала, из которого изготовлена пружина, ее геометрических характеристик. Так, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси вычисляется при помощи формулы:

\[k=\frac{Gd^4}{8d^3_pn}\left(2\right),\]

где $G$ -модуль сдвига (величина зависящая от материала); $d$ — диаметр проволоки; $d_p$ — диаметр витка пружины; $n$ — количество витков пружины.

Чему равен коэффициент жесткости стержня если под действием силы 1000?

Ответ: жесткость стержня

составляет k = 1 *10^6 Н/м.

Интересные материалы:

Можно ли использовать фольгу для запекания в мультиварке? Можно ли использовать обычную посуду для индукционной плиты? Можно ли использовать обычную сковороду на индукционной плите? Можно ли использовать силиконовые формы для выпечки в газовой печи? Можно ли использовать сковороду для индукционных плит на газовой плите? Можно ли использовать сковороду с антипригарным покрытием в духовке? Можно ли использовать сверла по металлу на дереве? Можно ли использовать в духовке посуду для микроволновки? Можно ли каменную сковородку в духовку? Можно ли кастрюли для индукции использовать на газу?

Удельные показатели жесткости

При сравнении жесткости, прочности и массы деталей, изготовленных из различных материалов, следует различать четыре основных случая.

1. Детали одинаковы по конфигурации (при равной нагрузке имеют одинаковые напряжения).

2. Детали равножестки (имеют одинаковые деформации при различных сечениях и напряжениях).

3. Детали равнопрочны (имеют одинаковый запас прочности, различные сечения и напряжения, пропорциональные пределу прочности материала).

4. Детали имеют одинаковую массу.

Первый случай (замена материала детали другим без изменения ее геометрических размеров) практически встречается, когда сечения детали заданы технологическим процессом (например, литые корпусные детали). Это также случай нерасчетных деталей с неопределенными напряжениями. Второй и третий случай имеют место при замене материала детали другим с одновременным изменением ее сечений (расчетные детали, в которых напряжения и деформации определяются достаточно точно и назначаются с расчетом максимального использования прочности и жесткости материала). Четвертый случай — это случай, когда масса конструкции задана ее функциональным назначением и условиями эксплуатации.

При сравнении прочностных, массовых и жесткостных показателей деталей, изготовленных из различных материалов, будем предполагать, что длина деталей одинакова, а сечения в последних трех случаях изменяются геометрически подобно.

1. Детали одинаковой конфигурации (σ = const). В случае растяжения-сжатия относительный коэффициент жесткости согласно формуле () λ’ = EF, где F — сечение детали; Е — модуль нормальной упругости.

По условию F = const. Следовательно, λ = const Е, т. е. жесткость деталей в данном случае зависит только от модуля упругости.

Запас прочности n = σв/σ, где σв — предел прочности на растяжение; σ — действующее в детали напряжение.

По условию σ = const. Следовательно, и n = const σв.

Масса детали m = γFI = const γ, где γ — плотность материала.

Совершенно аналогичны соотношения в случае изгиба и кручения, с той лишь разницей, что при кручении жесткость детали определяется модулем сдвига.

2. Равножесткие детали (λ = const). Условие равножесткости в случае растяжения-сжатия согласно формуле ()

Следовательно,

Масса равножестких деталей

Напряжения

С учетом формулы (52) σ = const Е. Запас прочности

При изгибе масса равножестких деталей

Запас прочности

3. Равнопрочные детали (n = const). Условие равнопрочности при растяжении-сжатии

Ввиду того, что σ = const/F, n = const σвF = const. Следовательно, для равнопрочных деталей

и масса

Коэффициент жесткости с учетом формулы (53)

При изгибе

4. Детали равной массы (m = const). Условие равной массы при растяжении-сжатии m = γFl = const.

Следовательно, F = 1/γ.

Напряжения

Запас прочности

Коэффициент жесткости

При изгибе

Для сравнительных целей пользуются наиболее простыми формулами для растяжения- сжатия.

Показатели массы, жесткости и прочности при растяжении-сжатии для всех разобранных выше случаев приведены в табл. 19.

Значения удельной прочности n/m = σ0,2/γ и удельной жесткости λ/m = Е/γ одинаковы для всех категорий деталей.

Как видно из табл. , величина Е/γ для большинства материалов одинакова (Е/γ ≈ 25·106). Исключение представляют чугуны серые (Е/γ = 11·106) и высокопрочные (Е/γ = 21·106).

С учетом данных табл. 19 и составлены графики показателей жесткости, прочности и массы деталей, изготовленных из различных материалов (рис. 93).

В случае деталей одинаковой конфигурации (рис. 93, a) по жесткости Е и прочности σ0,2 наиболее выгодны стали и сплавы Ti, а по массе γ — сплавы Аl и Mg.

Так как модуль упругости сплавов определяется модулем упругости основного компонента и мало зависит от содержания (в обычных количествах) легирующих элементов (например, для сталей колебания заключены в пределах E = (19—22)·104 МПа, для сплавов Аl в пределах E =(7,0—7,5)·104 МПа), то в случае деталей одинаковой конфигурации, когда на первом плане стоят требования жесткости, а уровень напряжений невысок, целесообразно применять наиболее дешевые материалы (углеродистые стали вместо легированных, алюминиевые сплавы простого состава вместо легированных). Если же наряду с жесткостью имеет значение прочность, то предпочтительны прочные сплавы.

Для деталей равной жесткости (рис. 93, б) по прочности (σ0,2/Е) наиболее выгодны сверхпрочные стали и сплавы Ti. Масса равножестких деталей одинакова (за исключением деталей из серых чугунов).

В случае равнопрочных деталей (рис. 93, в) наименьшей массой и наиболее низкой жесткостью обладают сверхпрочные и легированные стали, СВАМ и сплавы Ti. Наиболее жесткие детали из углеродистых сталей, литых сплавов Аl и Mg и серых чугунов, т. е. наименее прочных материалов.

Это справедливо только при условии равнопрочности (расчетные напряжения пропорциональны пределу прочности). Жесткость деталей, выполненных из прочных материалов, можно повысить снижением расчетных напряжений, но в ущерб массе конструкции и с недоиспользованием их прочностного ресурса. Практический вывод заключается в том, что при использовании прочных материалов в равнопрочных конструкциях необходимо считаться с уменьшением жесткости и компенсировать ее снижение конструктивными мерами.

В случае деталей равной массы (рис. 93, г) прочность пропорциональна фактору σ0,2/γ. Жесткость одинакова (за исключением деталей из серых чугунов, обладающих пониженной жесткостью).

Сравним жесткость, прочность и массу деталей, выполненных из углеродистых, легированных сталей и сплавов Al, Mg и Ti (табл. 20). Характеристики деталей из углеродистых сталей приняты равными единице.

Для деталей одинаковой конфигурации переход с углеродистой стали на литейные сплавы Аl и Mg вызывает уменьшение жесткости, прочности и массы. При переходе на серые чугуны жесткость снижается в 2,5, а прочность в 2 раза. Масса практически не изменяется.

Для деталей равной жесткости переход с углеродистой стали на деформируемые сплавы Аl, легированные стали и сплавы Ti сопровождается увеличением прочности соответственно в 2,5; 3,3 и 5 раз. Масса деталей не изменяется.

Для равнопрочных деталей переход на сплавы Аl, легированные стали и сплавы Ti вызывает снижение жесткости и массы соответственно в 2,5; 3 и 5 раз.

Для деталей равной массы переход на сплавы Аl, легированные стали и сплавы Ti сопровождается увеличением прочности соответственно в 2,5; 3 и 5 раз. Жесткость не изменяется.

Обобщенный показатель. Как видно из табл. 19, прочность для всех категорий деталей определяется фактором σ0,2/γ, а жесткость — фактором Е/γ.

Обобщенный показатель, представляющий собой произведение σ0,2E/γ2 этих факторов, характеризует способность материалов нести наиболее высокие нагрузки при наименьших деформациях и массе и наиболее полно оценивает выгодность по массе материалов.

Прочность и жесткость практически неотделимы. Жесткость сама по себе не представляет ценности, если конструкция не может нести высоких нагрузок. Низкоуглеродистая сталь имеет такой же модуль упругости, как и термообработанная качественная сталь. Однако деталь из углеродистой стали пластически деформируется и выйдет из строя под действием небольших нагрузок, которые вызовут во второй детали лишь незначительные упругие деформации.

Выгодность материалов с Е/γ = const ≈ 25·106 (см. табл. ) вполне характеризуется фактором σ0,2/γ, который в этом случае является универсальным прочностно-жесткостным показателем. Для материалов с иным значением Е/γ фактор σ0,2/γ должен быть исправлен на отношение их удельной жесткости к Е/γ = 25·106, например, для чугунов; серых — на 11/25 = 0,44, высокопрочных — на 21/25 = 0,85.

Значения обобщенного показателя σ0,2E/γ2 приведены в табл. и на рис. 94.

На практике выбор материала определяется не только прочностно-жесткостными характеристиками, но и другими свойствами (технологическими). Поэтому преимущественное значение имеют конструктивные меры, позволяющие создать достаточно прочные и жесткие конструкции даже при использовании материалов малой прочности и жесткости.

Потенциальная энергия сжатой или растянутой пружины

Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину $\Delta L $ обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией

Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).

Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:

\[ \large \boxed{ E_{p} = \frac{k}{2} \cdot \left( \Delta L \right)^{2} }\]

$ E_{p} \left( \text{Дж} \right)$ – потенциальная энергия сжатой или растянутой пружины;

$ \Delta L \left(\text{м} \right) $ – удлинение пружины;

$ \displaystyle k \left(\frac{H}{\text{м}} \right) $ – коэффициент жесткости (упругости) пружины.

Выводы

Упругие тела – такие, которые сопротивляются деформации;
Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
Деформация – изменение формы, или размеров тела;
Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
Удлинение пружины – это разность ее конечной и начальной длин;
Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.

Растяжение пружины

Рассмотрим подробнее деформацию растяжения на примере пружины.

Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина $L_{0}$ пружины.

Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение

Подвесим теперь к пружине груз. Пружина будет иметь длину $L$, указанную на рисунке справа.

Сравним длину нагруженной пружины с длиной свободно висящей пружины.

\[ \large L_{0} + \Delta L = L \]

Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину $L_{0}$.

\[ \large \boxed{ \Delta L = L — L_{0} }\]

$ L_{0} \left(\text{м} \right) $ – начальная длина пружины;

$ L \left(\text{м} \right) $ – конечная длина растянутой пружины;

$ \Delta L \left(\text{м} \right) $ – кусочек длины, на который растянули пружину;

Величину $ \Delta L $ называют удлинением пружины.

Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.

Примечание: Отношение – это дробь. Относительное – значит, дробное.

\[ \large \boxed{ \frac{\Delta L }{ L_{0}} = \frac{ L — L_{0}}{L_{0} } = \varepsilon } \]

$ \varepsilon $ – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.

Соединяем две одинаковые пружины

В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.

Параллельное соединение пружин

На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину $\Delta L$. Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины

Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом $mg$.

Одна пружина:

\[ \large k_{1} \cdot \Delta L = m \cdot g \]

Две параллельные пружины:

\[ \large k_{\text{параллел}} \cdot \Delta L \cdot \frac{1}{2}= m \cdot g \]

Так как правые части уравнений совпадают, левые части тоже будут равны:

\[ \large k_{\text{параллел}} \cdot \Delta L \cdot \frac{1}{2}= k_{1} \cdot \Delta L \]

Обе части уравнения содержат величину $\Delta L $. Разделим обе части уравнения на нее:

\[ \large k_{\text{параллел}} \cdot \frac{1}{2}= k_{1} \]

Умножим обе части полученного уравнения на число 2:

\[ \large \boxed{ k_{\text{параллел}} = 2k_{1} } \]

Коэффициент жесткости $k_{\text{параллел}}$ двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной

Последовательное соединение пружин

Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину $\Delta L$. Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.

Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.

На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину $\Delta L$.

Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины

Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом $mg$.

Одна пружина:

\[ \large k_{1} \cdot \Delta L = m \cdot g \]

Две последовательные пружины:

\[ \large k_{\text{послед}} \cdot \Delta L \cdot 2 = m \cdot g \]

Так как правые части уравнений совпадают, левые части тоже будут равны:

\[ \large k_{\text{послед}} \cdot \Delta L \cdot 2 = k_{1} \cdot \Delta L \]

Обе части уравнения содержат величину $\Delta L $. Разделим обе части уравнения на нее:

\[ \large k_{\text{послед}} \cdot 2 = k_{1} \]

Разделим обе части полученного уравнения на число 2:

\[ \large \boxed{ k_{\text{послед}} = \frac{k_{1}}{2} } \]