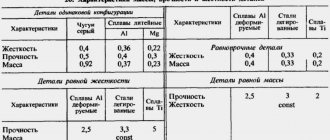
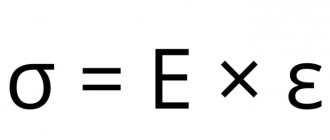Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.
Основные сведения
Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м 2 или в Па.
Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (10 12 Па)
Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.
Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.
График теста на растяжение
E- это частное от деления нормальных напряжений σ на относительное удлинение ε.
Закон Гука также можно сформулировать и с использованием модуля Юнга.
Диаграмма растяжения
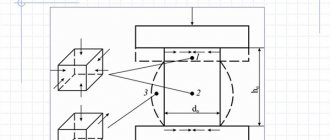
Для исследования деформации растяжения стержень из исследуемого материала при помощи специальных устройств (например, с помощью гидравлического пресса) подвергают растяжению и измеряют удлинение образца и возникающее в нем напряжение. По результатам опытов вычерчивают график зависимости напряжения σ
от относительного удлиненияε
. Этот график называют диаграммой растяжения (рис. 10).
Рис. 10
Многочисленные опыты показывают, что при малых деформациях напряжение σ
прямо пропорционально относительному удлинениюε
(участок
ОА
диаграммы) – выполняется закон Гука.
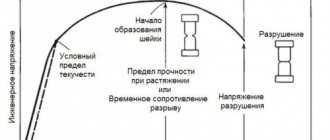
Эксперимент показывает, что малые деформации полностью исчезают после снятия нагрузки (наблюдается упругая деформация). При малых деформациях выполняется закон Гука. Максимальное напряжение, при котором еще выполняется закон Гука, называется пределом пропорциональности
σп
. Он соответствует точки
А
диаграммы.
Если продолжать увеличивать нагрузку при растяжении и превзойти предел пропорциональности, то деформация становится нелинейной (линия ABCDEK
). Тем не менее при небольших нелинейных деформациях после снятия нагрузки форма и размеры тела практически восстанавливаются (участокАВ
графика).
Максимальное напряжение, при котором еще не возникают заметные остаточные деформации, называется пределом упругостиσуп
. Он соответствует точке
В
диаграммы. Предел упругости превышает предел пропорциональности не более чем на 0,33%. В большинстве случаев их можно считать равными.
Если внешняя нагрузка такова, что в теле возникают напряжения, превышающие предел упругости, то характер деформации меняется (участок BCDEK
). После снятия нагрузки образец не принимает прежние размеры, а остается деформированным, хотя и с меньшим удлинением, чем при нагрузке (пластическая деформация).
За пределом упругости при некотором значении напряжения, соответствующем точке С
диаграммы, удлинение возрастает практически без увеличения нагрузки (участокCD
диаграммы почти горизонтален). Это явление называется
текучестью материала
.
При дальнейшем увеличении нагрузки напряжение повышается (от точки D
), после чего в наименее прочной части образца появляется сужение («шейка»). Из-за уменьшения площади сечения (точкаЕ
) для дальнейшего удлинения нужно меньшее напряжение, но, в конце концов, наступает разрушение образца (точка
К
).
Наибольшее напряжение, которое выдерживает образец без разрушения, называется пределом прочности
. Обозначим его
σ
пч (оно соответствует точке
Е
диаграммы). Его значение сильно зависит от природы материала и его обработки.
Чтобы свести к минимуму возможность разрушения сооружения, инженер должен при расчетах допускать в его элементах такие напряжения, которые будут составлять лишь часть предела прочности материала. Их называют допустимыми напряжениями. Число, показывающее, во сколько раз предел прочности больше допустимого напряжения, называют коэффициентом запаса прочности
.
Обозначив запас прочности через n, получим: \(~n = \frac{\sigma_{np}}{\sigma}\) .
Запас прочности выбирается в зависимости от многих причин: качества материала, характера нагрузки (статическая или изменяющаяся со временем), степени опасности, возникающей при разрушении, и т.д. На практике запас прочности колеблется от 1,7 до 10. Выбрав правильно запас прочности, инженер может определить допустимое в конструкции напряжение.
Физический смысл модуля Юнга
Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.
Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.
Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.
В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:
Величину, обратную α, и называют модулем Юнга:
ε = (Δl) / l = α * (F/S)
Отношение растягивающей силы F к S называют упругим напряжением σ:
Закон Гука, записанный с использованием модуля Юнга, выглядит так:
Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.
В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.
Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l
Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.
Предел упругости
Согласно определению, модуль упругости показывает, какое напряжение нужно приложить к твердому телу, чтобы его деформация составила 100 %. Однако все твердые тела обладают пределом упругости, который равен 1 % деформации. Это означает, что если приложить соответствующее усилие и деформировать тело на величину, меньшую 1 %, тогда после прекращения действия этого усилия тело точно восстанавливает свою первоначальную форму и размеры. При приложении слишком большого усилия, при котором величина деформации превышает 1 %, после прекращения действия внешней силы тело уже не восстановит первоначальные размеры. В последнем случае говорят о существовании остаточной деформации, которая является свидетельством превышения упругого предела данного материала.
Значения модуля юнга для некоторых материалов
В таблице показаны значения E ряда распространенных веществ.
| Материал | модуль Юнга E, ГПа |
| Алюминий | 70 |
| Бронза | 75-125 |
| Вольфрам | 350 |
| Графен | 1000 |
| Латунь | 95 |
| Лёд | 3 |
| Медь | 110 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 200/210 |
| Стекло | 70 |
Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.
Расчетные сопротивления и модули упругости для строительных материалов
Материал
| расчетные сопротивления строительных материалов | |
| При расчете строительных конструкций нужно знать расчетное сопротивление и модуль упругости для того или иного материала. Здесь представлены данные по основным строительным материалам. Таблица 1. Модули упругости для основных строительных материалов | |
| Модуль упругости Е, МПа | |
| Чугун белый, серый | (1,15. 1,60) · 10 5 |
| Чугун ковкий | 1,55 · 10 5 |
| Сталь углеродистая | (2,0. 2,1) · 10 5 |
| Сталь легированная | (2,1. 2,2) · 10 5 |
| Медь прокатная | 1,1 · 10 5 |
| Медь холоднотянутая | 1,3 · 10 3 |
| Медь литая | 0,84 · 10 5 |
| Бронза фосфористая катанная | 1,15 · 10 5 |
| Бронза марганцевая катанная | 1,1 · 10 5 |
| Бронза алюминиевая литая | 1,05 · 10 5 |
| Латунь холоднотянутая | (0,91. 0,99) · 10 5 |
| Латунь корабельная катанная | 1,0 · 10 5 |
| Алюминий катанный | 0,69 · 10 5 |
| Проволока алюминиевая тянутая | 0,7 · 10 5 |
| Дюралюминий катанный | 0,71 · 10 5 |
| Цинк катанный | 0,84 · 10 5 |
| Свинец | 0,17 · 10 5 |
| Лед | 0,1 · 10 5 |
| Стекло | 0,56 · 10 5 |
| Гранит | 0,49 · 10 5 |
| Известь | 0,42 · 10 5 |
| Мрамор | 0,56 · 10 5 |
| Песчаник | 0,18 · 10 5 |
| Каменная кладка из гранита | (0,09. 0,1) · 10 5 |
| Каменная кладка из кирпича | (0,027. 0,030) · 10 5 |
| Бетон (см. таблицу 2) | |
| Древесина вдоль волокон | (0,1. 0,12) · 10 5 |
| Древесина поперек волокон | (0,005. 0,01) · 10 5 |
| Каучук | 0,00008 · 10 5 |
| Текстолит | (0,06. 0,1) · 10 5 |
| Гетинакс | (0,1. 0,17) · 10 5 |
| Бакелит | (2. 3) · 10 3 |
| Целлулоид | (14,3. 27,5) · 10 2 |
Нормативные данные для рассчетов железобетонных конструкций
Таблица 2. Модули упругости бетона (согласно СП 52-101-2003)
| Значения начального модуля упругости бетона при сжатии и растяжении Eb, МПа · 10 -3 , при классе бетона по прочности на сжатие | ||||||||||
| B10 | B15 | B20 | B25 | B30 | B35 | B40 | B45 | B50 | B55 | B60 |
| 19,0 | 24,0 | 27,5 | 30,0 | 32,5 | 34,5 | 36,0 | 37,0 | 38,0 | 39,0 | 39,5 |
Таблица 2.1 Модули упругости бетона согласно СНиП 2.03.01-84*(1996)
Примечания: 1. Над чертой указаны значения в МПа, под чертой — в кгс/см². 2. Для легкого, ячеистого и поризованного бетонов при промежуточных значениях плотности бетона начальные модули упругости принимают по линейной интерполяции. 3. Для ячеистого бетона неавтоклавного твердения значения Еb принимают как для бетона автоклавного твердения с умножением на коэффициент 0,8. 4. Для напрягающего бетона значения Еb принимают как для тяжелого бетона с умножением на коэффициент a
= 0,56 + 0,006В.
Таблица 3. Нормативные значения сопротивления бетона (согласно СП 52-101-2003)
Таблица 4. Расчетные значения сопротивления бетона сжатию (согласно СП 52-101-2003)
Таблица 4.1 Расчетные значения сопротивления бетона сжатию согласно СНиП 2.03.01-84*(1996)
Таблица 5. Расчетные значения сопротивления бетона растяжению (согласно СП 52-101-2003)
Таблица 6. Нормативные сопротивления для арматуры (согласно СП 52-101-2003)
Таблица 6.1 Нормативные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)
Таблица 6.2 Нормативные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)
Таблица 7. Расчетные сопротивления для арматуры (согласно СП 52-101-2003)
Таблица 7.1 Расчетные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)
Таблица 7.2 Расчетные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)
Нормативные данные для расчетов металлических контрукций
Таблица 8. Нормативные и расчетные сопротивления при растяжении, сжатии и изгибе (согласно СНиП II-23-81 (1990)) листового, широкополосного универсального и фасонного проката по ГОСТ 27772-88 для стальных конструкций зданий и сооружений
Примечания: 1. За толщину фасонного проката следует принимать толщину полки (минимальная его толщина 4 мм). 2. За нормативное сопротивление приняты нормативные значения предела текучести и временного сопротивления по ГОСТ 27772-88. 3. Значения расчетных сопротивлений получены делением нормативных сопротивлений на коэффициенты надежности по материалу, с округлением до 5 МПа (50 кгс/см²).
Таблица 9. Марки стали, заменяемые сталями по ГОСТ 27772-88 (согласно СНиП II-23-81 (1990))
Примечания: 1. Стали С345 и С375 категорий 1, 2, 3, 4 по ГОСТ 27772-88 заменяют стали категорий соответственно 6, 7 и 9, 12, 13 и 15 по ГОСТ 19281-73* и ГОСТ 19282-73*. 2. Стали С345К, С390, С390К, С440, С590, С590К по ГОСТ 27772-88 заменяют соответствующие марки стали категорий 1-15 по ГОСТ 19281-73* и ГОСТ 19282-73*, указанные в настоящей таблице. 3. Замена сталей по ГОСТ 27772-88 сталями, поставляемыми по другим государственным общесоюзным стандартам и техническим условиям, не предусмотрена.
Расчетные сопротивления для стали, используемой для производства профилированных листов здесь не показаны.
Предел прочности материала
Это предел возникающего напряжения, после которого образец начинает разрушаться.
Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.
Читать также: Температура плавления бронзы в градусах
Инструмент для определения предела прочности
Кроме того, существуют пределы прочности на сжатие материала и на растяжение. Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.
Расчет жесткости системы
Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.
Последовательное соединение системы пружин
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
1/k = 1/k1 + 1/k2 + … + 1/ki,
где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.
Параллельное соединение системы пружин
В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
k = k1 + k2 + … + ki.
Измерение жесткости пружины опытным путем — в этом видео.
https://youtube.com/watch?v=YjfWehCZnf8
Допускаемое механическое напряжение в некоторых материалах при растяжении
Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.
Испытание на растяжение
Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.
| Материалы | σраст | |
| Бор | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловолокно | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
Запасы прочности, закладываемые в ответственные конструкции, также многократны.
Механические свойства
Только при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала. А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры:
- Жёсткостью называют произведение поперечного сечения профиля на модуль упругости. По этой величине можно судить о пластичности узла конструкции в целом, а не о материале отдельно. Единицей измерения являются килограммы силы.
- Продольное относительное удлинение — это отношение абсолютного удлинения материала-образца к его общей длине. К примеру, на стержень, длина которого равна 200 миллиметров, приложили некоторую силу. В результате он стал короче на 5 миллиметров. В результате относительное удлинение будет равняться 0,05. Эта величина безразмерная. Для более удобного восприятия иногда её переводят в проценты.
- Поперечное относительное удлинение рассчитывается точно так же, как и продольное относительное удлинение, но вместо длины берут диаметр стержня. Опытным путём было установлено, что для большего количества материала поперечное меньше продольного удлинения приблизительно в 4 раза.
- Коэффициент Пуассона. Это отношения относительной продольной к относительной поперечной деформации. При помощи этой величины можно полностью описать под воздействием нагрузки изменения формы.
- Модуль сдвига описывает упругие свойства под воздействием касательных свойств на образец. Иными словами, когда вектор силы направляется к поверхности тела под 90 градусов. Примером подобных нагрузок служит работа гвоздей на смятие, заклёпок на срез и пр. Этот параметр связан с вязкостью материала.
- Модуль упругости объёмной характеризует изменение объёма образца для разностороннего равномерного приложения нагрузки. Эта величина является отношением давления объёмного к деформации сжатия объёмной. Как пример можно рассматривать опущенный в воду материал, на который воздействует давление жидкости по всей его площади.
Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства. Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.
У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.
Коэффициент запаса прочности
Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.
Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.
Области использования меди
Благодаря своим механическим свойствам медь нашла широкое применение в разных отраслях промышленности, но наиболее часто ее можно встретить как составную часть электропровода, в системах отопления, а также охлаждения воздуха, в производстве компьютерной техники, теплообменниках.
В промышленности используют тысячи тонн меди ежегодно
В строительстве этот металл применяется при изготовлении различных конструкций, основным преимуществом здесь является небольшой объемный вес меди. Как уже было отмечено выше, широкое применение цветной металл нашел при кровельных работах, а также в изготовлении тр. Трубы получаются легковесные, поддающиеся трансформации, что особенно актуально при проектировании водопровода и канализации.
Основная доля производства изделий из меди — проволока, используемая как жила для электрического или коммуникационного кабеля. Благодаря основной характеристике меди — электропроводности, она оказывает высокое сопротивление току, а также обладает уникальными магнитными качествами — в отличие от других металлов ее частицы не реагируют на магнит, что иногда затрудняет процесс ее очистки. Стоит отметить, что практически все производство изделий базируется на переработке вторичного сырья, руду используют крайне редко.
Связь с другими модулями упругости
Модуль Юнга связан с модулем сдвига, определяющим способность образца к сопротивлению против деформации сдвига, следующим соотношением:
E связан также и с модулем объёмной упругости, определяющим способность образца к сопротивлению против одновременного сжатия со всех сторон.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Одной из главных задач инженерного проектирования является выбор материала конструкции и оптимального сечения профиля. Необходимо найти тот размер, который при минимально возможной массе будет обеспечивать сохранение формы системы под воздействием нагрузки.
Например, какой номер стального двутавра использовать в качестве пролетной балки сооружения? Если взять профиль размерами ниже требуемого, то гарантировано получим разрушение строения. Если больше, то это ведет к нерациональному использованию металла, а, следовательно, утяжелению конструкции, усложнению монтажа, увеличению финансовых затрат. Знание такого понятия как модуль упругости стали даст ответ на вышепоставленный вопрос, и позволит избежать появления данных проблем на самом раннем этапе производства.
Единица измерения и формулы
Единица измерения модуля Юнга в СИ — Ньютон на метр в квадрате (Н/м²), т.е. Паскаль (Па).
Формулы
Существует несколько формул, из которых можно вычислить модуль Юнга. Например, закон Гука.
Закон Гука
Можно вычислить модуль Юнга через эти формулы (мы это и сделаем на примере). Из-за этого закона существуют несколько интересных равенств, которые могут быть полезны для расчётов.
Закон Гука (этот описывает явления в теле, в дифференциальной форме):
- σ — механическое напряжение
- E — модуль Юнга (модуль упругости)
- ε — относительное удлинение
Закон Гука (этот описывает явления в теле)
- Fупр — сила упругости
- k × Δl — удлинение тела
- Fупр — сила упругости
- E — модуль Юнга (модуль упругости)
- S — площадь поперечного сечения
- l — первоначальная длина тела
- Δl — удлинение тела
- Fупр/S — механическое напряжение, обозначается как σ
- Δl/l — относительное удлинение, обозначается как ε
Следует заметить, что этот закон действует до той точки, когда материал необратимо деформируется и уже не возвращается в свою первоначальную форму. В какой точке это происходит, уже зависит от материала. Если материал очень жёсткий (значит высокое показание модуля упругости), то эта точка может совпадать с разрывом/деформацией.
Другие формулы вычисления модуля Юнга (модуля упругости)
- E — модуль Юнга (модуль упругости)
- k — жёсткость тела
- l — первоначальная длина стержня
- S — площадь поперечного сечения
Либо можно выразить k (жёсткость тела):
- k — жёсткость тела
- E — модуль Юнга (модуль упругости)
- S — площадь поперечного сечения
- l — первоначальная длина стержня/тела
Пример решения задачи (через закон Гука):
Проволока длиной 2,5 метра и площадью поперечного сечения 2,5 миллиметра² удлинилась на 1 миллиметр под действием силы 50 ньютонов. Определить модуль Юнга.
- l = 2,5 м
- F = 50 H
- E = ?
Будем искать через закон Гука (σ = E × ε).
Помним из закона Гука:
σ = F / S (помните, что Fупр/S — механическое напряжение, обозначается как σ)
ε = Δl/l (а это относительное удлинение, обозначается как ε)
Подставляем в формулу (σ = E × ε):
Например, в нашей таблице такой модуль Юнга имеет кадмий.
Общее понятие
Модуль упругости (также известный как модуль Юнга) – один из показателей механических свойств материала, который характеризует его сопротивляемость деформации растяжения. Другими словами, его значение показывает пластичность материала. Чем больше модуль упругости, тем менее будет растягиваться какой-либо стержень при прочих равных условиях (величина нагрузки, площадь сечения и прочее).
В теории упругости модуль Юнга обозначается буквой Е. Является составной частью закона Гука (закона о деформации упругих тел). Связывает напряжение, возникающее в материале, и его деформацию.
Согласно международной стандартной системе единиц измеряется в МПа. Но на практике инженеры предпочитают использовать размерность кгс/см2.
Определение модуля упругости осуществляется опытным путем в научных лабораториях. Суть данного способа заключается в разрыве на специальном оборудовании гантелеобразных образцов материала. Узнав напряжение и удлинение, при котором произошло разрушение образца, делят данные переменные друг на друга, тем самым получая модуль Юнга.
Отметим сразу, что таким методом определяются модули упругости пластичных материалов: сталь, медь и прочее. Хрупкие материалы – чугун, бетон – сжимают до появления трещин.
Дополнительные характеристики механических свойств
Модуль упругости дает возможность предугадать поведение материла только при работе на сжатие или растяжение. При наличии таких видов нагрузок как смятие, срез, изгиб и прочее потребуется введение дополнительных параметров:
- Жесткость есть произведение модуля упругости на площадь поперечного сечения профиля. По величине жесткости можно судить о пластичности уже не материала, а узла конструкции в целом. Измеряется в килограммах силы.
- Относительное продольное удлинение показывает отношение абсолютного удлинения образца к общей длине образца. Например, к стержню длиной 100 мм приложили определенную силу. Как результат, он уменьшился в размере на 5 мм. Деля его удлинение (5 мм) на первоначальную длину (100 мм) получаем относительное удлинение 0,05. Переменная является безразмерной величиной. В некоторых случаях для удобства восприятия переводится в проценты.
- Относительное поперечное удлинение рассчитывается аналогично вышепредставленному пункту, но вместо длины здесь рассматривается диаметр стержня. Опыты показывают, что для большинства материалов поперечное удлинение в 3-4 раза меньше, чем продольное.
- Коэффициент Пуансона есть отношение относительной продольной деформации к относительной поперечной деформации. Данный параметр позволяет полностью описать изменение формы под воздействием нагрузки.
- Модуль сдвига характеризует упругие свойства при воздействии на образец касательных напряжений, т. е. в случае, когда вектор силы направлен под 90 градусов к поверхности тела. Примерами таких нагрузок является работа заклепок на срез, гвоздей на смятие и прочее. По большому счету, модуль сдвига связан с таким понятием как вязкость материла.
- Модуль объемной упругости характеризуется изменением объема материала для равномерного разностороннего приложения нагрузки. Является отношением объемного давления к объемной деформации сжатия. Примером такой работы служит опущенный в воду образец, на который по всей его площади воздействует давление жидкости.
Читать также: Что происходит с металлом при охлаждении
Помимо вышесказанного необходимо упомянуть, что некоторые типы материалов имеют различные механические свойства в зависимости от направления нагрузки. Такие материалы характеризуются как анизотропные. Яркими примерами служит древесина, слоистые пластмассы, некоторые виды камня, ткани и прочее.
У изотропных материалов механические свойства и упругая деформация одинаковы в любом направлении. К ним относят металлы (сталь, чугун, медь, алюминий и прочее), неслоистые пластмассы, естественные камни, бетон, каучук.
Что представляет собой медь
Cuprum
Одним из наиболее распространенных цветных металлов, используемых в промышленности, является медь, ее название на латинском Cuprum, в честь острова Кипра, где ее добывали греки много тысяч лет назад. Это один из семи металлов, которые были известны еще в глубокой древности, из него делали украшения, посуду, деньги, орудия.
Историками даже назван период (с IV по III тысячелетие до нашей эры) Медным Веком. Д. И. Менделеев поставил этот металл на 29-е место в своей таблице, после водорода, поскольку медь не вытесняет его из кислотной среды. Медь — цветной металл, который имеет уникальные физические, механический, химические свойства.
Плотность меди в кг м³ является одной из важнейших характеристик, с ее помощью определяется вес будущего изделия.
Как определяется плотность
Плотность любого вещества — показатель отношения массы к общему объему. Наиболее распространенной системой измерения величины плотности является килограмм на кубический метр. Для меди этот показатель равен 8,93 кг/м³. Поскольку существуют различные марки металла, которые различаются в зависимости от примесей других веществ, общий показатель плотности может изменяться. В данном случае уместней использовать другую характеристику — удельный вес. В измерительных системах этот показатель выражается в разных величинах:
Формула определения плотности вещества
- система СГС — дин/см³;
- система СИ — н/м³;
- система МКСС — кг/м³
При этом для перевода величин можно использовать следующую формулу:
1 н/м³ = 1 дин/см³ = 0,102 кг/м³.
Удельный вес — важный показатель при производстве различных материалов, содержащих медь, особенно когда речь идет о ее сплавах. Это величина отношения массы меди в общем объеме сплава.
Рассмотреть как применяется этот показатель на практике, можно на примере расчета веса 25 медных листов, размером 2000*1000 мм, толщиной 5 мм. Для начала определим объем листа — 5 мм * 2000 мм * 1000 мм = 10000000 мм3 или 10 000 см³.
Удельный вес меди 8, 94 гр/см³
Рассчитываем вес меди в одном листе — 10 000 * 8,94 = 89 400 гр или 89, 40 кг.
Масса медного проката в общем количестве материала — 89, 40 * 25 = 2 235 кг.
Эта схема расчета применяется и при переработке лома металла.
Основные свойства
Выплавка меди из руды
Медь, как металл, получается при выплавке руды, в природе сложно найти чистые самородки в основном обогащение и добыча осуществляется из:
- халькозиновой руды, в которой содержание меди около 80%, этот вид часто называют медным блеском;
- бронитовой руды, здесь содержание металла до 65%
- ковеллиновой руды — до 64%.
По своим физическим свойствам медь представляет собой красного цвета металл, в разрезе может присутствовать розовый отлив, относится к тяжелым металлам, поскольку имеет высокую плотность.
Отличительной характеристикой является электропроводность. Благодаря этому металл широко применяется при изготовлении кабелей и электропроводов. По этому показателю медь уступает только серебру, кроме того, имеется ряд других физических характеристик:
- твердость — по шкале Бринделя равняется 35 кгс/мм²;
- упругость — 132000 Мн/м²;
- линейное термическое расширение — 0,00000017 единицы;
- относительное удлинение — 60%;
- температура плавления — 1083 ºС;
- температура кипения — 2600 ºС;
- коэффициент теплопроводности — 335 ккал/м*ч*град.
Значение модуля упругости
Необходимо заметить, что модуль Юнга не является постоянной величиной. Даже для одного и того же материала он может колебаться в зависимости от точек приложения силы.
Некоторые упруго – пластичные материалы обладают более или менее постоянным модулем упругости при работе как на сжатие, так и на растяжение: медь, алюминий, сталь. В других случаях упругость может изменяться исходя из формы профиля.
Вот примеры значений модуля Юнга (в миллионах кгссм2) некоторых материалов:
- Чугун белый – 1,15.
- Чугун серый -1,16.
- Латунь – 1,01.
- Бронза – 1,00.
- Кирпичная каменная кладка – 0,03.
- Гранитная каменная кладка – 0,09.
- Бетон – 0,02.
- Древесина вдоль волокон – 0,1.
- Древесина поперек волокон – 0,005.
- Алюминий – 0,7.
Рассмотрим разницу в показаниях между модулями упругости для сталей в зависимости от марки:
- Стали конструкционные высокого качества (20, 45) – 2,01.
- Стали обычного качества (Ст.3, Ст.6) – 2,00.
- Стали низколегированные (30ХГСА, 40Х) – 2,05.
- Стали нержавеющие (12Х18Н10Т) – 2,1.
- Стали штамповые (9ХМФ) – 2,03.
- Стали пружинные (60С2) – 2,03.
- Стали подшипниковые (ШХ15) – 2,1.
Также значение модуля упругости для сталей изменяется исходя из вида проката:
- Проволока высокой прочности – 2,1.
- Плетенный канат – 1,9.
- Трос с металлическим сердечником – 1,95.
Как видим, отклонения между сталями в значениях модулей упругой деформации имеют небольшую величину. Поэтому в большинстве инженерных расчетов можно пренебречь погрешностями и брать значение Е=2,0.
Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.
Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними. Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда. С повышением прочностных характеристик совершенствовались инструменты и способы производства.
Модуль упругости Юнга и сдвига, коэффициент Пуассона значения (Таблица)
Упругие свойства тел
Ниже приводятся справочные таблицы общеупотребительных констант; если известны две их них, то этого вполне достаточно для определения упругих свойств однородного изотропного твердого тела.
Модуль Юнга или модуль продольной упругости в дин/см2.
Модуль сдвига или модуль кручения G в дин/см2.
Модуль всестороннего сжатия или модуль объемной упругости К в дин/см2.
Объем сжимаемости k=1/K/.
Коэффициент Пуассона µ равен отношению поперечного относительного сжатия к продольному относительному растяжению.
Для однородного изотропного твердого материала имеют место следующие соотношения между этими константами:
G = E / 2(1 + μ) — (α)
μ = (E / 2G) — 1 — (b)
K = E / 3(1 — 2μ) — (c)
Коэффициент Пуассона имеет положительный знак, и его значение обычно заключено в пределах от 0,25 до 0,5, но в некоторых случаях он может выходить за указанные пределы. Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.
Таблицы значений Модуля упругости Юнга, Модуля сдвига и коэффициента Пуассона
Курсивом даны значения, вычисленные из соотношений (a), (b), (c).
| Материал при 18°С | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
| Алюминий | 7,05 | 2,62 | 0,345 | 7,58 |
| Висмут | 3,19 | 1,20 | 0,330 | 3,13 |
| Железо | 21,2 | 8,2 | 0,29 | 16,9 |
| Золото | 7,8 | 2,7 | 0,44 | 21,7 |
| Кадмий | 4,99 | 1,92 | 0,300 | 4,16 |
| Медь | 12,98 | 4,833 | 0,343 | 13,76 |
| Никель | 20,4 | 7,9 | 0,280 | 16,1 |
| Платина | 16,8 | 6,1 | 0,377 | 22,8 |
| Свинец | 1,62 | 0,562 | 0,441 | 4,6 |
| Серебро | 8,27 | 3,03 | 0,367 | 10,4 |
| Титан | 11,6 | 4,38 | 0,32 | 10,7 |
| Цинк | 9,0 | 3,6 | 0,25 | 6,0 |
| Сталь (1% С) 1) | 21,0 | 8,10 | 0,293 | 16,88 |
| (мягкая) | 21,0 | 8,12 | 0,291 | 16,78 |
| Константан 2) | 16,3 | 6,11 | 0,327 | 15,7 |
| Манганин | 12,4 | 4,65 | 0,334 | 12,4 |
| 1) Для стали, содержащий около 1% С, упругие константы, как известно , меняются при термообработке. 2) 60% Cu, 40% Ni. |
Экспериментальные результаты, приводимые ниже, относятся к обычным лабораторным материалам, главным образом проволокам.
| Вещество | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
| Бронза (66% Cu) | -9,7-10,2 | 3,3-3,7 | 0,34-0,40 | 11,2 |
| Медь | 10,5-13,0 | 3,5-4,9 | 0,34 | 13,8 |
| Нейзильбер1) | 11,6 | 4,3-4,7 | 0,37 | — |
| Стекло | 5,1-7,1 | 3,1 | 0,17-0,32 | 3,75 |
| Стекло иенское крон | 6,5-7,8 | 2,6-3,2 | 0,20-0,27 | 4,0-5,9 |
| Стекло иенское флинт | 5,0-6,0 | 2,0-2,5 | 0,22-0,26 | 3,6-3,8 |
| Железо сварочное | 19-20 | 7,7-8,3 | 0,29 | 16,9 |
| Чугун | 10-13 | 3,5-5,3 | 0,23-0,31 | 9,6 |
| Магний | 4,25 | 1,63 | 0,30 | — |
| Бронза фосфористая2) | 12,0 | 4,36 | 0,38 | — |
| Платиноид3) | 13,6 | 3,6 | 0,37 | — |
| Кварцевые нити (плав.) | 7,3 | 3,1 | 0,17 | 3,7 |
| Резина мягкая вулканизированная | 0,00015-0,0005 | 0,00005-0,00015 | 0,46-0,49 | — |
| Сталь | 20-21 | 7,9-8,9 | 0,25-0,33 | 16,8 |
| Цинк | 8,7 | 3,8 | 0,21 | — |
| 1) 60% Cu, 15% Ni, 25% Zn 2) 92,5% Cu, 7% Sn, 0,5% P 3) Нейзильбер с небольшим количеством вольфрама. |
| Вещество | Модуль Юнга E, 1011 дин/см2. | Вещество | Модуль Юнга E, 1011 дин/см2. |
| Цинк (чистый) | 9,0 | Дуб | 1,3 |
| Иридий | 52,0 | Сосна | 0,9 |
| Родий | 29,0 | Красное дерево | 0,88 |
| Тантал | 18,6 | Цирконий | 7,4 |
| Инвар | 17,6 | Титан | 10,5-11,0 |
| Сплав 90% Pt, 10% Ir | 21,0 | Кальций | 2,0-2,5 |
| Дюралюминий | 7,1 | Свинец | 0,7-1,6 |
| Шелковые нити1 | 0,65 | Тиковое дерево | 1,66 |
| Паутина2 | 0,3 | Серебро | 7,1-8,3 |
| Кетгут | 0,32 | Пластмассы: | |
| Лед (-20С) | 0,28 | Термопластичные | 0,14-0,28 |
| Кварц | 7,3 | Термореактивные | 0,35-1,1 |
| Мрамор | 3,0-4,0 | Вольфрам | 41,1 |
| 1) Быстро уменьшается с увеличением нагрузки 2) Обнаруживает заметную упругую усталость |
| Температурный коэффициент (при 150С) Et=E11 (1-ɑ (t-15)), Gt=G11 (1-ɑ (t-15)) | Сжимаемость k, бар-1 (при 7-110С) | |||
| ɑ, для Е | ɑ, для G | |||
| Алюминий | 4,8*10-4 | 5,2*10-4 | Алюминий | 1,36*10-6 |
| Латунь | 3,7*10-4 | 4,6*10-4 | Медь | 0,73*10-6 |
| Золото | 4,8*10-4 | 3,3*10-4 | Золото | 0,61*10-6 |
| Железо | 2,3*10-4 | 2,8*10-4 | Свинец | 2,1*10-6 |
| Сталь | 2,4*10-4 | 2,6*10-4 | Магний | 2,8*10-6 |
| Платина | 0,98*10-4 | 1,0*10-4 | Платина | 0,36*10-6 |
| Серебро | 7,5*10-4 | 4,5*10-4 | Стекло флинт | 3,0*10-6 |
| Олово | — | 5,9*10-4 | Стекло немецкое | 2,57*10-6 |
| Медь | 3,0*10-4 | 3,1*10-4 | Сталь | 0,59*10-6 |
| Нейзильбер | — | 6,5*10-4 | ||
| Фосфористая бронза | — | 3,0*10-4 | ||
| Кварцевые нити | -1,5*10-4 | -1,1*10-4 |
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
- Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.
Читать также: Как сделать гравировку на дереве
- Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.
- Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
- Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
- Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.
Основные свойства
Выплавка меди из руды
Медь, как металл, получается при выплавке руды, в природе сложно найти чистые самородки в основном обогащение и добыча осуществляется из:
- халькозиновой руды, в которой содержание меди около 80%, этот вид часто называют медным блеском;
- бронитовой руды, здесь содержание металла до 65%
- ковеллиновой руды — до 64%.
По своим физическим свойствам медь представляет собой красного цвета металл, в разрезе может присутствовать розовый отлив, относится к тяжелым металлам, поскольку имеет высокую плотность.
Отличительной характеристикой является электропроводность. Благодаря этому металл широко применяется при изготовлении кабелей и электропроводов. По этому показателю медь уступает только серебру, кроме того, имеется ряд других физических характеристик:
- твердость — по шкале Бринделя равняется 35 кгс/мм²;
- упругость — 132000 Мн/м²;
- линейное термическое расширение — 0,00000017 единицы;
- относительное удлинение — 60%;
- температура плавления — 1083 ºС;
- температура кипения — 2600 ºС;
- коэффициент теплопроводности — 335 ккал/м*ч*град.
К основным свойствам меди относят показатель модулей упругости, которые рассчитываются различными методами:
Модуль сдвига полезно знать при производстве материалов для строительной отрасли — это величина, которая характеризует степень сопротивление сдвигу и деформации под воздействием различных нагрузок. Модуль, рассчитанный по методике Юнга, показывает как будет вести себя металл при одноосном растяжении. Модуль сдвига характеризует отклик металла на сдвиговую нагрузку. Коэффициент Пуассона показывает как ведет себя материал при всестороннем сжатии.
Разработка рудников по добычи меди и других металлов
Химические свойства меди описывают соединение с другими веществами в сплавы, возможные реакции на кислотную среду. Наиболее значимой характеристикой является окисление. Этот процесс активно проявляется во время нагревания, уже при температуре 375 ºС начинает формироваться оксид меди, или как его называют окалина, которая может влиять на проводниковые функции металла, снижать их.
При взаимодействии меди с раствором соли железа она переходит в жидкое состояние. Этот метод используют для того чтобы снять медное напыление на различных изделиях.
Долгое пребывание в воде вызывает куприт
При длительном воздействии на медь влажной среды на ее поверхности образуется куприт — зеленоватый налет. Это свойство меди учитывают при использовании метала для покрытия крыш. Примечательно, что куприт выполняет защитную функцию, металл под ним совершенно не портится, даже на протяжении ста лет. Единственными противниками крыш из медного материала являются экологи. Свою позицию они объясняют тем, что при смыве куприта меди дождевыми водами в почву или водоемы, он загрязняет ее своими токсинами, особенно это пагубно влияет на микроорганизмы, живущие в реках и озерах. Но для решения этой проблемы строители используют водосточные трубы из специального металла, который поглощает медные частицы в себя и накапливает, при этом вода стекает очищенной от токсинов.
Медный купорос — еще один результат химического воздействия на металл. Это вещество активно используют агрономы для удобрения почвы и стимулирования роста различных сельскохозяйственных культур. Однако бесконтрольное использование купороса может также пагубно влиять на экологию. Токсины проникают глубоко в слои земли и накапливаются в подземных водах.
Понятие о модуле упругости
В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
- Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
- Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).
Формула по закону Гука записывается в виде ε = σz/E, где:
- ε – относительное удлинение;
- σz – нормальное напряжение.
Демонстрация закона Гука для упругих тел:
Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.
В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.
Значения модуля упругости для некоторых материалов приведены в таблице 1.
Таблица 1: Модуль упругости для металлов и сплавов
| Наименование материала | Значение модуля упругости, 10¹²·Па |
| Алюминий | 65…72 |
| Дюралюминий | 69…76 |
| Железо, содержание углерода менее 0,08 % | 165…186 |
| Латунь | 88…99 |
| Медь (Cu, 99 %) | 107…110 |
| Никель | 200…210 |
| Олово | 32…38 |
| Свинец | 14…19 |
| Серебро | 78…84 |
| Серый чугун | 110…130 |
| Сталь | 190…210 |
| Стекло | 65…72 |
| Титан | 112…120 |
| Хром | 300…310 |
Что это такое?
Модуль упругости (модуль Юнга) – показатель, определяющий механическую реакцию материала. При помощи данного параметра удается охарактеризовать поведение образца при растяжении. Если говорить более простым языком, то модуль упругости означает пластичные свойства стали, и чем выше показатель, тем меньше растяжение. В теории модуль Юнга обозначают буквой «Е». Это один из компонентов закона Гука, в котором рассматриваются возможные деформации упругих тел. Посредством данной величины удается связать возникающие в материале напряжения с деформацией, которую он испытывает. Единица измерения модуля упругости – паскали (Па) или мегапаскали (МПа). Однако часто инженеры при проведении расчетов отдают предпочтение кгс/см2. Показатель определяют путем исследований в лабораториях, фиксируя образцы на специальном оборудовании. В основе методики лежит разрыв образцов в форме гантелей на автоматизированных установках.
В ходе эксперимента автоматика отслеживает показатели изменения длины и натяжения заготовки, при которых она разрушается, а затем делит результаты. Полученное число и будет модулем Юнга или модулем упругости. Примечательно, что подобная методика определения показателя используется для определения Е:
- стали;
- меди;
- других упругих образцов.
В хрупких материалах параметр определяют путем сжатия до момента появления трещин. Стоит подробнее остановиться на разборе модуля Юнга с точки зрения физики. В процессе принудительного нагружения, которое приводит к изменению формы материала, внутри него возникают ответные усилия. Силы начинают оказывать сопротивление напряжениям извне и стремятся вернуть форму тела. Если образец совершенно не реагирует на нагрузку (точнее, полностью меняет форму и не восстанавливает ее при снятии усилий), его принято считать пластичным. В качестве примера стоит назвать пластилин, который наглядно отражает теорию на практике. Исследованием упругости материалов занимался ученый Р. Гук, которого интересовало, как будут меняться и удлиняться стержни разных материалов под воздействием гирь. Благодаря ранее проведенной серии опытов удалось доказать, что величины абсолютного удлинения и исходной длины прямо пропорциональны. В то же время абсолютное удлинение обратно пропорционально площади поперечного сечения исследуемого стержня.
Гук вывел целый закон, а также ввел параметр Е для характеристики свойств упругого материала. Таким образом, физический смысл модуля заключается в том, что параметр соответствует напряжению, вызываемому в стержне при растягивании на длину, которая в два раза выше при условии отсутствия видимых разрушений образца.
Посредством модуля Е удается предугадать, как будет вести себя материал при определенных нагружениях. Однако он не дает понимания того, что с ним произойдет при других способах нагружения. Поэтому для проведения эффективных расчетов необходимо введение дополнительных параметров.
- Жесткость. Показатель демонстрирует степень пластичности узла исследуемого образца. Единица измерения параметра – кгс.
- Относительное удлинение в продольном направлении. При расчете используются два показателя: величина абсолютного удлинения и общая длина образца. Показатель не имеет единицы измерения, однако для упрощенного понимания его умножают на 100%.
- Относительное удлинение в поперечном направлении. Высчитывается таким же образом, как и предыдущий параметр, только вместо длины используют диаметр стержня-образца. Как показали испытания, поперечное удлинение обычно меньше продольного.
- Коэффициент Пуассона. Представляет собой соотношение двух последних показателей. Параметр делает возможным описание того, как материал будет менять свою форму, опираясь на величину нагрузки и место ее приложения.
- Модуль сдвига. С его помощью удается описать поведение материала с упругими свойствами при воздействии сил по касательной. Другими словами, помогает оценить работу конструкции при воздействии на нее ветра под углом в 90 градусов.
Модуль упругости для разных марок стали
Металлурги разработали несколько сотен марок сталей. Им свойственны разные значения прочности. В таблице 2 показаны характеристики для наиболее распространенных сталей.
Таблица 2: Упругость сталей
| Наименование стали | Значение модуля упругости, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 |
| Сталь 3 | 179…189 |
| Сталь 30 | 194…205 |
| Сталь 45 | 211…223 |
| Сталь 40Х | 240…260 |
| 65Г | 235…275 |
| Х12МФ | 310…320 |
| 9ХС, ХВГ | 275…302 |
| 4Х5МФС | 305…315 |
| 3Х3М3Ф | 285…310 |
| Р6М5 | 305…320 |
| Р9 | 320…330 |
| Р18 | 325…340 |
| Р12МФ5 | 297…310 |
| У7, У8 | 302…315 |
| У9, У10 | 320…330 |
| У11 | 325…340 |
| У12, У13 | 310…315 |
Видео: закон Гука, модуль упругости.
Модули прочности
Кроме нормального нагружения, существуют и иные силовые воздействия на материалы.
Модуль сдвига G определяет жесткость. Эта характеристика показывает предельное значение нагрузки изменению формы предмета.
Модуль объемной упругости К определяет упругие свойства материала изменить объем. При любой деформации происходит изменение формы предмета.
Для разных сталей значения указанных модулей приведены в таблице 3.
Таблица 3: Модули прочности для сталей
| Наименование стали | Модуль упругости Юнга, 10¹²·Па | Модуль сдвига G, 10¹²·Па | Модуль объемной упругости, 10¹²·Па | Коэффициент Пуассона, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 | 87…91 | 45…49 | 154…168 |
| Сталь 3 | 179…189 | 93…102 | 49…52 | 164…172 |
| Сталь 30 | 194…205 | 105…108 | 72…77 | 182…184 |
| Сталь 45 | 211…223 | 115…130 | 76…81 | 192…197 |
| Сталь 40Х | 240…260 | 118…125 | 84…87 | 210…218 |
| 65Г | 235…275 | 112…124 | 81…85 | 208…214 |
| Х12МФ | 310…320 | 143…150 | 94…98 | 285…290 |
| 9ХС, ХВГ | 275…302 | 135…145 | 87…92 | 264…270 |
| 4Х5МФС | 305…315 | 147…160 | 96…100 | 291…295 |
| 3Х3М3Ф | 285…310 | 135…150 | 92…97 | 268…273 |
| Р6М5 | 305…320 | 147…151 | 98…102 | 294…300 |
| Р9 | 320…330 | 155…162 | 104…110 | 301…312 |
| Р18 | 325…340 | 140…149 | 105…108 | 308…318 |
| Р12МФ5 | 297…310 | 147…152 | 98…102 | 276…280 |
| У7, У8 | 302…315 | 154…160 | 100…106 | 286…294 |
| У9, У10 | 320…330 | 160…165 | 104…112 | 305…311 |
| У11 | 325…340 | 162…170 | 98…104 | 306…314 |
| У12, У13 | 310…315 | 155…160 | 99…106 | 298…304 |
Для других материалов значения прочностных характеристик указывают в специальной литературе. Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.
Модуль деформации стали и её упругости
Основной главной задачей инженерного проектирования служит выбор оптимального сечения профиля и материала конструкции. Нужно найти именно тот размер, который обеспечит сохранение формы системы при минимальной возможной массе под влиянием нагрузки. К примеру, какую именно сталь следует применять в качестве пролётной балки сооружения? Материал может использоваться нерационально, усложнится монтаж и утяжелится конструкция, увеличатся финансовые затраты. На этот вопрос ответит такое понятие как модуль упругости стали. Он же позволит на самой ранней стадии избежать появления этих проблем.