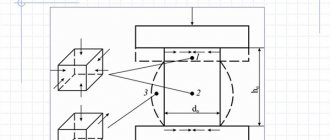
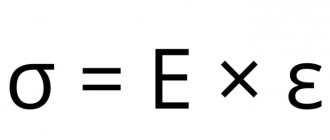Показатель несжимаемости / устойчивости к сжимаемости вещества.
Иллюстрация равномерного сжатия
Объемный модуль упругости
( или ) вещества является мерой того , насколько устойчивым к сжатию , что вещество. Он определяется как отношение бесконечно малого увеличения давления к результирующему
относительному
уменьшению объема . [1] Другие модули описывают реакцию материала ( деформацию ) на другие виды напряжения : модуль сдвига описывает реакцию на сдвиг, а модуль Юнга описывает реакцию на линейное напряжение. Для жидкости значение имеет только модуль объемной упругости. Для сложного анизотропного твердого тела, такого как K {\ displaystyle K} B {\ displaystyle B} дерево или бумага , эти три модуля не содержат достаточно информации, чтобы описать его поведение, и необходимо использовать полный обобщенный закон Гука .
Определение [ править ]
Объемный модуль упругости можно формально определить уравнением K > 0 {\ displaystyle K> 0}
K знак равно — V d п d V {\ displaystyle K = -V {\ frac {dP} {dV}}}
где — давление, — начальный объем вещества, а обозначает производную давления по объему. Учитывая единицу массы, п {\ displaystyle P} V {\ displaystyle V} d п / d V {\ displaystyle dP / dV}
K знак равно ρ d п d ρ {\ Displaystyle К = \ ро {\ гидроразрыва {дП} {д \ ро}}}
где ρ
— начальная плотность, а d
P
/ d
ρ
обозначает производную давления по плотности (т.е. скорость изменения давления в зависимости от объема). Обратный модуль объемного сжатия дает сжимаемость вещества .
Термодинамическое соотношение [ править ]
Строго говоря, объемный модуль упругости является термодинамической величиной, и для того, чтобы указать объемный модуль, необходимо указать, как давление изменяется во время сжатия: постоянная температура (изотермическая ), постоянная энтропия ( изэнтропическая ) и другие варианты возможны. . Такие различия особенно актуальны для газов . K Т {\ displaystyle K_ {T}} K S {\ displaystyle K_ {S}}
Для идеального газа изэнтропический процесс имеет:
п V γ знак равно c о п s т . ⇒ п ∝ ( 1 V ) γ ∝ ρ γ , {\ Displaystyle PV ^ {\ gamma} = const. \, \ Rightarrow P \ propto \ left ({\ frac {1} {V}} \ right) ^ {\ gamma} \ propto \ rho ^ {\ gamma}, }
поэтому изоэнтропический модуль объемной упругости определяется как: K S {\ displaystyle K_ {S}}
K S знак равно γ п . {\ displaystyle K_ {S} = \ gamma P.}
Точно так же изотермический процесс идеального газа имеет:
п V знак равно c о п s т . ⇒ п ∝ 1 V ∝ ρ , {\displaystyle PV=const.\,\Rightarrow P\propto {\frac {1}{V}}\propto \rho ,}
поэтому изотермический модуль объемной упругости определяется выражением K T {\displaystyle K_{T}}
K T = P {\displaystyle K_{T}=P}
где γ
представляет собой отношение теплоемкости и
р
является давлением.
Когда газ не идеален, эти уравнения дают только приближение модуля объемного сжатия. В жидкости объемный модуль K
и плотность
ρ
определяют скорость звука
c
( волны давления ) в соответствии с формулой Ньютона-Лапласа
c = K ρ . {\displaystyle c={\sqrt {\frac {K}{\rho }}}.}
В твердых телах и имеют очень похожие значения. Твердые тела также могут выдерживать поперечные волны : для этих материалов требуется один дополнительный модуль упругости , например модуль сдвига, для определения скорости волны. K S {\displaystyle K_{S}} K T {\displaystyle K_{T}}
Общие понятия
Модуль упругости (модуль Юнга) — это показатель механического свойства материала, характеризующий его сопротивляемость деформации растяжения. Иными словами, это значение пластичности материала. Чем выше значения модуля упругости, тем меньше будет какой-либо стержень растягиваться при иных равных нагрузках (площадь сечения, величина нагрузки и другие).
Модуль Юнга в теории упругости обозначается буквой Е. Он является составляющей закона Гука (о деформации упругих тел). Эта величина связывает возникающее в образце напряжение и его деформацию.
Измеряется эта величина согласно стандартной международной системе единиц в МПа (Мегапаскалях). Но инженеры на практике больше склоняются к применению размерности кгс/см2.
Опытным путём осуществляется определение этого показателя в научных лабораториях. Сутью этого метода является разрыв гантелеобразных образцов материала на специальном оборудовании. Узнав удлинение и натяжение, при которых образец разрушился, делят переменные данные друг на друга. Полученная величина и является модулем (Юнга) упругости.
Таким образом определяется только модуль Юнга материалов упругих: медь, сталь и прочее. А материалы хрупкие сжимают до того момента, пока не появятся трещины: бетон, чугун и им подобные.
Выбранные значения [ править ]
Приблизительный модуль объемной упругости (K) для обычных материалов
| Материал | Объемный модуль в ГПа | Магистральный модуль в МПСИ |
| Резина [2] | 1,5 к2 | От 0,22 до0,29 |
| Натрия хлорид | 24,42 | 3,542 |
| Стекло (см. Также схему под таблицей) | От 35 до55 | 5,8 |
| Стали | 160 | 23,2 |
| Diamond (в разрешении 4K) [3] | 443 | 64 |
| Гранит | 50 | 7.3 |
| Сланец | 10 | 1.5 |
| Известняк | 65 | 9,4 |
| Мел | 9 | 1.3 |
| Песчаник | 0,7 | 0,1 |
Влияние добавок выбранных стеклянных компонентов на модуль объемной упругости определенного базового стекла. [4]
Материал с объемным модулем упругости 35 ГПа теряет один процент своего объема при воздействии внешнего давления 0,35 ГПа (~3500 бар ).
Приблизительный модуль объемной упругости (K) для других веществ
| Вода | 2,2 ГПа (значение увеличивается при повышении давления) |
| Метанол | 823 МПа (при 20 ° C и 1 Атм) |
| Воздуха | 142 кПа (адиабатический объемный модуль [или изоэнтропический объемный модуль]) |
| Воздуха | 101 кПа (изотермический модуль объемной упругости) |
| Твердый гелий | 50 МПа (приблизительно) |
Физические свойства жидкостей
Глава 1. ОСНОВЫ ГИДРОСТАТИКИ
Основными физическими свойствами жидкости являются: текучесть, плотность, удельный вес, вязкость, сжимаемость, температурное расширение.
Плотность жидкости – физическая величина, численно равная отношению массы жидкости к ее объёму.
(1.1)
где r
– плотность жидкости,
кг
/
м
3;
m
– масса жидкости;
кг
;
W
– объём жидкости,
м
3.
Удельный вес – физическая величина, численно равная отношению веса жидкости к ее объёму.
(1.2)
где g
– удельный вес жидкости,
Н
/
м
3;
G
– вес жидкости,
Н
.
Между удельным весом g
и плотностью
r
имеется зависимость
(1.3
где g
= 9,81
м
/
с
2 – ускорение свободного падения.
Значения r
и
g
для воды и некоторых других жидкостей при различной температуре приведены в приложении 1.
Вязкость – свойство жидкости оказывать сопротивление относительному сдвигу смежных слоёв. Вязкость характеризуется коэффициентами динамической вязкости m
,
Па×с
, и
кинематической вязкости n
,
м
/
с
. Между этими коэффициентами имеется зависимость
(1.4)
Значения коэффициентов динамической и кинематической вязкости для некоторых жидкостей приведены в приложении 2.
Сжимаемость – свойство жидкости изменять свой объём при изменении давления. Сжимаемость характеризуется коэффициентом объёмного сжатия b
w, который можно определить по формуле
(1.5)
где b
w – коэффициент объёмного сжатия, 1/
Па
;
W
– первоначальный объём жидкости,
м
3;
DW
– изменение объёма жидкости,
м
3;
Dp
– изменение давления,
Па
.
Величина, обратная коэффициенту объёмного сжатия, называется модулем объёмной упругости К
. Модуль объёмной упругости измеряется в
Па
.
(1.6)
Коэффициенты объёмного сжатия жидкостей мало меняются при изменении температуры и давления. Значение коэффициентов объёмного сжатия и модулей упругости для некоторых жидкостей приведены в приложении 3.
Температурное расширение – свойство жидкости изменять свой объём при изменении температуры. Температурное расширение характеризуется коэффициентом температурного расширения , который может быть определен из выражения
(1.7)
где – коэффициент температурного расширения, 1/К
;
W
– первоначальный объём жидкости,
м
3;
– изменение объёма жидкости, м
3;
– изменение температуры, К
.
Коэффициенты температурного расширения для некоторых жидкостей приведены в приложении 4.
Задачи
1.1. Определить массу воды в рукаве диаметром 51 мм
и длиной 20
м.
Решение. Масса воды определяется из формулы (1.1)
Плотность воды по приложению 1
Объём воды
Тогда
1.2. Определить вес воды в рукавах диаметром 66 мм
и 77
мм
и дли-ной 20
м
.
1.3. Определить массу дизельного мазута, находящегося в цистерне объёмом 50 м
3, если плотность мазута составляет 920
кг
/
м
3.
1.4. Определить, какой объём займет нефть, имеющая массу 20×103кг
и плотность 900
кг
/
м
3.
1.5. Определить плотность нефтепродуктов, если их масса составляет 17,5×103кг
, объём 20
м
3.
1.6. Определить вес этилового спирта в объёме 20 литров.
1.7. Уровень мазута в вертикальном цилиндрическом баке диаметром 2 м
понизился на 0,5
м
. Определить массу израсходованного мазута, если его плотность при температуре 20 °
С
равна 990
кг
/
м
3.
1.8. При гидравлических испытаниях допускается утечка воды, которая за одни сутки не должна превышать 3 л
с квадратного метра смоченной поверхности. Возможно ли принять в эксплуатацию резервуар прямоугольной формы, имеющий размеры в плане 12´6
м
, в котором уровень воды за одни сутки понизился с 3,5
м
до 3,48
м
. Определить массу убывшей воды.
Решение. Объём убывшей воды составил
Масса убывшей воды
Площадь смоченной поверхности
Утечка воды с одного квадратного метра смоченной поверхности при гидравлических испытаниях
что превышает установленную норму.
1.9. Определить, возможно ли принять в эксплуатацию цилиндрический резервуар диаметром 12 м
, в котором уровень воды за одни сутки понизился с 5
м
до 4,985
м
.
1.10. Определить предельную массу воды, убывшей за одни сутки в результате гидравлических испытаний цилиндрического резервуара диаметром 18 м
. Определить предельное снижение уровня воды, если первоначальный уровень составлял 3,9
м
.
1.11. Определить коэффициент динамической вязкости нефти, если коэффициент кинематической вязкости составляет 0,624×10-4м
2/
с
. Плотность нефти 750
кг
/
м
3.
1.12. Водовод пожарного водопровода диаметром 300 мм
и длиной 50
м
, подготовленный к гидравлическим испытаниям, заполнен водой при атмосферном давлении. Определить объём воды, которую необходимо дополнительно подать в водовод, чтобы избыточное давление в нем поднялось до 5
МПа
. Деформацией труб водовода пренебречь.
Решение. Из уравнения (1.5) находим, что объём воды, который необходимо дополнительно подать в водовод, определяется как
Коэффициент объёмного сжатия воды
Первоначальный объём воды
Тогда
1.13. При гидравлическом испытании технологического трубопровода длиной 200 м
и диаметром 250
мм
, заполненного керосином, давление было поднято до 1,5
МПа
. Через один час давление упало до 1,0
МПа
. Определить объём вытекшего через неплотность керосина. Коэффициент объёмного сжатия керосина принять = 80×10-11 1/
Па
. Деформацией трубопровода пре- небречь.
1.14. Манометр на технологической емкости, полностью заполненной нефтью, показывает 0,5 МПа
. При выпуске 40
л
нефти показания манометра упали до 0,1
МПа
. Определить объём ёмкости, если коэффициент объёмного сжатия нефти = 80×10-11 1/Па.
1.15. В вертикальном цилиндрическом резервуаре диаметром 5 м
находится 1,2×105
кг
нефти, плотность которой при 0 °
С
составляет 800
кг
/
м
3. Определить колебания уровня нефти в резервуаре при изменении температуры от 0 °
С
до 30 °
С
.
1.16. Определить колебания уровня воды в баке водонапорной башни при изменении температуры от 10 °С
до 35 °
С
. В водонапорном баке диаметром 3
м
находится 20
м
3 воды. Коэффициент температурного расширения воды принять равным 2×10-4 1/
К
.
1.17. Предельная высота уровня бензола в вертикальном цилиндрическом резервуаре диаметром 12 м
равна 10
м
при температуре 10 °
С
. Определить, до какого уровня возможно налить бензол при возможном повышении температуры до 30 °
С
. Расширением резервуара пренебречь.
Глава 1. ОСНОВЫ ГИДРОСТАТИКИ
Основными физическими свойствами жидкости являются: текучесть, плотность, удельный вес, вязкость, сжимаемость, температурное расширение.
Плотность жидкости – физическая величина, численно равная отношению массы жидкости к ее объёму.
(1.1)
где r
– плотность жидкости,
кг
/
м
3;
m
– масса жидкости;
кг
;
W
– объём жидкости,
м
3.
Удельный вес – физическая величина, численно равная отношению веса жидкости к ее объёму.
(1.2)
где g
– удельный вес жидкости,
Н
/
м
3;
G
– вес жидкости,
Н
.
Между удельным весом g
и плотностью
r
имеется зависимость
(1.3
где g
= 9,81
м
/
с
2 – ускорение свободного падения.
Значения r
и
g
для воды и некоторых других жидкостей при различной температуре приведены в приложении 1.
Вязкость – свойство жидкости оказывать сопротивление относительному сдвигу смежных слоёв. Вязкость характеризуется коэффициентами динамической вязкости m
,
Па×с
, и
кинематической вязкости n
,
м
/
с
. Между этими коэффициентами имеется зависимость
(1.4)
Значения коэффициентов динамической и кинематической вязкости для некоторых жидкостей приведены в приложении 2.
Сжимаемость – свойство жидкости изменять свой объём при изменении давления. Сжимаемость характеризуется коэффициентом объёмного сжатия b
w, который можно определить по формуле
(1.5)
где b
w – коэффициент объёмного сжатия, 1/
Па
;
W
– первоначальный объём жидкости,
м
3;
DW
– изменение объёма жидкости,
м
3;
Dp
– изменение давления,
Па
.
Величина, обратная коэффициенту объёмного сжатия, называется модулем объёмной упругости К
. Модуль объёмной упругости измеряется в
Па
.
(1.6)
Коэффициенты объёмного сжатия жидкостей мало меняются при изменении температуры и давления. Значение коэффициентов объёмного сжатия и модулей упругости для некоторых жидкостей приведены в приложении 3.
Температурное расширение – свойство жидкости изменять свой объём при изменении температуры. Температурное расширение характеризуется коэффициентом температурного расширения , который может быть определен из выражения
(1.7)
где – коэффициент температурного расширения, 1/К
;
W
– первоначальный объём жидкости,
м
3;
– изменение объёма жидкости, м
3;
– изменение температуры, К
.
Коэффициенты температурного расширения для некоторых жидкостей приведены в приложении 4.
Задачи
1.1. Определить массу воды в рукаве диаметром 51 мм
и длиной 20
м.
Решение. Масса воды определяется из формулы (1.1)
Плотность воды по приложению 1
Объём воды
Тогда
1.2. Определить вес воды в рукавах диаметром 66 мм
и 77
мм
и дли-ной 20
м
.
1.3. Определить массу дизельного мазута, находящегося в цистерне объёмом 50 м
3, если плотность мазута составляет 920
кг
/
м
3.
1.4. Определить, какой объём займет нефть, имеющая массу 20×103кг
и плотность 900
кг
/
м
3.
1.5. Определить плотность нефтепродуктов, если их масса составляет 17,5×103кг
, объём 20
м
3.
1.6. Определить вес этилового спирта в объёме 20 литров.
1.7. Уровень мазута в вертикальном цилиндрическом баке диаметром 2 м
понизился на 0,5
м
. Определить массу израсходованного мазута, если его плотность при температуре 20 °
С
равна 990
кг
/
м
3.
1.8. При гидравлических испытаниях допускается утечка воды, которая за одни сутки не должна превышать 3 л
с квадратного метра смоченной поверхности. Возможно ли принять в эксплуатацию резервуар прямоугольной формы, имеющий размеры в плане 12´6
м
, в котором уровень воды за одни сутки понизился с 3,5
м
до 3,48
м
. Определить массу убывшей воды.
Решение. Объём убывшей воды составил
Масса убывшей воды
Площадь смоченной поверхности
Утечка воды с одного квадратного метра смоченной поверхности при гидравлических испытаниях
что превышает установленную норму.
1.9. Определить, возможно ли принять в эксплуатацию цилиндрический резервуар диаметром 12 м
, в котором уровень воды за одни сутки понизился с 5
м
до 4,985
м
.
1.10. Определить предельную массу воды, убывшей за одни сутки в результате гидравлических испытаний цилиндрического резервуара диаметром 18 м
. Определить предельное снижение уровня воды, если первоначальный уровень составлял 3,9
м
.
1.11. Определить коэффициент динамической вязкости нефти, если коэффициент кинематической вязкости составляет 0,624×10-4м
2/
с
. Плотность нефти 750
кг
/
м
3.
1.12. Водовод пожарного водопровода диаметром 300 мм
и длиной 50
м
, подготовленный к гидравлическим испытаниям, заполнен водой при атмосферном давлении. Определить объём воды, которую необходимо дополнительно подать в водовод, чтобы избыточное давление в нем поднялось до 5
МПа
. Деформацией труб водовода пренебречь.
Решение. Из уравнения (1.5) находим, что объём воды, который необходимо дополнительно подать в водовод, определяется как
Коэффициент объёмного сжатия воды
Первоначальный объём воды
Тогда
1.13. При гидравлическом испытании технологического трубопровода длиной 200 м
и диаметром 250
мм
, заполненного керосином, давление было поднято до 1,5
МПа
. Через один час давление упало до 1,0
МПа
. Определить объём вытекшего через неплотность керосина. Коэффициент объёмного сжатия керосина принять = 80×10-11 1/
Па
. Деформацией трубопровода пре- небречь.
1.14. Манометр на технологической емкости, полностью заполненной нефтью, показывает 0,5 МПа
. При выпуске 40
л
нефти показания манометра упали до 0,1
МПа
. Определить объём ёмкости, если коэффициент объёмного сжатия нефти = 80×10-11 1/Па.
1.15. В вертикальном цилиндрическом резервуаре диаметром 5 м
находится 1,2×105
кг
нефти, плотность которой при 0 °
С
составляет 800
кг
/
м
3. Определить колебания уровня нефти в резервуаре при изменении температуры от 0 °
С
до 30 °
С
.
1.16. Определить колебания уровня воды в баке водонапорной башни при изменении температуры от 10 °С
до 35 °
С
. В водонапорном баке диаметром 3
м
находится 20
м
3 воды. Коэффициент температурного расширения воды принять равным 2×10-4 1/
К
.
1.17. Предельная высота уровня бензола в вертикальном цилиндрическом резервуаре диаметром 12 м
равна 10
м
при температуре 10 °
С
. Определить, до какого уровня возможно налить бензол при возможном повышении температуры до 30 °
С
. Расширением резервуара пренебречь.
Микроскопическое происхождение [ править ]
Межатомный потенциал и линейная эластичность [ править ]
Межатомный потенциал и сила
Поскольку линейная эластичность является прямым результатом межатомного взаимодействия, она связана с растяжением / сжатием связей. Затем его можно вывести из межатомного потенциала кристаллических материалов. [5] Во-первых, давайте рассмотрим потенциальную энергию двух взаимодействующих атомов. Начиная с очень далеких точек, они почувствуют влечение друг к другу. По мере приближения друг к другу их потенциальная энергия будет уменьшаться. С другой стороны, когда два атома находятся очень близко друг к другу, их полная энергия будет очень высокой из-за отталкивающего взаимодействия. Вместе эти потенциалы гарантируют межатомное расстояние, при котором достигается минимальное энергетическое состояние. Это происходит на некотором расстоянии a 0 , где полная сила равна нулю:
F = − ∂ U ∂ r = 0 {\displaystyle F=-{\partial U \over \partial r}=0}
Где U — межатомный потенциал, а r — межатомное расстояние. Это означает, что атомы находятся в равновесии.
Для того, чтобы расширить два атома подойти в твердое тело, рассмотрит модель простой, скажем, 1-D массив одного элемента с межатомным расстоянием A A, и равновесное расстояние 0 . Его потенциальная энергия-межатомное расстояние связь имеет аналогичную форму , как и случае два атома, который достигает минимально в виде
0 , разложение в ряд Тейлора для этого является:
u ( a ) = u ( a 0 ) + ( ∂ u ∂ r ) r = a 0 ( a − a 0 ) + 1 2 ( ∂ 2 ∂ r 2 u ) r = a 0 ( a − a 0 ) 2 + O ( ( a − a 0 ) 3 ) {\displaystyle u(a)=u(a_{0})+\left({\partial u \over \partial r}\right)_{r=a_{0}}(a-a_{0})+{1 \over 2}\left({\partial ^{2} \over \partial r^{2}}u\right)_{r=a_{0}}(a-a_{0})^{2}+O\left((a-a_{0})^{3}\right)}
В состоянии равновесия первая производная равна 0, поэтому доминирующий член — квадратичный. Когда смещение невелико, члены более высокого порядка следует опускать. Выражение становится:
u ( a ) = u ( a 0 ) + 1 2 ( ∂ 2 ∂ r 2 u ) r = a 0 ( a − a 0 ) 2 {\displaystyle u(a)=u(a_{0})+{1 \over 2}\left({\partial ^{2} \over \partial r^{2}}u\right)_{r=a_{0}}(a-a_{0})^{2}} F ( a ) = − ∂ u ∂ r = ( ∂ 2 ∂ r 2 u ) r = a 0 ( a − a 0 ) {\displaystyle F(a)=-{\partial u \over \partial r}=\left({\partial ^{2} \over \partial r^{2}}u\right)_{r=a_{0}}(a-a_{0})}
Это явно линейная эластичность.
Обратите внимание, что вывод выполняется с учетом двух соседних атомов, поэтому коэффициент Хука равен:
K = a 0 ∗ d F d r = a 0 ( ∂ 2 ∂ r 2 u ) r = a 0 {\displaystyle K=a_{0}*{dF \over dr}=a_{0}\left({\partial ^{2} \over \partial r^{2}}u\right)_{r=a_{0}}}
Эта форма может быть легко расширена до трехмерного случая с объемом на атом (Ω) вместо межатомного расстояния.
K = Ω 0 ( ∂ 2 ∂ Ω 2 u ) Ω = Ω 0 {\displaystyle K=\Omega _{0}\left({\partial ^{2} \over \partial \Omega ^{2}}u\right)_{\Omega =\Omega _{0}}}
Связь с атомным радиусом [ править ]
Как было установлено выше, объемный модуль напрямую связан с межатомным потенциалом и объемом, приходящимся на атом. Мы можем дополнительно оценить межатомный потенциал, чтобы связать K
с другими свойствами. Обычно межатомный потенциал может быть выражен как функция расстояния, которая имеет два члена: один член для притяжения, а другой — для отталкивания.
u = − A r − n + B r − m {\displaystyle u=-Ar^{-n}+Br^{-m}}
Где A
> 0 представляет член притяжения, а
B
> 0 представляет отталкивание. n и m обычно являются целыми, а
m
обычно больше
n
, что отражает характер отталкивания на короткие расстояния. В положении равновесия
u
минимально, поэтому производная первого порядка равна 0.
( ∂ u ∂ r ) r 0 = A n r − n − 1 + − B m r − m − 1 = 0 {\displaystyle \left({\partial u \over \partial r}\right)_{r_{0}}=Anr^{-n-1}+-Bmr^{-m-1}=0} B A = n m r 0 m − n {\displaystyle {B \over A}={n \over m}r_{0}^{m-n}} u = − A r − n ( 1 − B A r n − m ) = − A r − n ( 1 − n m r 0 m − n r n − m ) {\displaystyle u=-Ar^{-n}\left(1-{B \over A}r^{n-m}\right)=-Ar^{-n}\left(1-{n \over m}r_{0}^{m-n}r^{n-m}\right)}
когда r
близко к, вспомните, что
n
(обычно от 1 до 6) меньше
m
(обычно от 9 до 12), игнорируйте второй член, оцените вторую производную
( ∂ 2 ∂ r 2 u ) r = a 0 = − A n ( n + 1 ) r 0 − n − 2 {\displaystyle \left({\partial ^{2} \over \partial r^{2}}u\right)_{r=a_{0}}=-An(n+1)r_{0}^{-n-2}}
Напомним связь между r и Ω
Ω = 4 π 3 r 3 {\displaystyle \Omega ={4\pi \over 3}r^{3}} ( ∂ 2 ∂ Ω 2 u ) = ( ∂ 2 ∂ r 2 u ) ( ∂ r ∂ Ω ) 2 = ( ∂ 2 ∂ r 2 u ) Ω − 4 3 {\displaystyle \left({\partial ^{2} \over \partial \Omega ^{2}}u\right)=\left({\partial ^{2} \over \partial r^{2}}u\right)\left({\partial r \over \partial \Omega }\right)^{2}=\left({\partial ^{2} \over \partial r^{2}}u\right)\Omega ^{-{\frac {4}{3}}}} K = Ω 0 ( ∂ 2 u ∂ r 2 ) Ω = Ω 0 ∝ r 0 − n − 3 {\displaystyle K=\Omega _{0}\left({\partial ^{2}u \over \partial r^{2}}\right)_{\Omega =\Omega _{0}}\propto r_{0}^{-n-3}}
Во многих случаях, например, в металлических или ионных материалах, сила притяжения является электростатической, поэтому n
= 1, мы имеем
K ∝ r 0 − 4 {\displaystyle K\propto r_{0}^{-4}}
Это относится к атомам со схожей природой связи. Эта взаимосвязь подтверждается для щелочных металлов и многих ионных соединений. [6]
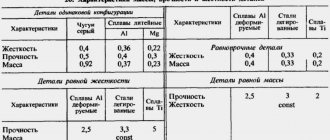
Модуль упругости различных материалов
Модули упругости для различных материалов имеют совершенно разные значения, которые зависят от:
- природы веществ, формирующих состав материала;
- моно- или многокомпонентный состав (чистое вещество, сплав и так далее);
- структуры (металлическая или другой вид кристаллической решетки, молекулярное строение прочее);
- плотности материала (распределения частиц в его объеме);
- обработки, которой он подвергался (обжиг, травление, прессование и тому подобное).
Так, например, в справочных данных можно найти, что модуль упругости для алюминия составляет диапазон от 61,8 до 73,6 ГПа. Видимо, это и зависит от состояния металла и вида обработки, потому как для отожженного алюминия модуль Юнга – 68,5 ГПа.
Его значение для бронзовых материалов зависит не только от обработки, но и от химического состава:
- бронза – 10,4 ГПа;
- алюминиевая бронза при литье – 10,3 ГПа;
- фосфористая бронза катанная – 11,3 ГПа.
Модуль Юнга латуни на много ниже – 78,5-98,1. Максимальное значение имеет катанная латунь.
Сама же медь в чистом виде характеризуется сопротивлением к внешним воздействиям значительно большим, чем ее сплавы – 128,7 ГПа. Обработка ее также снижает показатель, в том числе и прокатка:
- литая – 82 ГПа;
- прокатанная – 108 ГПа;
- деформированная – 112 ГПа;
- холоднотянутая – 127 ГПа.
Близким значением к меди обладает титан (108 ГПа), который считается одним из самых прочных металлов. А вот тяжелый, но ломкий свинец, показывает всего 15,7-16,2 ГПа, что сравнимо с прочностью древесины.
Для железа показатель напряжения к деформации также зависит от метода его обработки: литое – 100-130 или кованное – 196,2-215,8 ГПа.
Чугун известен своей хрупкостью имеет отношение напряжения к деформации от 73,6 до 150 ГПа, что соответствует от его виду. Тогда как для стали модуль упругости может достигать 235 ГПа.
Модули упругости некоторых материалов
На величины параметров прочности влияют также и формы изделий. Например, для стального каната проводят расчеты, где учитывают:
- его диаметр;
- шаг свивки;
- угол свивки.
Интересно, что этот показатель для каната будет значительно ниже, чем для проволоки такого же диаметра.
Стоит отметить прочность и не металлических материалов. Например, среди модулей Юнга дерева наименьший у сосны – 8,8 ГПа, а вот у группы твердых пород, которые объединены под названием «железное дерево» самый высокий – 32,5 ГПа, дуб и бук имеют равные показатели – 16,3 ГПа.
Среди строительных материалов, сопротивление к внешним силам у, казалось бы, прочного гранита всего 35-50 ГПа, когда даже у стекла – 78 ГПа. Уступают стеклу бетон – до 40 ГПа, известняк и мрамор, со значениями 35 и 50 ГПа соответственно.
Такие гибкие материалы, как каучук и резина, выдерживают осевую нагрузку от 0,0015 до 0,0079 ГПа.
Ссылки [ править ]
- «Объемные упругие свойства» . гиперфизика
. Государственный университет Джорджии. - «Силиконовая резина» . Материалы AZO
. - Страница 52 из « Введение в физику твердого тела , 8-е издание» Чарльза Киттеля, 2005, ISBN 0-471-41526-X
- Флюгель, Александр. «Расчет объемного модуля стекол» . glassproperties.com
. - Х., Кортни, Томас (2013). Механическое поведение материалов
(2-е изд. Reimp ed.). Нью-Дели: McGraw Hill Education (Индия). ISBN 978-1259027512. OCLC 929663641 . - Перейти
↑ Gilman, JJ (1969).
Микромеханика течения в твердых телах
. Нью-Йорк: Макгроу-Хилл. п. 29.
Дальнейшее чтение [ править ]
- Де Йонг, Мартен; Чен, Вэй (2015). «Диаграмма полных упругих свойств неорганических кристаллических соединений» . Научные данные
.
2
: 150009. Bibcode : 2013NatSD … 2E0009D . DOI : 10.1038 / sdata.2015.9 . PMC 4432655 . PMID 25984348 .
| vтеМодули упругости для однородных изотропных материалов | |
| |
| Формулы преобразования | |||||||
| Однородные изотропные линейные упругие материалы обладают своими упругими свойствами, однозначно определяемыми любыми двумя модулями среди них; таким образом, для любых двух любых других модулей упругости можно рассчитать по этим формулам. | |||||||
| K = {\displaystyle K=\,} | E = {\displaystyle E=\,} | λ = {\displaystyle \lambda =\,} | G = {\displaystyle G=\,} | ν = {\displaystyle \nu =\,} | M = {\displaystyle M=\,} | Примечания | |
| ( K , E ) {\displaystyle (K,\,E)} | 3 K ( 3 K − E ) 9 K − E {\displaystyle {\tfrac {3K(3K-E)}{9K-E}}} | 3 K E 9 K − E {\displaystyle {\tfrac {3KE}{9K-E}}} | 3 K − E 6 K {\displaystyle {\tfrac {3K-E}{6K}}} | 3 K ( 3 K + E ) 9 K − E {\displaystyle {\tfrac {3K(3K+E)}{9K-E}}} | |||
| ( K , λ ) {\displaystyle (K,\,\lambda )} | 9 K ( K − λ ) 3 K − λ {\displaystyle {\tfrac {9K(K-\lambda )}{3K-\lambda }}} | 3 ( K − λ ) 2 {\displaystyle {\tfrac {3(K-\lambda )}{2}}} | λ 3 K − λ {\displaystyle {\tfrac {\lambda }{3K-\lambda }}} | 3 K − 2 λ {\displaystyle 3K-2\lambda \,} | |||
| ( K , G ) {\displaystyle (K,\,G)} | 9 K G 3 K + G {\displaystyle {\tfrac {9KG}{3K+G}}} | K − 2 G 3 {\displaystyle K-{\tfrac {2G}{3}}} | 3 K − 2 G 2 ( 3 K + G ) {\displaystyle {\tfrac {3K-2G}{2(3K+G)}}} | K + 4 G 3 {\displaystyle K+{\tfrac {4G}{3}}} | |||
| ( K , ν ) {\displaystyle (K,\,\nu )} | 3 K ( 1 − 2 ν ) {\displaystyle 3K(1-2\nu )\,} | 3 K ν 1 + ν {\displaystyle {\tfrac {3K\nu }{1+\nu }}} | 3 K ( 1 − 2 ν ) 2 ( 1 + ν ) {\displaystyle {\tfrac {3K(1-2\nu )}{2(1+\nu )}}} | 3 K ( 1 − ν ) 1 + ν {\displaystyle {\tfrac {3K(1-\nu )}{1+\nu }}} | |||
| ( K , M ) {\displaystyle (K,\,M)} | 9 K ( M − K ) 3 K + M {\displaystyle {\tfrac {9K(M-K)}{3K+M}}} | 3 K − M 2 {\displaystyle {\tfrac {3K-M}{2}}} | 3 ( M − K ) 4 {\displaystyle {\tfrac {3(M-K)}{4}}} | 3 K − M 3 K + M {\displaystyle {\tfrac {3K-M}{3K+M}}} | |||
| ( E , λ ) {\displaystyle (E,\,\lambda )} | E + 3 λ + R 6 {\displaystyle {\tfrac {E+3\lambda +R}{6}}} | E − 3 λ + R 4 {\displaystyle {\tfrac {E-3\lambda +R}{4}}} | 2 λ E + λ + R {\displaystyle {\tfrac {2\lambda }{E+\lambda +R}}} | E − λ + R 2 {\displaystyle {\tfrac {E-\lambda +R}{2}}} | R = E 2 + 9 λ 2 + 2 E λ {\displaystyle R={\sqrt {E^{2}+9\lambda ^{2}+2E\lambda }}} | ||
| ( E , G ) {\displaystyle (E,\,G)} | E G 3 ( 3 G − E ) {\displaystyle {\tfrac {EG}{3(3G-E)}}} | G ( E − 2 G ) 3 G − E {\displaystyle {\tfrac {G(E-2G)}{3G-E}}} | E 2 G − 1 {\displaystyle {\tfrac {E}{2G}}-1} | G ( 4 G − E ) 3 G − E {\displaystyle {\tfrac {G(4G-E)}{3G-E}}} | |||
| ( E , ν ) {\displaystyle (E,\,\nu )} | E 3 ( 1 − 2 ν ) {\displaystyle {\tfrac {E}{3(1-2\nu )}}} | E ν ( 1 + ν ) ( 1 − 2 ν ) {\displaystyle {\tfrac {E\nu }{(1+\nu )(1-2\nu )}}} | E 2 ( 1 + ν ) {\displaystyle {\tfrac {E}{2(1+\nu )}}} | E ( 1 − ν ) ( 1 + ν ) ( 1 − 2 ν ) {\displaystyle {\tfrac {E(1-\nu )}{(1+\nu )(1-2\nu )}}} | |||
| ( E , M ) {\displaystyle (E,\,M)} | 3 M − E + S 6 {\displaystyle {\tfrac {3M-E+S}{6}}} | M − E + S 4 {\displaystyle {\tfrac {M-E+S}{4}}} | 3 M + E − S 8 {\displaystyle {\tfrac {3M+E-S}{8}}} | E − M + S 4 M {\displaystyle {\tfrac {E-M+S}{4M}}} | S = ± E 2 + 9 M 2 − 10 E M {\displaystyle S=\pm {\sqrt {E^{2}+9M^{2}-10EM}}} Есть два верных решения. Знак плюс ведет к . ν ≥ 0 {\displaystyle \nu \geq 0} Знак минус ведет к . ν ≤ 0 {\displaystyle \nu \leq 0} | ||
| ( λ , G ) {\displaystyle (\lambda ,\,G)} | λ + 2 G 3 {\displaystyle \lambda +{\tfrac {2G}{3}}} | G ( 3 λ + 2 G ) λ + G {\displaystyle {\tfrac {G(3\lambda +2G)}{\lambda +G}}} | λ 2 ( λ + G ) {\displaystyle {\tfrac {\lambda }{2(\lambda +G)}}} | λ + 2 G {\displaystyle \lambda +2G\,} | |||
| ( λ , ν ) {\displaystyle (\lambda ,\,\nu )} | λ ( 1 + ν ) 3 ν {\displaystyle {\tfrac {\lambda (1+\nu )}{3\nu }}} | λ ( 1 + ν ) ( 1 − 2 ν ) ν {\displaystyle {\tfrac {\lambda (1+\nu )(1-2\nu )}{\nu }}} | λ ( 1 − 2 ν ) 2 ν {\displaystyle {\tfrac {\lambda (1-2\nu )}{2\nu }}} | λ ( 1 − ν ) ν {\displaystyle {\tfrac {\lambda (1-\nu )}{\nu }}} | Не может использоваться, когда ν = 0 ⇔ λ = 0 {\displaystyle \nu =0\Leftrightarrow \lambda =0} | ||
| ( λ , M ) {\displaystyle (\lambda ,\,M)} | M + 2 λ 3 {\displaystyle {\tfrac {M+2\lambda }{3}}} | ( M − λ ) ( M + 2 λ ) M + λ {\displaystyle {\tfrac {(M-\lambda )(M+2\lambda )}{M+\lambda }}} | M − λ 2 {\displaystyle {\tfrac {M-\lambda }{2}}} | λ M + λ {\displaystyle {\tfrac {\lambda }{M+\lambda }}} | |||
| ( G , ν ) {\displaystyle (G,\,\nu )} | 2 G ( 1 + ν ) 3 ( 1 − 2 ν ) {\displaystyle {\tfrac {2G(1+\nu )}{3(1-2\nu )}}} | 2 G ( 1 + ν ) {\displaystyle 2G(1+\nu )\,} | 2 G ν 1 − 2 ν {\displaystyle {\tfrac {2G\nu }{1-2\nu }}} | 2 G ( 1 − ν ) 1 − 2 ν {\displaystyle {\tfrac {2G(1-\nu )}{1-2\nu }}} | |||
| ( G , M ) {\displaystyle (G,\,M)} | M − 4 G 3 {\displaystyle M-{\tfrac {4G}{3}}} | G ( 3 M − 4 G ) M − G {\displaystyle {\tfrac {G(3M-4G)}{M-G}}} | M − 2 G {\displaystyle M-2G\,} | M − 2 G 2 M − 2 G {\displaystyle {\tfrac {M-2G}{2M-2G}}} | |||
| ( ν , M ) {\displaystyle (\nu ,\,M)} | M ( 1 + ν ) 3 ( 1 − ν ) {\displaystyle {\tfrac {M(1+\nu )}{3(1-\nu )}}} | M ( 1 + ν ) ( 1 − 2 ν ) 1 − ν {\displaystyle {\tfrac {M(1+\nu )(1-2\nu )}{1-\nu }}} | M ν 1 − ν {\displaystyle {\tfrac {M\nu }{1-\nu }}} | M ( 1 − 2 ν ) 2 ( 1 − ν ) {\displaystyle {\tfrac {M(1-2\nu )}{2(1-\nu )}}} | |||