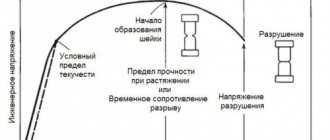
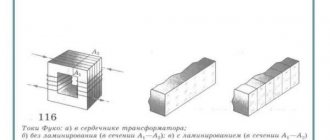
Почему возникает сопротивление
Электроны, сталкиваясь с заряженными атомами (ионами), из которых стоит кристаллическая решетка проводника, теряют скорость. Масса атома значительно превосходит массу электрона, поэтому их столкновение приводит к потере скорости (“торможению”) и изменению направления движения электрона. Таким образом возникает сопротивление протеканию (нарастанию) тока. Значит сопротивление — это физическая величина.
Столкновения электронов с атомами.
В чем измеряется
Согласно международной системе единиц, измеряется величина в омах, умноженных на метр. В некоторых случаях применяется единица ом, умноженная на миллиметр в квадрате, поделенная на метр. Это обозначение для проводника, имеющего метровую длину и миллиметровую площадь сечения в квадрате.
Единица измерения
Формула как найти
Согласно положению из любого учебного пособия по электродинамики, удельное сопротивление материала проводника формула равна пропорции общего сопротивления проводника на площадь поперечного сечения, поделенного на проводниковую длину. Важно понимать, что на конечный показатель будет влиять температура и степень материальной чистоты. К примеру, если в медь добавить немного марганца, то общий показатель будет увеличен в несколько раз.
Главная формула расчета
Интересно, что существует формула для неоднородного изотропного материала. Для этого нужно знать напряженность электрополя с плотностью электротока. Для нахождения нужно поделить первую величину на другую. В данном случае получится не константа, а скалярная величина.
Закон ома в дифференциальной форме
Есть другая, более сложная для понимания формула для неоднородного анизотропного материала. Зависит от тензорного координата.
Важно отметить, что связь сопротивления с проводимостью также выражается формулами. Существуют правила для нахождения изотропных и анизотропных материалов через тензорные компоненты. Они показаны ниже в схеме.
Связь с проводимостью, выраженная в физических соотношениях
Опыты по установлению величин, от которых зависит сопротивление
Причина электрического сопротивления кроется во взаимодействии электронов с ионами кристаллической решетки металла. Логично предположить, что сопротивление будет зависеть от рода вещества, из которого он состоит. Также мы предположим, что есть некоторая зависимость от длины проводника и площади его поперечного сечения.
Теперь давайте проведем опыты, которые подтвердят или опровергнут наши предположения.
Соберем электрическую цепь из источника тока, ключа, амперметра и реостата. Реостат — это прибор, который позволит нам изменять силу тока в цепи. Подробнее о нем вы узнаете в отдельном уроке.
В эту цепь мы будем поочередно подключать различные проводники. К ним же параллельно подсоединим вольтметр (рисунок 1).
Рисунок 1. Определение зависимости сопротивления проводника от его размеров и рода вещества
Какие проводники мы будем подключать в цепь?
Вариантов может быть огромное множество. Мы рассмотрим следующие:
- Никелиновые проволоки одинаковой толщины (с одинаковой площадью поперечных сечений), но разной длины
- Такие же никелиновые проволоки, но теперь одинаковой длины и разной толщины (с различной площадью поперечных сечений)
- Никелиновую и нихромовую проволоки одинаковой длины и толщины
Каждый раз мы будем фиксировать значения силы тока в цепи, показанные амперметром. Вольтметр даст нам значения напряжения на концах каждого проводника.
Далее, используя закон Ома для участка цепи, мы сможем рассчитать сопротивление каждого проводника по формуле $I = \frac{U}{R}$.
От чего зависит
Сопротивляемость зависит от температуры. Она увеличивается, когда повышается столбик термометра. Это поясняется физиками так, что при росте температуры атомные колебания в кристаллической проводниковой решетке повышаются. Это препятствует тому, чтобы свободные электроны двигались.
Обратите внимание! Что касается полупроводников и диэлектриков, то там величина понижается из-за того, что увеличивается структура концентрации зарядных носителей.
Зависимость от температуры как основное свойство проводниковой сопротивляемости
Что означают показатели удельного сопротивления?
Для того чтобы иметь возможность сравнивать удельное сопротивление различных материалов, от таких изделий, как медь и алюминий, до других металлов и веществ, включая висмут, латунь и даже полупроводники, необходимо использовать стандартное измерение.
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м.
Единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м2, изготовленный из этого вещества, имеет сопротивление, равное 1 Ом. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м2
Удельное сопротивление разных материалов
Важно отметить, что сопротивление у металлических монокристаллов с металлами и сплавами разные. Значения различаются из-за химической металлической чистоты, способов создания составов и их непостоянства. Также стоит иметь в виду, что значения меняются при изменении температуры. Иногда сопротивляемость падает до нуля. В таком случае явление называется сверхпроводимостью.
Интересно, что под термической обработкой, например, отжигом меди, значение вырастает в 3 раза, несмотря на то, что доля примесей в проном, антикоррозийном и легком составе, как правило, равна не больше 0,1%.
Обратите внимание! Что касается отжига алюминия, свинца или железа, значение в таких же условиях вырастает в 2 раза, несмотря на наличие примесей в количестве 0,5% и необходимости большей энергии на плавление.
Таблица значений составов при температуре 20 градусов Цельсия
В целом, удельное электросопротивление представляет собой физическую величину, которая характеризует способность вещества препятствовать тому, чтобы проходил электроток. По СИ измеряется в омах, перемноженных на метры. Зависит от увеличения температуры вещества. Отыскать значение можно по формуле соотношения общего сопротивления и площади поперечного сечения, поделенного на длину проводника. Что касается удельного сопротивления сплавов, согласно изучениям разных ученых состав их непостоянный, может быть изменен под термообработкой.
Таблица удельного сопротивления для распространенных проводников
В таблице ниже приведены показатели удельного сопротивления для различных материалов, в частности металлов, используемых для электропроводности.
Показатели удельного сопротивления приведены для таких «популярных» материалов, как медь, алюминий, нихром, сталь, свинец, золото и других.
МатериалУдельное сопротивление, ρ,при 20 °C (Ом·м)Источник
| Латунь | ~0.6 — 0.9 x 10-7 | |
| Серебро | 1.59×10−8 | [3][4] |
| Медь | 1.68×10−8 | [5][6] |
| Обожжённая медь | 1.72×10−8 | [7] |
| Золото | 2.44×10−8 | [3] |
| Алюминий | 2.65×10−8 | [3] |
| Кальций | 3.36×10−8 | |
| Вольфрам | 5.60×10−8 | [3] |
| Цинк | 5.90×10−8 | |
| Кобальт | 6.24×10−8 | |
| Никель | 6.99×10−8 | |
| Рутений | 7.10×10−8 | |
| Литий | 9.28×10−8 | |
| Железо | 9.70×10−8 | [3] |
| Платина | 1.06×10−7 | [3] |
| Олово | 1.09×10−7 | |
| Тантал | 1.3×10−7 | |
| Галлий | 1.40×10−7 | |
| Ниобий | 1.40×10−7 | [8] |
| Углеродистая сталь (1010) | 1.43×10−7 | [9] |
| Свинец | 2.20×10−7 | [2][3] |
| Галинстан | 2.89×10−7 | [10] |
| Титан | 4.20×10−7 | |
| Электротехническая сталь | 4.60×10−7 | [11] |
| Манганин (сплав) | 4.82×10−7 | [2] |
| Константан (сплав) | 4.90×10−7 | [2] |
| Нержавеющая сталь | 6.90×10−7 | |
| Ртуть | 9.80×10−7 | [2] |
| Марганец | 1.44×10−6 | |
| Нихром (сплав) | 1.10×10−6 | [2][3] |
| Углерод (аморфный) | 5×10−4 — 8×10−4 | [3] |
| Углерод (графит) параллельно-базальная плоскость | 2.5×10−6 — 5.0×10−6 | |
| Углерод (графит) перпендикулярно-базальная плоскость | 3×10−3 | |
| Арсенид галлия | 10−3 to 108 | |
| Германий | 4.6×10−1 | [3][4] |
| Морская вода | 2.1×10−1 | |
| Вода в плавательном бассейне | 3.3×10−1 — 4.0×10−1 | |
| Питьевая вода | 2×101 — 2×103 | |
| Кремний | 2.3×103 | [2][3] |
| Древесина (влажная) | 103 — 104 | |
| Деионизированная вода | 1.8×105 | |
| Стекло | 1011 — 1015 | [3][4] |
| Углерод (алмаз) | 1012 | |
| Твердая резина | 1013 | [3] |
| Воздух | 109 — 1015 | |
| Древесина (сухая) | 1014 — 1016 | |
| Сера | 1015 | [3] |
| Плавленый кварц | 7.5×1017 | [3] |
| ПЭТ | 1021 | |
| Тефлон | 1023 — 1025 |
Видно, что удельное сопротивление меди и удельное сопротивление латуни оба низкие, и с учетом их стоимости, относительно серебра и золота, они становятся экономически эффективными материалами для использования для многих проводов. Удельное сопротивление меди и простота ее использования привели к тому, что она также используется крайне часто в качестве материала для проводников на печатных платах.
Изредка алюминий и особенно медь используются из-за их низкого удельного сопротивления. Большинство проводов, используемых в наши дни для межсоединений, изготовлены из меди, поскольку она обеспечивает низкий уровень удельного сопротивления при приемлемой стоимости.
Удельное сопротивление золота также важно, поскольку золото используется в некоторых критических областях, несмотря на его стоимость. Часто золотое покрытие встречается на высококачественных слаботочных разъемах, где оно обеспечивает самое низкое сопротивление контактов. Золотое покрытие очень тонкое, но даже в этом случае оно способно обеспечить требуемые характеристики разъемов.
Серебро имеет очень низкий уровень удельного сопротивления, но оно не так широко используется из-за его стоимости и из-за того, что оно тускнеет, что может привести к более высокому сопротивлению контактов.
Однако оно используется в некоторых катушках для радиопередатчиков, где низкое удельное электрическое сопротивление серебра снижает потери. При использовании в таких целях серебро обычно наносилось только на существующий медный провод. Покрытие провода серебром позволило значительно снизить затраты по сравнению с цельным серебряным проводом без существенного снижения производительности.
Будет интересно➡ Электромагнитное излучение – невидимый убийца.
Другие материалы в таблице удельного электрического сопротивления могут не иметь такого очевидного применения. Тантал фигурирует в таблице, поскольку используется в конденсаторах — никель и палладий используются в торцевых соединениях многих компонентов поверхностного монтажа, таких как конденсаторы.
Кварц находит свое основное применение в качестве пьезоэлектрического резонансного элемента. Кварцевые кристаллы используются в качестве частотоопределяющих элементов во многих осцилляторах, где высокое значение Q позволяет создавать очень стабильные по частоте схемы. Аналогичным образом они используются в высокоэффективных фильтрах. Кварц имеет очень высокий уровень удельного сопротивления и не является хорошим проводником электричества, то есть его относят к категории диэлектрикам.
Зависимость от температуры
Удельное электрическое сопротивление зависит от температуры. Но все группы веществ проявляют себя по-разному при ее изменении. Это необходимо учитывать при расчете проводов, которые будут работать в определенных условиях. К примеру, на улице, где значения температуры зависят от времени года, необходимые материалы с меньшей подверженностью изменениям в диапазоне от -30 до +30 градусов Цельсия. Если же планируется применение в технике, которая будет работать в одних и тех же условиях, то здесь также нужно оптимизировать проводку под конкретные параметры. Материал всегда подбирается с учетом эксплуатации.
В номинальной таблице удельное электрическое сопротивление берется при температуре 0 градусов Цельсия. Повышение показателей данного параметра при нагреве материала обусловлено тем, что интенсивность передвижения атомов в веществе начинает возрастать. Носители электрических зарядов хаотично рассеиваются во всех направлениях, что приводит к созданию препятствий при передвижении частиц. Величина электрического потока снижается.
При уменьшении температуры условия прохождения тока становятся лучше. При достижении определенной температуры, которая для каждого металла будет отличаться, появляется сверхпроводимость, при которой рассматриваемая характеристика почти достигает нуля.
Отличия в параметрах порой достигают очень больших значений. Те материалы, которые обладают высокими показателями, могут использовать в качестве изоляторов. Они помогают защищать проводку от замыкания и ненамеренного контакта с человеком. Некоторые вещества вообще не применимы для электротехники, если у них высокое значение этого параметра. Этому могут мешать другие свойства. Например, удельная электрическая проводимость воды не будет иметь большого значения для данный сферы. Здесь приведены значения некоторых веществ с высокими показателями.
| Материалы с высоким удельным сопротивлением | ρ (Ом·м) |
| Бакелит | 1016 |
| Бензол | 1015…1016 |
| Бумага | 1015 |
| Вода дистиллированная | 104 |
| Вода морская | 0.3 |
| Дерево сухое | 1012 |
| Земля влажная | 102 |
| Кварцевое стекло | 1016 |
| Керосин | 1011 |
| Мрамор | 108 |
| Парафин | 1015 |
| Парафиновое масло | 1014 |
| Плексиглас | 1013 |
| Полистирол | 1016 |
| Полихлорвинил | 1013 |
| Полиэтилен | 1012 |
| Силиконовое масло | 1013 |
| Слюда | 1014 |
| Стекло | 1011 |
| Трансформаторное масло | 1010 |
| Фарфор | 1014 |
| Шифер | 1014 |
| Эбонит | 1016 |
| Янтарь | 1018 |
Более активно в электротехнике применяются вещества с низкими показателями. Зачастую это металлы, которые служат проводниками. В них также наблюдается много различий. Чтобы узнать удельное электрическое сопротивление меди или других материалов, стоит посмотреть в справочную таблицу.
| Материалы с низким удельным сопротивлением | ρ (Ом·м) |
| Алюминий | 2.7·10-8 |
| Вольфрам | 5.5·10-8 |
| Графит | 8.0·10-6 |
| Железо | 1.0·10-7 |
| Золото | 2.2·10-8 |
| Иридий | 4.74·10-8 |
| Константан | 5.0·10-7 |
| Литая сталь | 1.3·10-7 |
| Магний | 4.4·10-8 |
| Манганин | 4.3·10-7 |
| Медь | 1.72·10-8 |
| Молибден | 5.4·10-8 |
| Нейзильбер | 3.3·10-7 |
| Никель | 8.7·10-8 |
| Нихром | 1.12·10-6 |
| Олово | 1.2·10-7 |
| Платина | 1.07·10-7 |
| Ртуть | 9.6·10-7 |
| Свинец | 2.08·10-7 |
| Серебро | 1.6·10-8 |
| Серый чугун | 1.0·10-6 |
| Угольные щетки | 4.0·10-5 |
| Цинк | 5.9·10-8 |
| Никелин | 0,4·10-6 |
Понятие электрического сопротивления проводника
Классическое определение объясняет электрический ток движением «свободных» (валентных) электронов. Его обеспечивает созданное источником электрическое поле. Перемещение в металле затрудняют не только нормальные компоненты кристаллической решетки, но и дефектные участки, примеси, неоднородные области. В ходе столкновений с препятствиями за счет перехода импульса в тепловую энергию происходит повышение температуры.
Наглядный пример – нагрев воды кипятильником
В газах, электролитах и других материалах несколько отличная физика явления. Линейные зависимости наблюдаются в металлах и других проводниках. Базовые соотношения выражены известной формулой закона Ома:
R (электрическое сопротивление) = U (напряжение)/ I (сила тока).
Для удобства часто используют обратную величину, проводимость (G = 1/R). Она обозначает способность определенного материала пропускать ток с определенными потерями.
Для упрощения иногда применяют пример с водопроводом. Движущаяся жидкость – аналог тока. Давление – эквивалент напряжения. Уменьшением (увеличением) поперечного сечения или положением запорного устройства определяют условия перемещения. Подобным образом изменяют основные параметры электрических цепей с помощью сопротивления (R).
К сведению. Количество жидкости, проходящее за единицу времени через контрольное сечение трубы, – эквивалент электрической мощности.
Величина обратная удельному сопротивлению называется удельной электропроводностью.
c = 1/r = l
/S R = a с z (l+ + l-)
Размерность удельной электропроводности Ом-1 м-1 = См/м (См – сименс)
Удельная электропроводность раствора характеризует электрическую проводимость объема раствора, заключенного между двумя параллельными электродами, имеющими площадь по 1 м и расположенными на расстоянии 1 м друг от друга.
Эквивалентная электропроводность
. Чтобы выделить эффекты ион-ионного взаимодействия, удельную электропроводность c делят на z+n+с, или z-n-с, где
с —
число молей в единице объема:
l = c/z+n+с = c/z-n-с
( z+n+с = z-n-с – это число грамм-эквивалентов в единице объёма,г-экв/м3)
Величина l называется эквивалентной электропроводностью. li [м2 Ом-1/г-экв].
Она представляет собой электропроводность объёма электролита, содержащего 1 г-экв растворённого вещества и находящегося между двумя параллельными электродами на расстоянии 1м друг от друга. Размерность эквивалентной электропроводности м2 Ом-1 = м2 См, тогда концентрация должна быть выражена в моль/м3.
Для бинарного электролита l = c/zс = a с z (l+ + l-)/zc = a (l+ + l-)
В растворах сильных электролитов, для которых a®1 l = l+ + l-
При бесконечном разведении a®1, тогда l0 = l+0 + l-0
Согласно теории Аррениуса l = a l0
U = Er + Eом + Djк + Djа ; Eом=IR
Равновесн электородный потенц.Ур-е Нернста.Стандрт электрод потенц
Наступление равновесия между Ме и раствором его соли характеризуется тем, что устанавливается опред. по величине и направлению скачек потенциала или равновесный потенциал. (мера изменения энергии Гиббса)
Равновесие препятствует дальнейшему окислению и восстановлению, поэтому равновесный потенциал может служить мерой максим. работы процесса который стремится соверш. на электроде.
Ме скорости выравниваются
i=i=iº — ток обмена
— не зависит от активности участников процесса, а опред. лишь природой электрода и раствора.( a=1).Величины
можно измерить на основе ТД данных,является константой.если отриц то металл будет окисл водородом.если положит то не б\т окисляться
Поляризациооные кривые в усл-ях электрохим перенапряжения
рассчит-я по ф-летполяризационная кривая симметр относ-но начала координат при отклонении от 0,5 симметричность нарушается.пунктиром показаны поляризационные кривые,отвеч- щие завимисимости частных плотностей токов в прямом и обратном от потенциала.
h = a + b lg i- уравнение Тафеля. Величины i0 и a можно найти графически (рис), откладывая h против lg i в той области перенапряжений, где справедливо уравнение Тафеля. Наклон b прямой h — lg i равен
и, следовательно
Ток обмена может быть определён по величине перенапряжения при единичной плотности тока, то есть при lg i = 0. Тогда h=а
Рис. Определение тафелевских констант
а
и
b
из полулогарифмических зависимостей перенапряжения от плотности тока
Билет
1диффузия в р-рах электролитов. Изменение концентрации (а точнее активности) растворённого вещества в одной части раствора по отношению к другой приводит к возникновению потока диффузии.
Количественным выражением процессов диффузии являются законы Фика. Первый закон Фика относится к процессам стационарной диффузии и имеет вид
jd = -Di grad ci jd+ = -D+ dc+/dx
поток диффузии, то есть количество частиц, диффундирующих через единичную площадку в единицу времени. Di –коэффициент диффузии частиц i, имеет размерность м2/с, показывает число частиц, про диффундировавших за 1с через поперечное сечение раствора площадью 1м2 при градиенте концентрации равном единице.
Коэффициенты диффузии ионов связаны с подвижностями ионов следующим образом
jd = -Dэфф grad c
В общем случае подвижности катионов и анионов неодинаковы
l+0 ¹ l-0
а следовательно не равны и их коэффициенты диффузии D+ ¹ D-, поэтому при одном и том же градиенте концентрации скорость диффузии положительных и отрицательных ионов различна.
Предположим, что создана граница между двумя растворами с разной концентрацией. Например, раствор NaCl.
Пусть с1>с2. В водном растворе NaCl D+ < D-. При этом условии анионы в начальный момент времени будут перемещаться слева направо (с1 ®с2) Быстрее чем катионы. В результате этого произойдёт пространственное разделение зарядов и возникнет электрическое поле, которое будет ускорять движение катионов и замедлять движение анионов. Следовательно, через короткий промежуток времени скорости перемещения катионов и анионов выровняются. В этих условиях можно говорить об общем потоке электролита. Однако этот поток не является обычным потоком диффузии , так как между двумя областями раствора с концентрациями с1 и с2 устанавливается стационарная разность потенциалов, которая называется диффузионным потенциалом jd.
— эффективный коэффициент диффузии электролита. Термин эффективный отражает то, что в действительности перемещение ионов происходит не только за счёт диффузии, но и под действием электрического поля (миграции).
Величина диффузионного потенциала будет определяться соотношением
2. Скорость электрохимической реакции Электрохимическую реакцию можно рассматривать как гетерогенную химическую реакцию и скорость её подобно скорости любой химической реакции, определяется как количество вещества, изменившееся за единицу времени, то есть
V = ± dDm/dt
Поскольку между количеством прореагировавшего вещества и количеством электричества существует прямая пропорциональность, согласно закону Фарадея, то можно записать
V = ± dDm/dt = k I dt/dt = k I
Скорость электрохимической реакции пропорциональна силе тока. Характерной особенностью всех электрохимических реакций является то, что они совершаются на границе раздела электрод – электролит и поэтому их скорость зависит от величины поверхности раздела. i
= I/S — плотность тока [A/см2].
Если электрохимическая цепь работает как электролизёр, то
U = Er + Djк + Djа + Eом ,
а если – как химический источник тока, то
U = Er — Djк — Djа — Eом
электродную поляризацию (Dj) можно определить, то есть как разность потенциала электрода, через который протекает ток (ji) и его равновесным потенциалом (jr)
Dj = ji — jr
Любой электродный процесс всегда имеет ряд последовательных стадий: сначала реагирующее вещество подходит к электроду, затем происходит собственно электрохимическая стадия, связанная с переносом электронов или ионов через границу раздела фаз (стадия разряда-ионизации
), и, наконец, образовавшиеся продукты реакции должны отойти от поверхности электрода. Первая и третья стадии имеют одинаковые закономерности и называются
стадиями массопереноса
. Стадии массопереноса и разряда-ионизации присутствуют во всех без исключения электродных процессах. Помимо этих стадий при протекании электродных реакций встречаются также и другие. Так электродные процессы могут осложняться химическими реакциями в объёме раствора или на поверхности электрода, в которых может участвовать исходное вещество или продукт электрохимической реакции. Скорость процесса, состоящего из ряда последовательных стадий, определяется скоростью самой медленной стадии, которая называется
лимитирующей
или
контролирующей
Если известна природа лимитирующей стадии то поляризацию заменяем перенапряжением.виды:
Диффузионное перенапряжение возникает при лимитирующей стадии массопереноса;
· Электрохимическое перенапряжение (разряда-ионизации) возникает при лимитирующей стадии разряда — ионизации;
· Фазовое перенапряжение возникает при лимитирующей стадии построения или разрушения кристаллической решётки или зарождения новой фазы (газовой, жидкой, кристаллической);
· Перенапряжение химической реакции возникает при замедленной стадии химической реакции.
3 хим цепи с индивид расплавленными солями и смесями солей.В химических цепях токообразующий процесс связан с взаимодействием чистых компонентов и образованием соответствующей соли.
1) С инд. Расплавленной солью
Это цепь с одной солью в качестве электролита, в которой помещены электроды: металлический и газовый.
Pb|PbCl2|Cl2,C
Е изм будет соответствовать стандартному значению
На границе раздела образуется ДЭС и возникает скачек потенциала. Газовые электроды имеют более + φ чем металлические, следовательно возникает разность φ, а в системе ЭДС
DG0 = — zFЕ0
DS0 = zF
DH0 = DG0 + TDS0 = — zFЕ0 + zFT .
2) Химические цепи с расплавленными солевыми смесями
Pb|PbCl2, LiCl|Cl2,C; Ag|AgI, KI|I2,C
Раствор т/ко Pb как более электроположит , LiCl- фоновый,индифирентный электролит.
Токообразующим процессом является процесс образования МеХ2(PbCl2, AgI) из чистых металла и галогена.
Билет
1.скачки на потенц на границе разд фаз. Электродным потенциалом называют ЭДС электрохимической цепи, в которой слева находится стандартный водородный электрод, потенциал которого условно принят за нуль, а справа — данный электрод.
| М1 |
| L1 |
| L2 |
| М2 |
| М1 |
| ЕЕ |
Е- суммарный эффект скачков потенциала на границах раздела фаз
= mia ± ziFga; – электрохимический потенциал частиц сорта i в фазе a; ga – внутренний потенциал, который представляет собой разность потенциалов между точкой внутри фазы a и бесконечно удалённой точкой в вакууме; zi – заряд частиц сорта i. Условием равновесия для заряженных частиц с фазами a и b будет равенство их электрохимических потенциалов. =
Работа перенесения заряженной частицы из фазы a в фазу b будет равна разности её электрохимических потенциалов в этих фазах, то есть — = (mia — mib) ± ziF(ga — gb)
Электрохимический потенциал частицы i в фазе a равен работе перенесения моля данного компонента i из бесконечности в вакууме внутрь данной фазы.
ga — gb — разность внутренних потенциалов называется гальвани потенциалом и обозначается как gab.В условиях равновесия gab = (mia — mib)/ ziF ЭДС электрохимической системы, которая представляет собой сумму скачков потенциала на границах раздела фаз, является в то же время суммой всех гальвани потенциалов. Е = gМ1L1 + gL1L2 + gL2M2 + gМ2M1
Если в электрохимической системе потенциал gL1L2 отсутствует, то Е = gМ1L1 — g M2L2 — gМ1M2
С другой стороны ЭДС представляет собой разность двух электродных потенциалов, то есть
Е = jп — jл
2. Концентрационные электрохим. цепи Оба электрода идентичны по физическому состоянию и по химической природе. Они отличаются концентрацией компонентов Ox и Red.
Источником электрической энергии является разность свободных энергий Гиббса, обусловленная различными активностями одних и тех же химических компонентов.
Концентрационные цепи можно приготовить следующим образом:
1.Из амальгам разных концентраций в одном и том же растворе;
2.Из одинаковых электродов 1 и 2 рода, находящихся в растворах разной концентрации (активности);
3.Из одинаковых газовых электродов, работающих при разных давлениях.
Различают концентрационные цепи без переноса и с переносом. При работе концентрационных цепей идёт выравнивание активностей или давлений. Cu çZn (Hg)(a1) ç ZnSO4 ç Zn (Hg)(a2) çCu цепь без переноса
Если а1 > а2, то левый электрод – анод, а правый – катод. E = jк — jа = RT/2F ln a1/a2Zn ç ZnSO4 (а’)çç ZnSO4 (a’’)ç Zn
цепь с переносом
Если а’ < а’’, то левый электрод – анод, а правый – катод. E = jк — jа = RT/2F ln a’’/a’ К: Cu2++2e=Cu0 А: Cu0-2e=Cu2+
3. электролиз расплавленных солей широко используется для получения легких, тугоплавких, редких металлов, сплавов, фтора, хлора, для рафинирования металлов. Применение электролиза расплавленных солей весьма перспективно для получения сплавов и соединений, а так же для нанесения гальванических покрытий и обработки поверхности металлов.
· высокая интенсивность процесса, которая может в 25-100 раз превышать интенсивность электролиза водных растворов;
· возможность работы в широком диапазоне температур и концентрацией электролита; значительное сокращение расхода воды.
· значительный удельный расход электроэнергии,
· повышенные капитальные и эксплуатационные затраты на охрану окружающей среды,
В настоящее время считается, что расплавленные соли близки по своему строению к твердому веществу. Расплавленные соли при температурах, близких к температуре плавления, наследуют структуру твердого в-ва. Структура твердого кристалла характеризуется дальним порядком, т.е. правильным расположением частиц одна около другой во всем объеме кристалла.Но имеются разл дефекты.они увел-ся с увел-ем темп-ры,тем самым уменьшают дальний порядок.При переоде в жидкое сост-е дальний порядок полностью нар-ся,но созр ближний порядок.ряд солей имеют молекулярную стр-ру при их нагревании стр-ра сохр,расплав становится непроводящим.Для некоторых солей характерна слоистая стр-ра, в этом случае кристалл состоит из отдел-х пакетов.
Билет
1. ДЭС При соприкосновении двух фаз, имеющих заряженные частицы, возможен переход таких частиц в неэквивалентном количестве из фазы в фазу. При этом в поверхностных слоях каждой из фаз возникают электрические заряды, равные по величине, но противоположные по знаку. Образуется так называемый двойной электрический слой (ДЭС), разность зарядов между обкладками которого, обуславливает скачок потенциала.
Примером может служить поверхность раздела между металлом и водным раствором электролита.
ДЭС может образовываться и без перехода заряженных частиц из фазы в фазу. В этом случае образование ДЭС возможно за счёт избирательной адсорбции ионов одной из фаз на поверхности другой. ДЭС может образоваться при адсорбции и ориентации полярных молекул жидкой фазы (например, воды) на поверхности твёрдого тела.
Ме Меz+ + ze (A) окисление
Ме Меz+ + ze (B) восстановление
Скорости прямого и обратного процессов неодинаковы
Скорость восстановления и окисления можно измерять плотностью тока
реакция А i
реакция B
i
По мере увеличения этих зарядов скорость реакции В будет уменьшаться, а скорость реакции А увеличиваться до наступления равновесия
Температурная зависимость ρ(Т)
Для большинства материалов проведены многочисленные эксперименты по измерению значений удельных сопротивлений. Данные по большинству проводников можно найти в справочных таблицах.
Удельное сопротивление металлов и сплавов, Ом*мм2/м
(при Т = 20С)
| Серебро | 0,016 | Бронза (сплав) | 0,1 |
| Медь | 0,017 | Олово | 0,12 |
| Золото | 0,024 | Сталь (сплав) | 0,12 |
| Алюминий | 0,028 | Свинец | 0,21 |
| Иридий | 0,047 | Никелин (сплав) | 0,42 |
| Молибден | 0,054 | Манганин (сплав) | 0,45 |
| Вольфрам | 0,055 | Константан (сплав) | 0,48 |
| Цинк | 0,06 | Титан | 0,58 |
| Латунь (сплав) | 0,071 | Ртуть | 0,958 |
| Никель | 0,087 | Нихром (сплав) | 1,1 |
| Платина | 0,1 | Висмут | 1,2 |
Чаще всего приводятся значения ρ при нормальной, то есть комнатной температуре 20С. Но оказалось, что при повышении температуры удельное сопротивление возрастает по линейному закону в соответствии с формулой:
$ ρ(Т) = ρ0 * (1 + α*T)$ (6),
где: ρ — удельное сопротивление проводника при температуре 0С, α — температурный коэффициент удельного сопротивления, который тоже имеет для каждого вещества свое, индивидуальное, значение. Из формулы (6) следует, что коэффициент α имеет размерность или .
В соответствии с законом Джоуля-Ленца при протекании электрического тока т выделяется тепло, а значит происходит рост температуры проводника. Кроме этого, в зависимости от области применения, электрические приборы могут работать как при пониженных (минусовых), так и при высоких температурах. Для точных расчетов электрических цепей необходимо учитывать зависимость ρ(Т). Величину α для конкретного материала можно узнать из справочной литературы.
Удельное электрическое сопротивление
Дальнейшие исследования позволили установить связь величины электрического сопротивления с его основными геометрическими размерами. Оказалось, что сопротивление проводника прямо пропорционально длине проводника L и обратно пропорционально площади поперечного сечения проводника S.
Эта функциональная связь хорошо описывается следующей формулой:
$ R = ρ *{ Lover S} $ (4)
Постоянная для каждого вещества величина ρ была названа удельным сопротивлением. Значение этого параметра зависит от плотности вещества, его кристаллической структуры, строения атомов и прочих внутренних характеристик вещества. Из формулы (4) можно получить формулу для расчета удельного сопротивления, если имеются экспериментальные значения для R, L и S:
$ ρ = R*{ Sover L } $ (5)
Для большинства известных веществ измерения были произведены и внесены в справочные таблицы электрических сопротивлений проводников.
Удельное сопротивление металлов, Ом*мм2/м
(при Т = 20С)
| Серебро | 0,016 | Бронза (сплав) | 0,1 |
| Медь | 0,017 | Олово | 0,12 |
| Золото | 0,024 | Сталь (сплав) | 0,12 |
| Алюминий | 0,028 | Свинец | 0,21 |
| Иридий | 0,047 | Никелин (сплав) | 0,42 |
| Молибден | 0,054 | Манганин (сплав) | 0,45 |
| Вольфрам | 0,055 | Константан (сплав) | 0,48 |
| Цинк | 0,06 | Титан | 0,58 |
| Латунь (сплав) | 0,071 | Ртуть | 0,958 |
| Никель | 0,087 | Нихром (сплав) | 1,1 |
| Платина | 0,1 | Висмут | 1,2 |
Экспериментально было обнаружено, что с понижением температуры сопротивление металлов уменьшается. При приближении к температуре абсолютного нуля, которая равна -273С, сопротивление некоторых металлов стремится к нулю. Это явление называется сверхпроводимостью. Атомы и молекулы как бы “замораживаются”, прекращают любое движение и не оказывают сопротивления потоку электронов.
§ 4. Электрическое сопротивление и проводимость
Физическая природа электрического сопротивления.
При движении свободных электронов в проводнике они сталкиваются на своем пути с положительными ионами 2, атомами и молекулами вещества, из которого выполнен проводник, и передают им часть своей энергии. При этом энергия движущихся электронов в результате столкновения их с атомами и молекулами частично выделяется и рассеивается в виде тепла, нагревающего проводник.
Ввиду того, что электроны, сталкиваясь с частицами проводника, преодолевают некоторое сопротивление движению, принято говорить, что проводники обладают электрическим сопротивлением. Если сопротивление проводника мало, он сравнительно слабо нагревается током; если сопротивление велико, проводник может раскалиться.
Провода, подводящие электрический ток к электрической плитке, почти не нагреваются, так как их сопротивление мало, а спираль плитки, обладающая большим сопротивлением, раскаляется докрасна. Еще сильнее нагревается нить электрической лампы.
За единицу сопротивления принят Oм. Сопротивлением 1 Ом обладает проводник, по которому проходит ток 1 А при разности потенциалов на его концах (напряжении), равной 1 В. Эталоном сопротивления 1 Ом служит столбик ртути длиной 106,3 см и площадью поперечного сечения 1 мм2 при температуре 0°С.
На практике часто сопротивления измеряют тысячами Oм — килоомами(кОм) или миллионами Oм — мегаомами (МОм). Сопротивление обозначают буквой R ( r ).
Проводимость.
Всякий проводник можно характеризовать не только его сопротивлением, но и так называемой проводимостью — способностью проводить электрический ток. Проводимость есть величина, обратная сопротивлению.
Единица проводимости называется сименсом (См). 1 См равен 1/1 Ом. Проводимость обозначают буквой G (g). Следовательно,
G = 1 / R (4)
Удельное электрическое сопротивление и проводимость. Атомы разных веществ оказывают прохождению электрического тока неодинаковое сопротивление. О способности отдельных веществ проводить электрический ток можно судить по их удельному электрическому сопротивлению р.
За величину, характеризующую удельное сопротивление, обычно принимают сопротивление куба с ребром 1 м. Удельное электрическое сопротивление измеряют в Ом*м. Для суждения об электропроводности материалов пользуются также понятием удельная электрическая проводимость σ=1/ρ.
Удельная электрическая проводимость измеряется в сименсах на метр (См/м) (проводимость куба с ребром 1м). Часто удельное электрическое сопротивление выражают в ом-сантиметрах (Ом*см), а удельную электрическую проводимость — в сименсах на сантиметр (См/см). При этом 1 Ом*см = 10-2 Ом*м, а 1 См/см = 102 См/м.
Проводниковые материалы применяют, главным образом, в виде проволок, шин или лент, площадь поперечного сечения которых принято выражать в квадратных миллиметрах, а длину — в метрах.
Поэтому для удельного электрического сопротивления подобных материалов и удельной электрической проводимости введены и другие единицы измерения: ρ измеряют в Ом*мм2/м (сопротивление проводника длиной 1 м и площадью поперечного сечения 1 мм2), а σ — в См*м/мм2 (проводимость проводника длиной 1 м и площадью поперечного сечения 1 мм2).
Из металлов наиболее высокой электропроводностью обладают серебро и медь, так как структура их атомов позволяет легко передвигаться свободным электронам, затем следует золото, хром, алюминий, марганец, вольфрам и т. д. Хуже проводят ток железо и сталь.
Чистые металлы всегда проводят электрический ток лучше, чем их сплавы. Поэтому в электротехнике используют преимущественно очень чистую медь, содержащую только 0,05 % примесей. И наоборот, в тех случаях, когда необходим материал с высоким сопротивлением (для различных нагревательных приборов, реостатов и пр.), применяют специальные сплавы: константан, манганин, нихром, фехраль.
Следует отметить, что в технике, кроме металлических проводников, используют и неметаллические. К таким проводникам относится, например, уголь, из которого изготовляют щетки электрических машин, электроды для прожекторов и пр.
Проводниками электрического тока являются толща земли, живые ткани растений, животных и человека. Проводят электрический ток сырое дерево и многие другие изоляционные материалы во влажном состоянии.
Электрическое сопротивление проводника зависит не только от материала проводника, но и его длины l и площади поперечного сечения s. Электрическое сопротивление подобно сопротивлению, оказываемому движению воды в трубе, которое зависит от площади сечения трубы и ее длины.
Сопротивление прямолинейного проводника
R = ρ (l / s) (5)
Если удельное сопротивление ρ выражено в Ом*мм /м, то для того чтобы получить сопротивление проводника в омах, длину его надо подставлять в формулу (5) в метрах, а площадь поперечного сечения — в квадратных миллиметрах.
Зависимость сопротивления от температуры.
Электропроводность всех материалов зависит от их температуры. В металлических проводниках при нагревании размах и скорость колебаний атомов в кристаллической решетке металла увеличиваются, вследствие чего возрастает и сопротивление, которое они оказывают потоку электронов.
При охлаждении происходит обратное явление: беспорядочное колебательное движение атомов в узлах кристаллической решетки уменьшается, сопротивление их потоку электронов понижается и электропроводность проводника возрастает.
В природе, однако, имеются некоторые сплавы: фехраль, константан, манганин и др., у которых в определенном интервале температур электрическое сопротивление меняется сравнительно мало. Подобные сплавы применяют в технике для изготовления различных резисторов, используемых в электроизмерительных приборах и некоторых аппаратах для компенсации влияния температуры на их работу.
О степени изменения сопротивления проводников при изменении температуры судят по так называемому температурному коэффициенту сопротивления а. Этот коэффициент представляет собой относительное приращение сопротивления проводника при увеличении его температуры на 1 °С. В табл. 1 приведены значения температурного коэффициента сопротивления для наиболее применяемых проводниковых материалов.
Сопротивление металлического проводника Rt при любой температуре t
Rt = R0 [ 1 + α (t — t0) ] (6)
где R0— сопротивление проводника при некоторой начальной температуре t0 (обычно при + 20 °С), которое может быть подсчитано по формуле (5);
t— t0 — изменение температуры.
Свойство металлических проводников увеличивать свое сопротивление при нагревании часто используют в современной технике для измерения температуры. Например, при испытаниях тяговых двигателей после ремонта температуру нагрева их обмоток определяют измерением их сопротивления в холодном состоянии и после работы под нагрузкой в течение установленного периода (обычно в течение 1 ч).
Исследуя свойства металлов при глубоком (очень сильном) охлаждении, ученые обнаружили замечательное явление: вблизи абсолютного нуля (— 273,16 °С) некоторые металлы почти полностью утрачивают электрическое сопротивление.
Они становятся идеальными проводниками, способными длительное время пропускать ток по замкнутой цепи без всякого воздействия источника электрической энергии. Это явление названо сверхпроводимостью.
В настоящее время созданы опытные образцы линий электропередачи и электрических машин, в которых используется явление сверхпроводимости. Такие машины имеют значительно меньшие массу и габаритные размеры по сравнению с машинами общего назначения и работают с очень высоким коэффициентом полезного действия.
Линии электропередачи в этом случае можно выполнить из проводов с очень малой площадью поперечного сечения. В перспективе в электротехнике будет все больше и больше использоваться это явление.
Железо как проводник в электротехнике
Железо — самый распространенный в природе и технике металл (после водорода, который металлом тоже является). Он и самый дешевый, и имеет прекрасные прочностные характеристики, поэтому применяется повсюду как основа прочности различных конструкций.
В электротехнике в качестве проводника железо используется в виде стальных гибких проводов там, где нужна физическая прочность и гибкость, а нужное сопротивление может быть достигнуто за счет соответствующего сечения.
Имея таблицу удельных сопротивлений различных металлов и сплавов, можно посчитать сечения проводов, выполненных из разных проводников.
В качестве примера попробуем найти электрически эквивалентное сечение проводников из разных материалов: проволоки медной, вольфрамовой, никелиновой и железной. За исходную возьмем проволоку алюминиевую сечением 2,5 мм.
Нам нужно, чтобы на длине в 1 м сопротивление провода из всех этих металлов равнялось сопротивлению исходной. Сопротивление алюминия на 1 м длины и 2,5 мм сечения будет равно
, где R – сопротивление, ρ – удельное сопротивление металла из таблицы, S – площадь сечения, L – длина.
Подставив исходные значения, получим сопротивление метрового куска провода алюминия в омах.
После этого разрешим формулу относительно S
, будем подставлять значения из таблицы и получать площади сечений для разных металлов.
Итак,
Так как удельное сопротивление в таблице измерено на проводе длиной в 1 м, в микроомах на 1 мм2 сечения, то у нас и получилось оно в микроомах. Чтобы получить его в омах, нужно умножить значение на 10-6. Но число ом с 6 нулями после запятой нам получать совсем не обязательно, так как конечный результат все равно находим в мм2.
- Медь
- Вольфрам
- Никелин
- Железо
Как видим, сопротивление железа достаточно большое, проволока получается толстая.
Будет интересно➡ Что такое омическое сопротивление?
Но существуют материалы, у которых оно еще больше, например, никелин или константан.
Сопротивление провода
Величина сопротивления провода зависит от трех параметров: удельного сопротивления металла, длины и диаметра самого провода. Формула для расчета сопротивления провода:
где: R — сопротивление провода (Ом) ρ — удельное сопротивление металла (Ом.m) L — длина провода (м) А — площадь поперечного сечения провода (м2)
В качестве примера рассмотрим проволочный резистор из нихрома с удельным сопротивлением 1.10×10-6 Ом.м. Проволока имеет длину 1500 мм и диаметр 0,5 мм. На основе этих трех параметров рассчитаем сопротивление провода из нихрома:
R=1,1*10 -6 *(1,5/0,000000196) = 8,4 Ом
Нихром и константан часто используют в качестве материала для сопротивлений. Ниже в таблице вы можете посмотреть удельное сопротивление некоторых наиболее часто используемых металлов.
Почему у металлов самые низкие удельные сопротивления
Из приведенной таблицы видно, что самыми низкими значениями удельных сопротивлений обладают металлы: серебро, медь, золото, алюминий и др. Такое свойство металлов связано с большой концентрацией свободных электронов, “не привязанных” к конкретному атому, а блуждающих в пространстве кристаллической решетки. Напряжение, приложенное к концам проводника, создает электрическое поле, которое действует на электроны, заставляя их двигаться согласованно, в одном направлении.
Рис. 2. Электрический ток в металлах, свободные электроны.
Самым низким значением ρ обладает серебро — 0,016 Ом*мм2/м. Но для повсеместного, массового, использования в сетях электроснабжения и оборудовании этот металл не используется в виду слишком большой цены. Серебро применяется для создания самых ответственных контактов в специальных электротехнических устройствах. В следующей таблице приведены величины удельных сопротивлений металлов и сплавов, часто используемых металлов в электротехнике:
Таблица
Удельные сопротивления металлов, Ом*мм2/м
(при Т = 200С)
| Серебро | 0,016 | Бронза (сплав) | 0,1 |
| Медь | 0,017 | Олово | 0,12 |
| Золото | 0,024 | Сталь (сплав) | 0,12 |
| Алюминий | 0,028 | Свинец | 0,21 |
| Иридий | 0,047 | Никелин (сплав) | 0,42 |
| Молибден | 0,054 | Манганин (сплав) | 0,45 |
| Вольфрам | 0,055 | Константан (сплав) | 0,48 |
| Цинк | 0,06 | Титан | 0,58 |
| Латунь (сплав) | 0,071 | Ртуть | 0,958 |
| Никель | 0,087 | Нихром (сплав) | 1,1 |
| Платина | 0,1 | Висмут | 1,2 |
Наиболее популярными в электротехнике являются медь и алюминий. Медь и медные сплавы применяются для изготовления кабельной продукции и шунтов — деталей, ограничивающих большие токи через измерительные приборы.
Влияние температуры на удельное сопротивление
В справочниках значения ρ металлов приводятся при комнатной температуре 200С. Но эксперименты показали, что зависимость ρ(Т) имеет линейный характер и описывается формулой:
$ ρ(Т) = ρ0 * (1 + α*T)$ (3),
где: ρ0 — удельное сопротивление проводника при температуре 00С, α— температурный коэффициент сопротивления, который тоже имеет тоже индивидуален для каждого вещества. Значения α, полученные опытным путем, можно узнать из справочников. Ниже приведены значения α для некоторых металлов:
- Серебро — 0,0035;
- Медь — 0,004;
- Алюминий — 0,004;
- Железо — 0,0066;
- Платина — 0,0032;
- Вольфрам — 0,0045.
Таким образом, при повышении температуры сопротивление металлов растет. Это объясняется тем, что с ростом температуры увеличивается число дефектов в кристаллической решетке из-за более интенсивных тепловых колебаний ионов, тормозящих электронный ток.
Температурная зависимость удельного сопротивления металлов.
При приближении температуры металла к абсолютному нулю удельное сопротивление резко падает до нуля. Это явление называется сверхпроводимостью, а материалы, обнаруживающие такую способность, называются сверхпроводниками. Этот эффект открыл в 1911 г. голландский физик Камерлинг-Оннес. В его эксперименте удельное сопротивление ртути уменьшилось до нуля при 4,10К.
Использование в электротехнике
Изменение параметра при разных температурах широко применяется в электротехнике. Наиболее простым примером является лампа накаливания, где используется нихромовая нить. При нагревании она начинает светиться. При прохождении через нее тока она начинает нагреваться. С ростом нагрева возрастает и сопротивление. Соответственно, ограничивается первоначальный ток, который нужен был для получения освещения. Нихромовая спираль, используя тот же принцип, может стать регулятором на различных аппаратах.
Широкое применение коснулось и благородных металлов, которые обладают подходящими характеристиками для электротехники. Для ответственных схем, которым требуется быстродействие, подбираются серебряные контакты. Они обладают высокой стоимостью, но с учетом относительно небольшого количества материалов их применение вполне оправданно. Медь уступает серебру по проводимости, но обладает более доступной ценой, благодаря чему ее чаще используют для создания проводов.
В условиях, где можно использовать предельно низкие температуры, применяются сверхпроводники. Для комнатной температуры и уличной эксплуатации они не всегда уместны, так как при повышении температуры их проводимость начнет падать, поэтому для таких условий лидерами остаются алюминий, медь и серебро.
На практике учитывается много параметров и этот является одним из наиболее важных. Все расчеты проводятся еще на стадии проектирования, для чего и используются справочные материалы.
Свойства резистивных материалов
Удельное сопротивление металла зависит от температуры. Их значения приводится, как правило, для комнатной температуры (20°С). Изменение удельного сопротивления в результате изменения температуры характеризуется температурным коэффициентом.
Например, в термисторах (терморезисторах) это свойство используется для измерения температуры. С другой стороны, в точной электронике, это довольно нежелательный эффект. Металлопленочные резисторы имеют отличные свойства температурной стабильности. Это достигается не только за счет низкого удельного сопротивления материала, но и за счет механической конструкции самого резистора.
Много различных материалов и сплавов используются в производстве резисторов. Нихром (сплав никеля и хрома), из-за его высокого удельного сопротивления и устойчивости к окислению при высоких температурах, часто используют в качестве материала для изготовления проволочных резисторов. Недостатком его является то, что его невозможно паять. Константан, еще один популярный материал, легко паяется и имеет более низкий температурный коэффициент.
Материалы высокой проводимости
К наиболее широкораспрстраненным материалам высокой проводимости следует отнести медь и алюминий (Сверхпроводящие материалы, имеющие типичное сопротивление в 10-20 раз ниже обычных проводящих материалов (металлов) рассматриваются в разделе Сверхпроводимость).
Медь
Преимущества меди, обеспечивающие ей широкое применение в качестве проводникового материала, следующие:
- малое удельное сопротивление;
- достаточно высокая механическая прочность;
- удовлетворительная в большинстве случаев применения стойкость по отношению к коррозии;
- хорошая обрабатываемость: медь прокатывается в листы, ленты и протягивается в проволоку, толщина которой может быть доведена до тысячных долей миллиметра;
- относительная легкость пайки и сварки.
Медь получают чаще всего путем переработки сульфидных руд. После ряда плавок руды и обжигов с интенсивным дутьем медь, предназначенная для электротехнических целей, обязательно проходит процесс электролитической очистки.
В качестве проводникового материала чаще всего используется медь марок М1 и М0. Медь марки М1 содержит 99.9% Cu, а в общем количестве примесей (0.1%) кислорода должно быть не более 0,08%. Присутствие в меди кислорода ухудшает ее механические свойства. Лучшими механическими свойствами обладает медь марки М0, в которой содержится не более 0.05% примесей, в том числе не свыше 0.02% кислорода.
Медь является сравнительно дорогим и дефицитным материалом, поэтому она все шире заменяется другими металлами, особенно алюминием.
В отдельных случаях применяются сплавы меди с оловом, кремнием, фосфором, бериллием, хромом, магнием, кадмием. Такие сплавы, носящие название бронз, при правильно подобранном составе имеют значительно более высокие механические свойства, чем чистая медь.
Алюминий
Алюминий является вторым по значению после меди проводниковым материалом. Это важнейший представитель так называемых легких металлов: плотность литого алюминия около 2.6, а прокатанного — 2.7 Мг/м3. Т.о., алюминий примерно в 3.5 раза легче меди. Температурный коэффициент расширения, удельная теплоемкость и теплота плавления алюминия больше, чем меди. Вследствие высоких значений удельной теплоемкости и теплоты плавления для нагрева алюминия до температуры плавления и перевода в расплавленное состояние требуется большая затрата тепла, чем для нагрева и расплавления такого же количества меди, хотя температура плавления алюминия ниже, чем меди.
Алюминий обладает пониженными по сравнению с медью свойствами — как механическими, так и электрическими. При одинаковом сечении и длине электрическое сопротивление алюминиевого провода в 1.63 раза больше, чем медного. Весьма важно, что алюминий менее дефицитен, чем медь.
Для электротехнических целей используют алюминий, содержащий не более 0.5% примесей, марки А1. Еще более чистый алюминий марки АВ00 (не более 0.03% примесей) применяют для изготовления алюминиевой фольги, электродов и корпусов электролитических конденсаторов. Алюминий наивысшей чистоты АВ0000 имеет содержание примесей не более 0ю004%. Добавки Ni, Si, Zn или Fe при содержании их 0.5% снижают γ отожженного алюминия не более, чем на 2-3%. Более заметное действие оказывают примеси Cu, Ag и Mg, при том же массовом содержании снижающие γ алюминия на 5-10%. Очень сильно снижают электропроводность алюминия Ti и Mn.
Алюминий весьма активно окисляется и покрывается тонкой оксидной пленкой с большим электрическим сопротивлением. Эта пленка предохраняет металл от дальнейшей коррозии.
Будет интересно➡ Что такое фазное и линейное напряжение?
Алюминиевые сплавы обладают повышенной механической прочностью. Примером такого сплава является альдрей, содержащий 0.3-0.5% Mg, 0.4-0.7% Si и 0.2-0.3% Fe. В альдрее образуется соединение Mg2Si, которое сообщает высокие механические свойства сплаву.
Железо и сталь
Железо (сталь) как наиболее дешевый и доступный металл, обладающий к тому же высокой механической прочностью, представляет большой интерес для использования в качестве проводникового материала. Однако даже чистое железо имеет значительно более высокое сравнительно с медью и алюминием удельное сопротивление; ρ стали, т.е. железа с примесью углерода и других элементов, еще выше. Обычная сталь обладает малой стойкостью коррозии: даже при нормальной температуре, особенно в условиях повышенной влажности, она быстро ржавеет; при повышении температуры скорость коррозии резко возрастает. Поэтому поверхность стальных проводов должна быть защищена слоем более стойкого материала. Обычно для этой цели применяют покрытие цинком.
В ряде случаев для уменьшения расхода цветных металлов применяют так называемый биметалл. Это сталь, покрытая снаружи слоем меди, причем оба металла соединены друг с другом прочно и непрерывно.
Натрий
Весьма перспективным проводниковым материалом является металлический натрий. Натрий может быть получен электролизом расплавленного хлористого натрия NaCl в практически неограниченных количествах. Из сравнения свойств натрия со свойствами других проводниковых металлов видно, что удельное сопротивление натрия примерно в 2.8 раза больше ρ меди и в 1.7 раз больше ρ алюминия, но благодаря чрезвычайно малой плотности натрия (плотность его почти в 9 раз меньше плотности меди), провод из натрия при данной проводимости на единицу длины должен быть значительно легче, чем провод из любого другого металла. Однако натрий чрезвычайно активен химически (он интенсивно окисляется на воздухе, бурно реагирует с водой), почему натриевый провод должен быть защищен герметизирующей оболочкой. Оболочка должна придавать проводу необходимую механическую прочность, так как натрий весьма мягок и имеет малый предел прочности при деформациях.
Объемное сопротивление
— сопротивление диэлектрика постоянному току при прохождении тока по всему объему материала. Удельное объемное электрическое сопротивление вещества численно равно сопротивлению, которое оказывает постоянному току куб, сделанный из этого вещества, с ребром в единицу длины при условии, что ток проходит через две противоположные грани перпендикулярно к ним. Чем больше удельное объемное электрическое сопротивление материала, тем лучше его электроизоляционные качества. По системе СИ удельное объемное электрическое сопротивление определяют для куба с ребром в 1 метр и выражают его в омометрах — Ом • м. Практически удобно определять удельное объемное электрическое сопротивление для куба с ребром, равным одному сантиметру, и выражать его в омосантиметрах — Ом • см • 1 Ом • м= 100 Ом • см.
Высококачественные диэлектрики имеют удельное объемное электрическое сопротивление от 1015 до Ш20 Ом • см, хорошие — от 10й до 1013 Ом • см. Диэлектрики со значением удельного объемного электрического сопротивления ниже, указанного применяют в установках, не требующих высокой степени изоляции.
Поверхностное сопротивление — сопротивление диэлектрика постоянному току при прохождении тока по его поверхности. Поверхностное сопротивление измеряется в омах.
Необходимо отметить такие свойства диэлектриков, как термопластичность, вязкость, теплостойкость, химическая стойкость и влагостойкость, морозостойкость, тропи^коустойчивость, температура размягчения и др. Важным химическим свойством электроизоляционных материалов является способность склеиваться, растворяться в лаках и растворителях, защищать металлы от коррозии.
К электроизоляционным материалам относятся:
Бумага — волокнистый материал разного цвета. Изготавливается из древесины хвойных пород, хлопка, тростника и асбеста. Выпускается следующих видов: конденсаторная бумага (марки КОН-1 и КОН-2) толщиной от 7 до 30 мкм. Используется в качестве диэлектрика в бумажных конденсаторах; кабельная бумага (марки К-08, К-12 и К-17— цифры указывают толщину в сотых долях миллиметра) применяется для изоляции кабелей. Электрическая прочность 8—10 кВ/мм; телефонная бумага (марки КТН— желтоватого цвета, КТК — красного, КТС — синего, КТЗ — зеленого) применяется для изоляции жил телефонных кабелей и обмоточных проводов марок ПБ и ПББО. Толщина бумаги 0,05 мм. Электрическая прочность 10—12 кВ/мм; пропиточная бумага (марки ИП-50, ИП-63) — для изготовления листового гетинак-са. Толщина бумаги от 0,09 до 0,13 мм; намоточная бумага—для изготовления труб, цилиндров, каркасов катушек трансформаторов и дросселей. Толщина бумаги 0,05 и 0,07 мм; обклеечная бумага применяется для обклейки листов электротехнической стали. Толщина бумаги 0,033 мм. Максимальная рабочая температура бумаг 80—100° С. Ацетилированные бумаги обладают высокой длительной теплостойкостью (до 230° С). Они не горят, не плавятся. Их пробивное напряжение — до 200 кВ/мм. Кварцевые бумаги имеют высокую теплостойкость, примерно до 1090° С. Стеклочешуйчатая бумага — изготавливается из тонких чешуек стекла с разными подложками.
Прессшпан — электрокартон (марки ЭВ, ЭВС, ЭВТ — плотный, ЭМ — мягкий, ЭМТ — тряпичный высококачественный). Выпускается толщиной от 0,1 до 3,5 мм. Применяется для изготовления прокладок, каркасов катушек трансформаторов и дросселей. Удельное объемное сопротивление 1010 Ом • см, электрическая прочность 12 кВ/мм.
Фибра — изготавливается методом прессования из тонкой бумаги, пропитанной раствором хлористого цинка (марки ФТ — техническая, ФЭ — электротехническая). Выпускается толщиной от 0,6 до 5 мм. Обладает высокой механической прочностью, легко обрабатывается. Применяется для изготовления панелей, втулок, шайб и др. Тонкие сорта фибры носят название летероид. Рабочая температура до 100° С. Удельное объемное сопротивление 1010—1012 Ом • см, электрическая прочность 3,5 кВ/мм.
Пряжа хлопчатобумажная и шелковая употребляется для оплетки (чулок) и обмотки проводов в качестве изоляции, для вязки жгутов и т. д. Нитки хлопчатобумажные глянцевые № 00; 0,1 используются для заделки концов изоляции монтажных проводов и кабелей (наложение бандажей) и вязки монтажных проводов в жгуты. Нитки хлопчатобумажные матовые № 10, 20, 30, 40 применяются для наложения бандажей в местах, где не требуется электроизоляция. Иногда бандаж пропитывают клеями или лаками. Нитки шелковые крученые № 13 разноцветные применяются для маркировки проводов. Нитки капроновые и шелк изоляционный применяются в качестве материала для изоляции монтажных проводов и жил кабелей.
Что такое сопротивление медного провода
В металлах ток образуется при появлении электрического поля. Оно «заставляет» двигаться электроны упорядоченно, в одном направлении. Электроны дальних орбит атома, слабо удерживаемые ядром, формируют ток.
Медные провода
При прохождении отрицательных частиц сквозь кристаллическую решетку молекул меди, они сталкиваются с атомами и другими электронами. Возникает препятствие или сопротивление направленному движению частиц.
Для оценки противодействия току была введена величина «электрическое сопротивление» или «электрический импеданс». Обозначается она буквой «R» или «r». Вычисляется сопротивление по формуле Георга Ома: R=, где U — разность потенциалов или напряжение, действующее на участке цепи, I — сила тока.
Понятие сопротивления
Важно! Чем выше значение импеданса металла, тем меньший ток проходит по нему, и именно медные проводники так широко распространены в электротехнике, благодаря этому свойству.
Исходя из формулы Ома, на величину тока влияет приложенное напряжение при постоянном R. Но резистентность медных проводов меняется, в зависимости от их физических характеристик и условий эксплуатации.
Зависимость силы тока от свойств проводников
Вы уже знаете, что сила тока зависит от напряжения. Ведь напряжение является характеристикой электрического поля.
Но в нашем опыте напряжение оставалось постоянным. Значит, сила тока имеет еще одну зависимость.
Сила тока в цепи зависит от свойств проводников, включенных в электрическую цепь.
Что влияет на сопротивление медного провода
Электрический импеданс медного кабеля зависит от нескольких факторов:
- Удельного сопротивления;
- Площади сечения проволоки;
- Длины провода;
- Внешней температуры.
Последним пунктом можно пренебречь в условиях бытового использования кабеля. Заметное изменение импеданса происходит при температурах более 100°C.
Зависимость сопротивления
Удельное сопротивление в системе СИ обозначается буквой ρ. Оно определяется, как величина сопротивления проводника, имеющего сечение 1 м2 и длину 1 м, измеряется в Ом ∙ м2. Такая размерность неудобна в электротехнических расчетах, поэтому часто используется единица измерения Ом ∙ мм2.
Важно! Данный параметр является характеристикой вещества — меди. Он не зависит от формы или площади сечения. Чистота меди, наличие примесей, метод изготовления проволоки, температура проводника — факторы, влияющие на удельное сопротивление.
Зависимость параметра от температуры описывается следующей формулой: ρt= ρ20[1+ α(t−20°C)]. Здесь ρ20— удельное сопротивление меди при 20°C, α— эмпирически найденный коэффициент, от 0°Cдо 100°C для меди имеет значение, равное 0,004 °C-1, t — температура проводника.
Ниже приведена таблица значений ρ для разных металлов при температуре 20°C.
Таблица удельного сопротивления
Согласно таблице, медь имеет низкое удельное сопротивление, ниже только у серебра. Это обуславливает хорошую проводимость металла.
Чем толще провод, тем меньше его резистентность. Зависимость R проводника от сечения называется «обратно пропорциональной».
Важно! При увеличении поперечной площади кабеля, электронам легче проходить сквозь кристаллическую решетку. Поэтому, при увеличении нагрузки и возрастании плотности тока, следует увеличить площадь сечения.
Увеличение длины медного кабеля влечет рост его резистентности. Импеданс прямо пропорционален протяженности провода. Чем длиннее проводник, тем больше атомов встречаются на пути свободных электронов.
Выводы
Последним элементом, влияющим на резистентность меди, является температура среды. Чем она выше, тем большую амплитуду движения имеют атомы кристаллической решетки. Тем самым, они создают дополнительное препятствие для электронов, участвующих в направленном движении.
Важно! Если понизить температуру до абсолютного нуля, имеющего значение 0° Kили -273°C, то будет наблюдаться обратный эффект — явление сверхпроводимости. В этом состоянии вещество имеет нулевое сопротивление.
Температурная корреляция
Сравнение проводимости разных видов стали
Характеристики стали зависят от ее состава и температуры:
- Для углеродистых сплавов сопротивление довольно низкое: оно составляет 0,13-0,2 мкОм/м. Чем выше температура, тем больше значение;
- Низколегированные сплавы имеют более высокое сопротивление — 0,2-0,43 мкОм/м;
- Высоколегированные стали отличаются высоким сопротивлением — 0,3-0,86 мкОм/м;
- Благодаря высокому содержанию хрома сопротивление хромистых нержавеющих сплавов равняется 0,5-0,6 мкОм/м;
- Хромоникелевые аустенитные стали являются нержавеющими и благодаря никелю имеют высокую сопротивляемость — 0,7-0,9 мкОм/м.
Медь стоит на втором месте по степени электропроводимости: она отлично пропускает электрический ток и повсеместно используется при изготовлении проводов. Не реже применяют и алюминий: он слабее меди, но дешевле и легче.
Активное сопротивление проводов, кабелей и линий
Из-за того что переменный ток проходит неравномерно, то при одинаковых условиях тока переменного и постоянного R будет отличаться. Как уже было сказано, стальные электропровода имеют лучшее активное R по сравнению с проводниками из цветных металлов, которые имеют одинаковое R при любой силе тока.
Напротив, активное R электрокабелей из стали всегда зависит от электрического тока, поэтому удельную постоянную проводимость в этом случае никогда не используют. Активное R электрокабеля определяют с помощью формулы: R=l/у*s.
Зависимость показаний амперметра и вольтметра от используемого проводника в цепи
Для начала проведем интересный опыт. Соберем электрическую цепь из источника тока, ключа, амперметра и вольтметра. Также мы будем включать в эту цепь проводники из различных материалов. Они закреплены на специальной панели. К этим же проводникам мы будем параллельно подключать вольтметр (рисунок 1).
Проводники у нас обозначены следующим образом: AB — железная проволока, CD — никелиновая проволока, EF — медная проволока.
Эти проводники имеют одинаковую длину и сечение.
Рисунок 1. Зависимость силы тока от используемого в цепи проводника
Сначала подключим в цепь железную проволоку AB. Зафиксируем показания амперметра и вольтметра после замыкания ключа.
Теперь переключимся на никелиновую проволоку CD. Мы заметим, что сила тока в цепи уменьшилась.
Испробуем третий проводник: медную проволоку EF. Теперь сила тока значительно увеличилась.
Вы не забыли, что в нашем опыте был еще и вольтметр? Мы поочередно подключали его к каждому из проводников.
Каждый раз мы получали одинаковое значение напряжения. Оно не изменялось.