Предельный прогиб металлической балки

10.7.
Вертикальные предельные прогибы элементов конструкций и нагрузки, от которых следует определять прогибы, приведены в табл. 19. Требования к зазорам между смежными элементами приведены в п. 6 рекомендуемого приложения 6.

Вертикальные предельные прогибы fu

Нагрузки для определения вертикальных прогибов

1. Балки крановых путей под мостовые и подвесные краны, управляемые:

с пола, в том числе тельферы (тали)

От одного крана

из кабины при группах режимов работы (по ГОСТ 25546—82):

Физиологические и технологические

2. Балки, фермы, ригели, прогоны, плиты, настилы (включая поперечные ребра плит и настилов):

а) покрытий и перекрытий, открытых для обзора, при пролете l

Постоянные и временные длительные

б) покрытий и перекрытий при наличии перегородок под ними

Принимаются в соответствии с п. 6 рекомендуемого приложения 6

Приводящие к уменьшению зазора между несущими элементами конструкций и перегородками, расположенными под элементами

в) покрытий и перекрытий при наличии на них элементов, подверженных растрескиванию (стяжек, полов, перегородок)

Действующие после выполнения перегородок, полов, стяжек

г) покрытий и перекрытий при наличии тельферов (талей), подвесных кранов, управляемых:

/300 или а

/150 (меньшее из двух)

Временные с учетом нагрузки от одного крана или тельфера (тали) на одном пути

/400 или а

/200 (меньшее из двух)

От одного крана или тельфера (тали) на одном пути

д) перекрытий, подверженных действию:

Физиологические и технологические

перемещаемых грузов, материалов, узлов и элементов оборудования и других подвижных нагрузок (в том числе при безрельсовом напольном транспорте)

0,7 полных нормативных значений временных нагрузок или нагрузки от одного погрузчика (более неблагоприятное из двух)

нагрузок от рельсового транспорта:

От одного состава вагонов (или одной напольной машины) на одном пути

3. Элементы лестниц (марши, площадки, косоуры), балконов, лоджий

Те же, что в поз. 2, а

Определяются в соответствии с п. 10.10

4. Плиты перекрытий, лестничные марши и площадки, прогибу которых не препятствуют смежные элементы

Сосредоточенная нагрузка 1 кН (100 кгс) в середине пролета

5. Перемычки и навесные стеновые панели над оконными и дверными проемами (ригели и прогоны остекления)

Приводящие к уменьшению зазора между несущими элементами и оконным или дверным заполнением, расположенным под элементами

Те же, что в поз. 2, а

Обозначения, принятые в табл. 19:

расчетный пролет элемента конструкции;

— шаг балок или ферм, к которым крепятся подвесные крановые пути.

Примечания: 1. Для консоли вместо l

следует принимать удвоенный ее вылет.

2. Для промежуточных значений l

в поз. 2, а

предельные прогибы следует определять линейной интерполяцией, учитывая требования п. 7 рекомендуемого приложения б.

3. В поз. 2, а

цифры, указанные в скобках, следует принимать при высоте помещений до 6 м включительно.

4. Особенности вычисления прогибов по поз. 2, г

указаны в п. 8 рекомендуемого приложения 6.

5. При ограничении прогибов эстетико-психологическими требованиями допускается пролет l

принимать равным расстоянию между внутренними поверхностями несущих стен (или колонн).

Расстояние (зазор) от верхней точки тележки мостового крана до нижней точки прогнутых несущих конструкций покрытий (или предметов, прикрепленных к ним) должно быть не менее 100 мм.

Прогибы элементов покрытий должны быть такими, чтобы, несмотря на их наличие, был обеспечен уклон кровли не менее 1/200 в одном из направлений (кроме случаев, оговоренных в других нормативных документах).

Предельные прогибы элементов перекрытый (балок, ригелей, плит), лестниц, балконов, лоджий, помещений жилых и общественных зданий, а также бытовых помещений производственных зданий исходя из физиологических требований следует определять по формуле

— ускорение свободного падения;

нормативное значение нагрузки от людей, возбуждающих колебания, принимаемое по табл. 20;

1 —

пониженное нормативное значение нагрузки на перекрытия, принимаемое по табл. 3 и 20;

нормативное значение нагрузки от веса рассчитываемого элемента и опирающихся на него конструкций;

частота приложения нагрузки при ходьбе человека, принимаемая по табл. 20;

— коэффициент, принимаемый по табл. 20.

Предельный прогиб металлической балки — Справочник металлиста

Балка является основным элементом несущей конструкции сооружения. При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.
При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах. Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно.

Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений.

Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.

Виды балок

Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению.

Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента.

Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.

Деревянные

Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.

Для расчета максимального прогиба следует учитывать:

Материал. Различные породы дерева обладают разным показателем прочности, твердости и гибкости.
Форма поперечного сечения и другие геометрические характеристики.
Различные виды нагрузки на материал.

Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.

Конструкции из древесины хвойных пород

Стальные

Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.

Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:

электросварка;
заклепки;
болты, винты и другие виды резьбовых соединений.

Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.

Для проведения расчета балки на прогиб может помочь видео:

Прочность и жесткость балки

Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.

Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали. Расчет конструкции по опытным формулам не всегда эффективен.

Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности.

Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.

Существует два основных метода расчета прочности и жесткости:

Простой. При использовании данного метода применяется увеличительный коэффициент.
Точный. Данный метод включает в себя использование не только коэффициентов для запаса прочности, но и дополнительные вычисления пограничного состояния.

Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.

Расчет на жесткость

Для расчета прочности балки на изгиб применяется формула:

Где:

M – максимальный момент, который возникает в балке;

Wn,min – момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.

Ry является расчетным сопротивлением стали при изгибе. Зависит от вида стали.

γc представляет собой коэффициент условий работы, который является табличной величиной.

Расчет жесткости или величины прогиба балки является достаточно простым, поэтому расчеты может выполнить даже неопытный строитель. Однако для точного определения максимального прогиба необходимо выполнить следующие действия:

Составление расчетной схемы объекта.
Расчет размеров балки и ее сечения.
Вычисление максимальной нагрузки, которая воздействует на балку.
Определение точки приложения максимальной нагрузки.
Дополнительно балка может быть проверена на прочность по максимальному изгибающему моменту.
Вычисление значения жесткости или максимально прогиба балки.

Чтобы составить расчетную схему, потребуются такие данные:

размеры балки, длину консолей и пролет между ними;
размер и форму поперечного сечения;
особенности нагрузки на конструкцию и точно ее приложения;
материал и его свойства.

Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.

Расчет моментов инерции и сопротивления сечения

Для выполнения расчетов жесткости потребуется значение момент инерции сечения (J) и момента сопротивления (W). Для расчета момента сопротивления сечения лучше всего воспользоваться формулой:

Важной характеристикой при определении момента инерции и сопротивления сечения является ориентация сечения в плоскости разреза. При увеличении момента инерции увеличивается и показатель жесткости.

Определение максимальной нагрузки и прогиба

Для точного определения прогиба балки, лучше всего применять данную формулу:

Где:

q является равномерно-распределенной нагрузкой;

E – модуль упругости, который является табличной величиной;

l – длина;

I – момент инерции сечения.

Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.

Особенности расчета на прогиб

Расчет на прогиб проводится обязательно для любых перекрытий. Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:

Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.
Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.
Варианты нагружения консольного стержня, который закреплен жестко.
Действие на конструкцию сложной нагрузки.

Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.

Пример подсчета прогиба

Чтобы понять процесс расчета жесткости балки и ее максимального прогиба, можно использовать простой пример проведения расчетов. Данный расчет проводится для балки с такими характеристиками:

материал изготовления – древесина;
плотность составляет 600 кг/м3;
длина составляет 4 м;
сечение материала составляет 150*200 мм;
масса перекрывающих элементов составляет 60 кг/м²;
максимальная нагрузка конструкции составляет 249 кг/м;
упругость материала составляет 100 000 кгс/ м²;
J равно 10 кг*м².

Для вычисления максимальной допустимой нагрузки учитывается вес балки, перекрытий и опор. Рекомендуется также учесть вес мебели, приборов, отделки, людей и других тяжелых вещей, который также будут оказывать воздействие на конструкцию. Для расчета потребуются такие данные:

вес одного метра балки;
вес м2 перекрытия;
расстояние, которое оставляется между балками;
временная нагрузка;
нагрузка от перегородок на перекрытие.

Чтобы упросить расчет данного примера, можно принять массу перекрытия за 60 кг/м², нагрузку на каждое перекрытие за 250 кг/м², нагрузки на перегородки 75 кг/м², а вес метра балки равным 18 кг. При расстоянии между балками в 60 см, коэффициент k будет равен 0,6.

Если подставить все эти значения в формулу, то получится:

q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

Для расчета изгибающего момента следует воспользоваться формулой f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦].

Подставив в нее данные, получается f = (5 / 384) * [(qn * L4) / (E * J)] = (5 / 384) * [(249 * 44) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

Именно это и является показателем прогиба при воздействии на балку максимальной нагрузки. Данные расчеты показывают, что при действии на нее максимальной нагрузки, она прогнется на 0,83 см. Если данный показатель меньше 1, то ее использование при указанных нагрузках допускается.

Использование таких вычислений является универсальным способом вычисления жесткости конструкции и величины их прогибания. Самостоятельно вычислить данные величины достаточно легко. Достаточно знать необходимые формулы, а также высчитать величины. Некоторые данные необходимо взять в таблице.

Варианты перекрытия для разных помещений

В зависимости от типа помещения деревянные перекрытия могут иметь разное строение. Всего возможно три варианта:

для цокольных перекрытий, где характерна разность температур и повышенная влажность, требуется применение пароизоляции, повышенного слоя теплоизоляции и специальной отражающей плёнки или фольги;
для межэтажных перекрытий, которым свойственна более простая структура, в связи с равномерным температурным режимом и стабильным уровнем влажности обязательно необходима шумоизоляция;
для чердачных перекрытий, если они не отапливаются, используется такое же наполнение, как и для цокольных, с тем отличием, что расположение изоляторов происходит в обратном порядке из-за направления действия холода.

Более подробно о строении разных перекрытий будет написано ниже.

Проверка прогибов стальной балки

При расчете стальных балок по II-й ГПС (по прогибам) необходимо создавать раскрепления для прогибов:

Информация из справки LIRA SAPR (СправкаПояснения СтальПроверки прогибов):

Проверка прогиба осуществляется сопоставлением реально определенного относительного прогиба (L/f) с максимально возможным для данного конструктивного элемента прогибом.

В данной версии проверка выполняется только для балок на основании состава загружений во всех сочетаниях. Учитываются коэффициенты надежности по нагрузке (заданные при формировании РСУ в среде ПК ЛИРА-САПР) и коэффициенты сочетания.

Перемещения, вызванные загружениями с долей длительности 0, в данном расчете не используются.

Прогибы находятся для каждого сечения на основании распределения MY1, MZ1, QY1, QZ1 по длине элемента. Соответственно, увеличение количества расчетных сечений способствует более точному определению прогибов (особенно, если воздействуют сосредоточенные силовые факторы).

В режиме локального расчета элемента (см. справочную систему СТК-САПР) имеется возможность расчета прогибов по огибающим эпюрам изгибающего момента в запас. Это может потребоваться, когда редактируются расчетные сочетания усилий (или нагрузок) и теряется связь с результатами расчета на ПК ЛИРА-САПР основной схемы.

Важно: Предусмотрена возможность определять не чистые перемещения (относительно локальных осей Y и Z в недеформированной схеме), а прогиб относительно двух выбранных условно неподвижных точек – точек раскрепления (в случае консоли, например, относительно одной точки).

Схема к определению прогибов балки с раскреплениями и без раскреплений

На приведенном фрагменте показан механизм определения прогибов (они обозначены как di и dk) в конструктивном элементе с наложенными раскреплениями на элементы.

Если раскрепления не наложены, то прогиб принимается равным полному расстоянию до оси X.

Важно: Если балка (ригель) разбита по длине промежуточными узлами, то для нее необходимо создать конструктивный элемент и раскрепления для проверки прогибов создавать как для конструктивного элемента (т.е. для балки как единого целого).

В расчете стальных конструкций коэффициент расчетной длины (и для балок, и для колонн, и для ферм) применяется к длине конечного элемента (КЭ), если не задан конструктивный элемент (КоЭ).

Если задан КоЭ, то коэффициент расчетной длины применяется к полной длине КоЭ.

Расчётная модель рамы с цельным ригелем и разбитым на отдельные элементы

Согласно нормативной документации прогиб определяется от действия нормативных нагрузок. Поскольку в LIRA SAPR все нагрузки прикладываются к узлам и элементам их расчётными значениями, при определении прогибов программа определяет нормативное значение нагрузок путём деления их на коэффициент надёжности.

Посмотреть какие приняты коэффициенты надёжности, а также ввести их вручную, если это необходимо, можно в окне параметров расчёта.

Окно параметров расчёта, вызываемое из окна задания параметров для стальных конструкций

Подробнее о корректировке коэффициентов надёжности для расчета прогибов вручную читайте в статье «Коэффициенты к временным нагрузкам при проверке прогиба»

Мозаика результатов проверки назначенных сечений по 2 предельному состоянию

Предельно допустимый L/200=6000/200=30мм

Без задания раскреплений (по абсолютному перемещению узлов балки): ((39,8мм/ к-т надежности по нагрузке)/ 30мм))*100%=((39,8/1,1)/30)*100%=120,6%

С заданием раскреплений (по относительному перемещению узлов балки за вычетом перемещений опорных узлов): ((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/30)*100%=92,9%

Ручной ввод расчётной длины балки для расчёта прогибов

В диалоговом окне задания характеристик расчёта стальной балки присутствует группа параметров Расчёт по прогибу.

Информация из справки ЛИРА САПР: Расчет по прогибу – данные для расчета прогиба. Длина пролета авто – вычисляется по положению раскреплений. Длина пролета точно – длина пролета при расчете приравнивается этому числу.

Рассмотрим раму из предыдущего примера, только теперь раскрепления для прогибов назначим для всех конструкций, а расчётные длины будем для первого случая задавать автоматическим способом, а для второго ручным.

Расчётная модель с информацией о назначенных расчётных длинах балок

Результаты расчётов прогибов балок

Предельно допустимый прогиб при длине 6 м L/200=6000/200=30мм

Предельно допустимый прогиб при длине 4 м L/200=4000/200=20мм

Проценты использования по предельному прогибу

Длина балки 6 м: ((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/30)*100%=92,9%

Длина балки 4 м: ((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/20)*100%=139,4%

Расчёт прогибов стрельчатой арки

Пример — рама переменного сечения (РПС) пролётом 18 м. Соединение полурам в коньке — шарнирное, опирание полурам на фундамент — шарнирное.

Расчётная модель рамы

При этом в параметрах «Дополнительные характеристики» необходимо указать вручную пролет, с которым программа будет сравнивать прогиб (автоматическое определение пролета возможно только для линейных балок, где все конечные элементы (КЭ) конструктивного элемента (КоЭ) лежат на одной оси):

Эпюра перемещений fz ригеля одной полурамы (вдоль местной оси Z1 стержня)

Мозаика перемещений узлов по Z и «Раскрепления для прогибов» (раскреплён только ригель №4)

Результаты определения прогибов в СТК-САПР:

Результаты определения прогибов ригелей №2 и №4

Предельно допустимый L/200=17664/200=88.32 мм

Без задания раскреплений (по абсолютному значению на эпюре прогибов fz): 96.7/17644=1/182 — совпадает с результатом расчёта элемента №2

С заданием раскреплений (по относительному значению на эпюре прогибов fz): (96.7-(-6.46))/17644=1/171 — совпадает с результатом расчёта элемента №4

Без задания раскреплений (по абсолютному значению перемещений узлов): 99.8/17644=1/177 — не совпадает ни с чем

Вывод: Расчёт на прогибы выполняется в местной системе координат стержня. Прогиб стрельчатых и цилиндрических арок, а также любых криволинейных конструкций, нужно определять по перемещениям узлов в глобальной системе координат и вручную сравнивать с предельно допустимыми значениями.

Пример – цилиндрическая арка пролётом 18 м, стрелой подъёма f = 9 м. Соединение всех элементов между собой — жёсткое, опирание на фундамент — шарнирное.

Нагрузки на арку приложены их расчётными значениями. Значения нагрузок для определения прогибов принимаются согласно СП 20.13330.2016 Нагрузки и воздействия, таблица Д.1 Приложения Д.

В данном примере арка является конструкцией покрытия, прогиб которой должен определяться от постоянных и длительных нагрузок (п.2 табл. Д.1). Для визуализации перемещений от нормативных значений нагрузок, необходимо создать особое РСН с нормативными длительными значениями нагрузок.

Нагрузки в данном РСН нужно поделить на коэффициент надёжности, с учётом длительности. На конструкцию действуют два загружения:

Загружение 1 — постоянное, коэффициент надёжности 1.1; Загружение 2 — кратковременное, коэффициент надёжности 1.2, доля длительности 0.35;

Вычислим коэффициенты для перехода к нормативным значениям

Загружение 1 Kn=1/1.1=0.91; Загружение 2 Kn=1/1.2*0.35=0.292

Таблица РСН с сочетаниями расчётных и нормативных значений нагрузок с учётом длительности.

Мозаика перемещений узлов цилиндрической арки от РСН2

Предельно допустимый прогиб L/200=18000/200=90 мм

Фактический прогиб (по абсолютному значению перемещений узлов): 32.2/18000=1/559 – меньше предельно допустимого значения.

Примечание: если подобная конструкция стоит на своих опорах, то перемещения опорных точек (для получения относительных перемещений) удобно получить через «Мозаику относительных перемещений», указав реперный узел.

Мозаика перемещений узлов в глобальной СК (абсолютных)

Мозаика перемещений узлов в глобальной СК относительно реперного узла

Основы вычислений

Для начала следует понять, что именно требуется рассчитать. Дело в том, что деревянный брус или доска балки под нагрузкой способно изогнуться до определенного предела – эта величина называется пределом прочности – и при дальнейшем увеличении нагрузки сломаться. Под действием нагрузки изогнувшаяся балка может также выскользнуть из креплений. Чтобы избежать этого или хотя бы снизить риск такой неприятности, деревянные балки стараются заделать в кладку дома или прикрепить с помощью кронштейнов, уголков и других видов деталей к деревянной стене дома. Используют также врубку балки в венец стены. Все такие виды фиксации считаются жесткой заделкой.

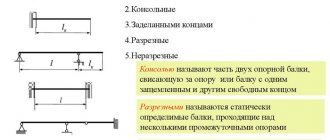
Вот так примерно выглядит расчетная схема для однопролетной балки, то есть изделие, у которого закреплены только концы. Здесь L – пролет балки, расстояние между опорными точками, Q – распределенная нагрузка, f – величина прогиба.

Основой для расчета предельно допустимого прогиба, как и источником других данных о работе деревянных конструкций, является СП 64.13330.2011. Согласно этому документу, предельный прогиб балки для межэтажных перекрытий не должен превышать 1/250 часть длины пролета.

То есть для балки с длиной 6 м допустимый прогиб составит 24 мм. Если же брать более строгие значения (для штукатурки на потолке и требующих строгой плоскости пола второго этажа напольных покрытий, например, плитки) – 1/350, допустимый прогиб уменьшается до 17 мм.

В целом для вычислений используют формулу f=L/350, при этом длину пролета указывают в миллиметрах.

Таблица 1.1. Допустимый прогиб деревянных конструкций.

Соответственно, при расчете балки на прочность в онлайн-калькуляторе или вручную следует уменьшать сечение только до тех пределов прогиба, которые меньше вычисленного значения.

На иллюстрации выше показана расчетная схема для распределенной нагрузки, то есть такой, которая равномерно распределяется по всей балке. Обычно в жилых помещениях используется именно эта схема. Однако при размещении в комнате мебели или оборудования большого веса, особенно не возле стены (на которую опирается край балки), а на некотором удалении от нее, иногда бывает разумнее использовать схему расчета для сосредоточенной нагрузки.

Вот так примерно создается сосредоточенная нагрузка на балку.

Таблица 1.2. Схемы расчета деревянных балок с одной сосредоточенной нагрузкой.

Здесь и далее Е – модуль упругости древесины Е=100 000 кгс/м2), I – осевой момент инерции балки.

Таблица 1.3. Схемы расчета деревянных балок с двумя сосредоточенными нагрузками.

Таблица 1.4. Расчет балки с двусторонним жестким защемлением при равномерно-распределенной нагрузке.

В зависимости от того, куда именно приложены нагрузки и в каком количестве, используется расчетная схема соответствующего типа.

Для бруса, защемленного в стене только одним концом (консольное крепление), используются другие формулы расчета деревянной балки на прочность. Обычно такие вычисления нужны при проектировании навесов на деревянных балках-опорах, больших вылетов крыши и других подобных случаях.

Таблица 1.5. Расчет консольной балки при одной сосредоточенной нагрузке.

Таблица 1.6. Расчет консольной балки при одной неравномерно-распределенной нагрузке.

Таблица 1.7. Расчет консольной балки при одной равномерно-распределенной нагрузке.

Формулы кажутся громоздкими и сложными, но фактически обычному пользователю при расчете деревянных балок перекрытия важно просто представлять себе характер распределения действующих на балку сил и понимать – чтобы соблюсти условия прочности, необходимо правильно выбрать схему приложения нагрузок

Допустимый прогиб металлической балки

Балка – элемент в инженерии, представляющий собой стержень, который нагружают силы, действующие в направлении, перпендикулярном стержню. Деятельность инженеров зачастую включает в себя необходимость расчета прогиба балки под нагрузкой. Этой действие выполняется для того, чтобы ограничить максимальный прогиб балки.

Типы

На сегодняшний день в строительстве могут использоваться балки, изготовленные из разных материалов. Это может быть металл или дерево. Каждый конкретный случай подразумевает под собой разные балки. При этом расчет балок на прогиб может иметь некоторые отличия, которые возникают по принципу разницы в строении и используемых материалов.

Деревянные балки

Сегодняшнее индивидуальное строительство подразумевает под собой широкое применение балок, изготовленных из дерева. Практически каждое строение содержит в себе деревянные перекрытия. Балки из дерева могут использоваться как несущие элементы, их применяют при изготовлении полов, а также в качестве опор для перекрытий между этажами.

Ни для кого не секрет, что деревянная, так же как и стальная балка, имеет свойство прогибаться под воздействием нагрузочных сил. Стрелка прогиба зависит от того, какой материал используется, геометрических характеристик конструкции, в которой используется балка, и характера нагрузок.

Допустимый прогиб балки формируется из двух факторов:

Соответствие прогиба и допустимых значений.
Возможность эксплуатации здания с учетом прогиба.

Проводимые при строительстве расчеты на прочность и жесткость позволяют максимально эффективно оценить то, какие нагрузки сможет выдерживать здание в ходе эксплуатации.

Также эти расчеты позволяют узнать, какой именно будет деформация элементов конструкции в каждом конкретном случае.

Пожалуй, никто не будет спорить с тем, что подробные и максимально точные расчеты – это часть обязанностей инженеров-строителей, однако с использованием нескольких формул и навыка математических вычислений можно рассчитать все необходимые величины самостоятельно.

Для того чтобы произвести правильный расчет прогиба балки, нужно также брать во внимание тот факт, что в строительстве понятия жесткости и прочности являются неразрывными. Опираясь на данные расчета прочности, можно приступать к дальнейшим расчетам относительно жесткости. Стоит отметить, что расчет прогиба балки – один из незаменимых элементов расчета жесткости.

Обратите ваше внимание на то, что для проведения таких вычислений самостоятельно лучше всего использовать укрупненные расчеты, прибегая при этом к достаточно простым схемам. При этом также рекомендуется делать небольшой запас в большую сторону. Особенно если расчет касается несущих элементов.

Расчет балок на прогиб. Алгоритм работы

На самом деле алгоритм, по которому делается подобный расчет, достаточно прост. В качестве примера рассмотрим несколько упрощенную схему проведения расчета, при этом опустив некоторые специфические термины и формулы. Для того чтобы произвести расчет балок на прогиб, необходимо выполнить ряд действий в определенном порядке. Алгоритм проведения расчетов следующий:

Составляется расчетная схема.
Определяются геометрические характеристики балки.
Вычисляется максимальную нагрузку на данный элемент.
В случае возникновения необходимости проверяется прочность бруса по изгибающему моменту.
Производится вычисление максимального прогиба.

Как видите, все действия достаточно просты и вполне выполнимы.

Составление расчетной схемы балки

Для того чтобы составить расчетную схему, не требуется больших знаний. Для этого достаточно знать размер и форму поперечного сечения элемента, пролет между опорами и способ опирания. Пролетом является расстояние между двумя опорами. К примеру, вы используете балки как опорные брусья перекрытия для несущих стен дома, между которыми 4 м, то величина пролета будет равна 4 м.

Вычисляя прогиб деревянной балки, их считают свободно опертыми элементами конструкции. В случае балки перекрытия для расчета принимается схема с нагрузкой, которая распределена равномерно.

Обозначается она символом q. Если же нагрузка несет сосредоточенный характер, то берется схема с сосредоточенной нагрузкой, обозначаемой F.

Величина этой нагрузки равна весу, который будет оказывать давление на конструкцию.

Момент инерции

Геометрическая характеристика, которая получила название момент инерции, важна при проведении расчетов на прогиб балки. Формула позволяет вычислить эту величину, мы приведем ее немного ниже.

При вычислении момента инерции нужно обращать внимание на то, что размер этой характеристики зависит от того, какова ориентация элемента в пространстве. При этом наблюдается обратно пропорциональная зависимость между моментом инерции и величиной прогиба.

Чем меньше значение момента инерции, тем больше будет значение прогиба и наоборот. Эту зависимость достаточно легко отследить на практике.

Каждый человек знает, что доска, положенная на ребро, прогибается гораздо меньше, чем аналогичная доска, находящаяся в нормальном положении.

Подсчет момента инерции для балки с прямоугольным сечением производится по формуле:

J=b*h3/12, где:

b – ширина сечения;

h – высота сечения балки.

Вычисления максимального уровня нагрузки

Определение максимальной нагрузки на элемент конструкции производится с учетом целого ряда факторов и показателей.

Обычно при вычислении уровня нагрузки берут во внимание вес 1 погонного метра балки, вес 1 квадратного метра перекрытия, нагрузку на перекрытие временного характера и нагрузку от перегородок на 1 квадратный метр перекрытия. Также учитывается расстояние между балками, измеренное в метрах.

Для примера вычисления максимальной нагрузки на деревянную балку примем усредненные значения, согласно которым вес перекрытия составляет 60 кг/м², временная нагрузка на перекрытие равна 250 кг/м², перегородки будут весить 75 кг/м². Вес самой балки очень просто вычислить, зная ее объем и плотность. Предположим, что используется деревянная балка сечением 0,15х0,2 м. В этом случае ее вес будет составлять 18 кг/пог.м.

Также для примера примем расстояние между брусьями перекрытия равным 600 мм. В этом случае нужный нам коэффициент составит 0,6.

В результате вычисления максимальной нагрузки получаем следующий результат: q=(60+250+75)*0,6+18=249 кг/м.

Когда значение получено, можно переходить к расчету максимального прогиба.

Вычисление значения максимального прогиба

Когда проводится расчет балки, формула отображает в себе все необходимые элементы. При этом стоит учитывать, что формула, используемая для расчетов, может иметь несколько иной вид, если расчет проводится для разных типов нагрузок, которые будут оказывать влияние на балку.

Сначала приведем вашему вниманию формулу, используемую для расчета максимального прогиба деревянной балки с распределенной нагрузкой.

f=-5*q*l4/384*E*J.

Обратите внимание, что в данной формуле Е – это постоянная величина, которая получила название модуль упругости материала. Для древесины эта величина равна 100 000 кгс/ м².

f=-F*l3/48*E*J, где:

F – сила давления на брус.

Также обращаем внимание на то, что значение модуля упругости, используемое в расчетах, может различаться для разных видов древесины. Влияние оказывают не только порода дерева, но и вид бруса. Поэтому цельная балка из дерева, клееный брус или оцилиндрованное бревно будут иметь разные модули упругости, а значит, и разные значения максимального прогиба.

Вы можете преследовать разные цели, совершая расчет балок на прогиб. Если вы хотите узнать пределы деформации элементов конструкции, то по завершении расчета стрелки прогиба вы можете остановиться. Если же ваша цель – установить уровень соответствия найденных показателей строительным нормам, то их нужно сравнить с данными, которые размещены в специальных документах нормативного характера.

Двутавровая балка

Обратите внимание на то, что балки из двутавра применяются несколько реже в силу их формы. Однако также не стоит забывать, что такой элемент конструкции выдерживает гораздо большие нагрузки, чем уголок или швеллер, альтернативой которых может стать двутавровая балка.

Формулы для расчета прогиба балки

Как построить деревянный дом. Все документы

Фундамент деревянного дома

Гидроизоляция дома современными материалами Гидроизоляция фундамента дома из бревна «дедовским» способом Цоколь, забирка, отмостка Устройство подвала в доме из бревна Материалы и растворы для фундаментов и цоколей Свайные и плитные фундаменты Ленточные фундаменты под дом из бревна Фундаменты столбчатые: деревянные (стулья) и каменные Фундаменты столбчатые из ж/б столбов; технология ТИСЭ Подготовка участка под фундамент Расчет фундаментов деревянного дома

Стены деревянного дома

Общее представление о возведении стен из бревна Принцип рубки стен Рубка углов стен «в обло» или «в чашу» Рубка в «лапу» Стены из бруса Узлы соединений стен из бруса Брус профилированный и клееный Другие варианты угловых врубок Рубка оконных венцов Сруб из оцилиндрованных бревен Стены с вертикальными брусьями; из деревянных кирпичей Конопатные работы Укрепление длинных стен Постановка сруба на место Ремонт стен бревенчатых и брусчатых домов Перегородки в деревянном доме

Окна, двери, лестницы

Клееные конструкции окон Изготовление, установка оконных коробок Изготовление оконных переплетов Сборка окон на винтовых стяжках Изготовление простых щитовых дверей Изготовление филенчатых дверей Дверная коробка, обналичка дверей Крыльцо деревянного дома Терраса деревянного дома Веранда, балкон деревянного дома Основные требования по возведению лестниц Приемы сборки деревянных лестниц Сборка деревянной лестницы

Расчет уклона крыши дома Варианты стропил Соединение стропил Расчет стропил; деревянные карнизы Требования к обрешетке Глиносоломенная (глинокамышовая) кровля Кровля из щепы Кровля из теса в деревянном доме Кровля из шифера (волнистых асбестоцементных листов) Требования к дымоходам

Инструменты, приемы работ

Основной плотницкий инструмент и подготовка его к работе Крепление, перерубка и отеска бревен; врубка в полдерева Разметка бруса; выборка четверти, пазов в бревнах Приемы наращивания, сращивания и соединения бревен Пиление, строгание, сверление Верстак; склеивание древесины

Заготовка, хранение и антисептирование лесоматериалов Фанера, разные древесные плиты Обрезные пиломатериалы из 1м3 бревен; как распилить бревно Выбор бревна; как определить объем одного бревна Свойства древесины – что стоит учесть О древесине и ее породах в строительстве деревянного дома Как устроить теплоизоляцию деревянного дома Особенности участка: грунт и уровень грунтовых вод Какой дом комфортнее: большой или маленький Влияние климатической зоны и поры года на строительство дома Чем руководствоваться при планировке дома

Формулы для расчета прогиба балки

При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах. Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно.

Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.

Общая информация по методологии расчёта

В большинстве случаев в малоэтажном строительстве применяются однопролётные балки.

Они могут быть в виде брёвен, досок или брусьев. Длина элементов может варьироваться в большом диапазоне. В большинстве случаев она напрямую зависит от параметров строения, которые вы собираетесь возвести.

Внимание! Представленный в конце странички калькулятор расчета балок на прогиб позволит вам просчитать все значения с минимальными затратами времени. Чтобы воспользоваться программой, достаточно ввести базовые данные

Роль несущих элементов в конструкции выполняют деревянные бруски, высота сечения которых составляет от 140 до 250 мм, толщина лежит в диапазоне 55—155 мм. Это наиболее часто используемые параметры при расчёте несущей способности деревянных балок.

Очень часто профессиональные строители для того чтобы усилить конструкцию используют перекрёстную схему монтажа балок. Именно эта методика даёт наилучший результат при минимальных затратах времени и материалов.

Если рассматривать длину оптимального пролёта при расчёте несущей способности деревянных балок, то лучше всего ограничить фантазию архитектора в диапазоне от двух с половиной до четырёх метров.

Внимание! Лучшим сечением для деревянных балок считается площадь, у которой высота и ширина соотносятся как 1,5 к 1

для прямоугольных в плане зданий

а) Для стен прямоугольных в плане зданий пиковое положительное значение аэродинамического коэффициента сp

,
+=
1,2.

б) Пиковые значения отрицательного аэродинамического коэффициента сp

,
–
для стен и плоских покрытий (рисунок Д.24) приведены в таблице Д.12.

Т а б л и ц а Д.12

Участок	A	B	C	D	E
cp ,–	–2,2	–1,2	–3,4	–2,4	–1,5

ISOPROMAT.ru

Произвести полный расчет на прочность и проверить жесткость статически определимой двутавровой двухопорной балки (рис. 1) при следующих данных: F=40кН, q=30 кН/м, a=0,8 м, l=4м, допустимые нормальные и касательные напряжения: [ σ ]=160 МПа и [ τ ]=100 МПа, допустимый прогиб балки [f]= l/400

Подготовка расчетной схемы к решению задачи:

Определение опорных реакций

Подробно, пример определения опорных реакций для балки рассмотрен здесь

А также в нашем коротком видеоуроке:

Построение эпюр Q и М

Видео про расчет значений Q и M для построения эпюр:

По этим данным построены эпюры Q и М.

Короткое видео о том, как надо строить эпюры:

Подбор сечения двутавровой балки

Так как Мmах = 45 кНм, то

По сортаменту выбираем двутавр № 24, для которого Wx = 289 см 3 , Ix= 3460 см 4 , Smax = 163 см 3 , h = 24 см, bп = 11,5 см, t = 0,95 см, d = bc = 0,56 см, h = h-2t = 22,1 см.

Этот двутавр будет работать при максимальном нормальном напряжении в крайнем волокне опасного сечения.

Проверка сечения балки по касательным напряжениям

Так как Qmax = 68 кН, то

Построение эпюр нормальных σ и касательных τ напряжений в неблагоприятном сечении балки:

В отношении главных напряжений неблагоприятным является сечение над левой опорой, в котором:

Значение напряжений в различных точках по высоте двутавра сведены в таблицу 1

Проверка прочности балки по главным напряжениям

Наиболее опасной точкой в неблагоприятном сечении является точка 3. В этой точке σ 1=118 МПа и σ 3= -16 МПа. Проверяем прочность в этой точке по третьей гипотезе прочности согласно неравенству σ 1 — σ 3≤ [ σ ].

Так как 118 — ( -16) = 134 θ

откуда θ = -8,48∙10 -3 радиан.

Прогиб в пролете при z=l/2=4/2=2 м.

Аналогично определяется прогиб на конце консоли при z = l + a =4+0,8 = 4,8 м.